前言：

本篇博客会带你理解面对二叉树题型时的两种解题思维模式：（我先总结出来，不理解往下看）
1、是否可以通过遍历一遍二叉树得到答案？
如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。（就是根据当前节点的值来进行处理操作，可以得出答案）。
2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？
如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。（就是将问题分解为左右子树的问题，看看是否通过对左右子树进行处理可以得出答案）
但是无论使用哪种思维模式，你都需要思考：
如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？ 其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

🐕啥叫“框架思维”

先解释一下啥叫“框架思维”，就是看到一道算法题，你下意识的就想到用什么方法，甚至还没有仔细看题目限制条件，就可以基本将70%的代码写出来，剩下没写的就是限制条件。
（举个例子：就是英语考试的作文题，如果你有一套写作框架/模板（就是你背的英语作文模板）,就能很快的完成一篇英语作文）

🏨深入理解前中后序

我们学习二叉树时，都学过前序遍历、中序遍历、后序遍历，先来回顾一下，找一下区别吧

是不是分别在前序位置、中序位置、后序位置上呢？那么它们的位置不同，产生的作用也不同。
如果你意识到了这一点，证明你已经理解了它们作用不一样。

🪀前序位置与后序位置区别

你也注意到了，只要是递归形式的遍历（数组也能递归），都可以有前序位置和后序位置，分别在递归之前和递归之后.
所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同：

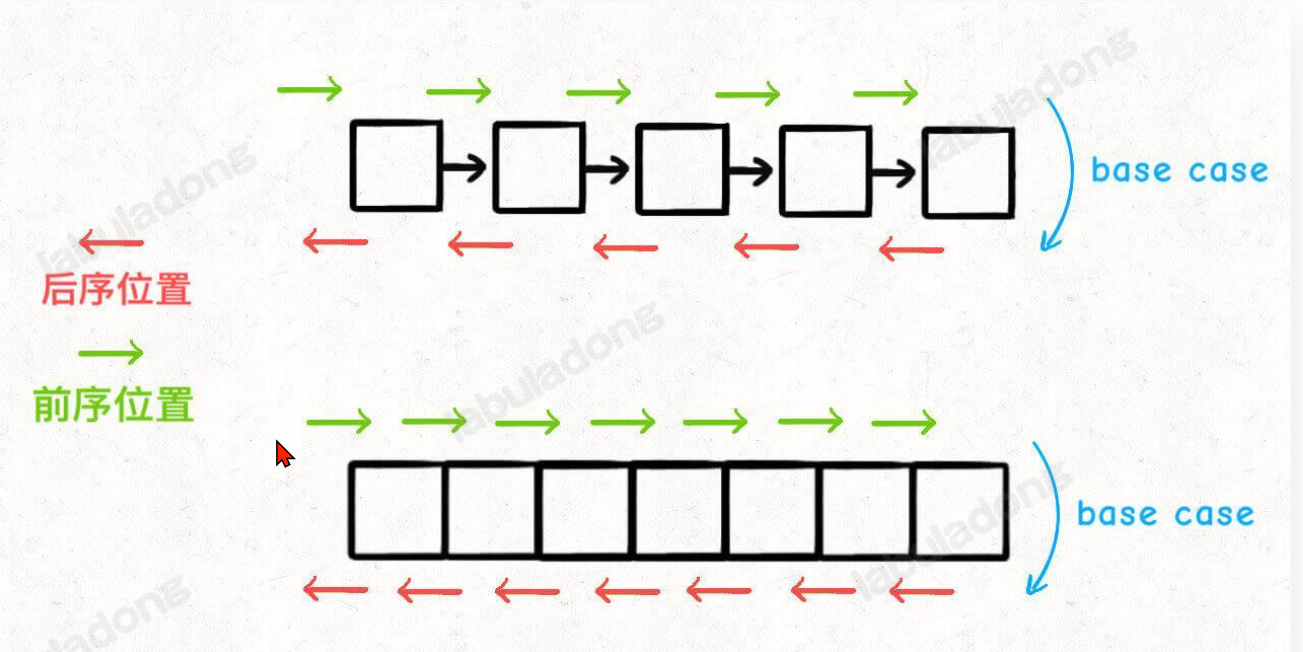
🎀下面以一个链表入手，让你理解前序位置与后序位置的区别，而二叉树无非是多了一个中序位置而已。

思考：如何倒序打印链表呢？如何正序打印链表呢

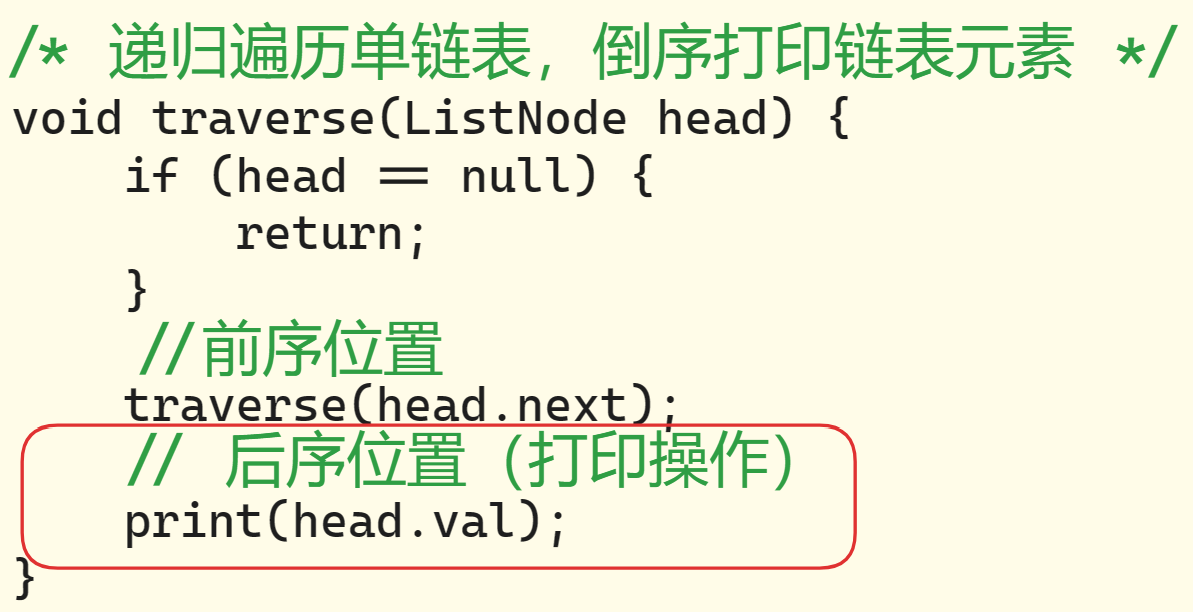
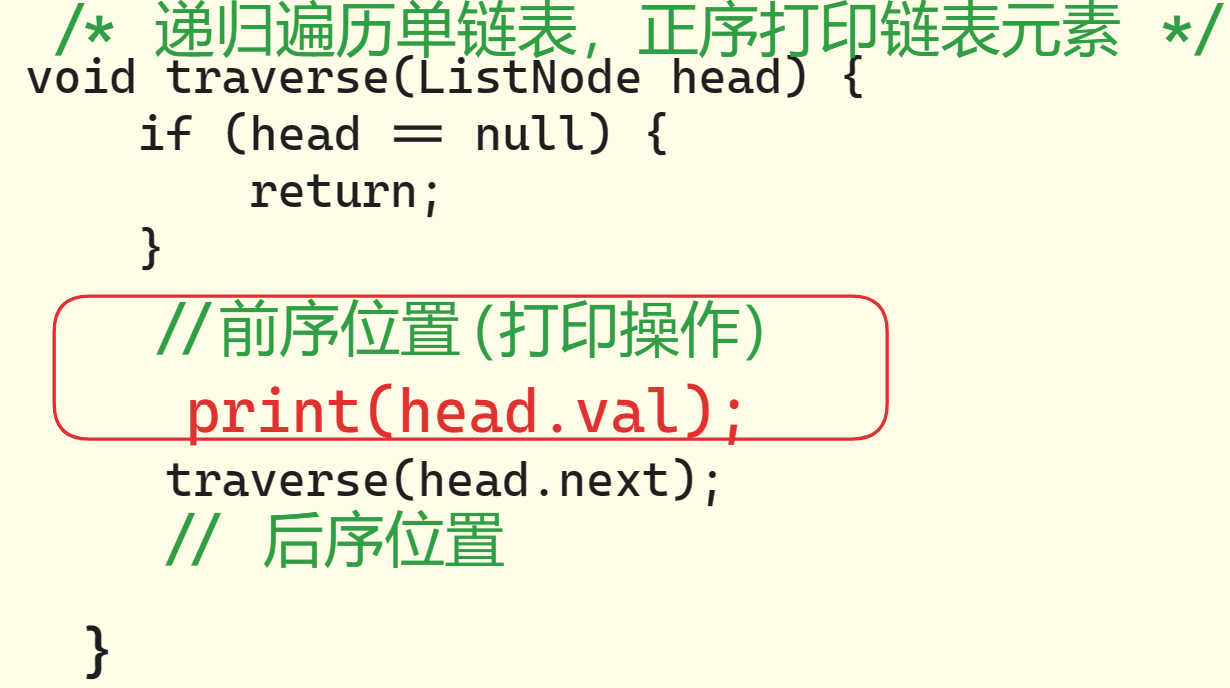
看到这里，你是否对这张图中内容理解了呢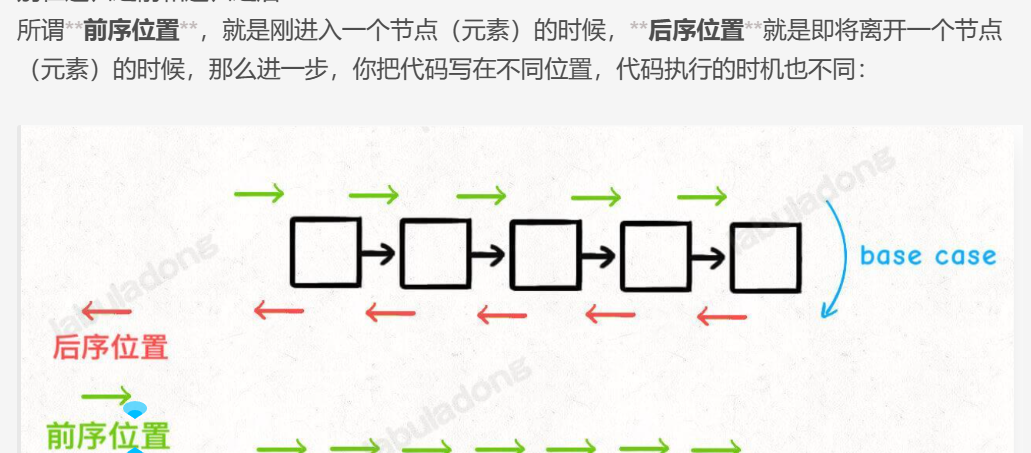
那么说回二叉树也是一样的，只不过多了一个中序位置罢了。
教科书里只会问你前中后序遍历结果分别是什么，所以对于一个只上过大学数据结构课程的人来说，他大概以为二叉树的前中后序只不过对应三种顺序不同的 List<Integer> 列表。
但是我想说，前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：

前序位置的代码在刚刚进入一个二叉树节点的时候执行；

后序位置的代码在将要离开一个二叉树节点的时候执行；

中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

你注意本文的用词，我一直说前中后序「位置」，就是要和大家常说的前中后序「遍历」有所区别：
你可以在前序位置写代码往一个 List 里面塞元素，那最后得到的就是前序遍历结果；但并不是说你就不可以写更复杂的代码做更复杂的事。
画成图，前中后序三个位置在二叉树上是这样：

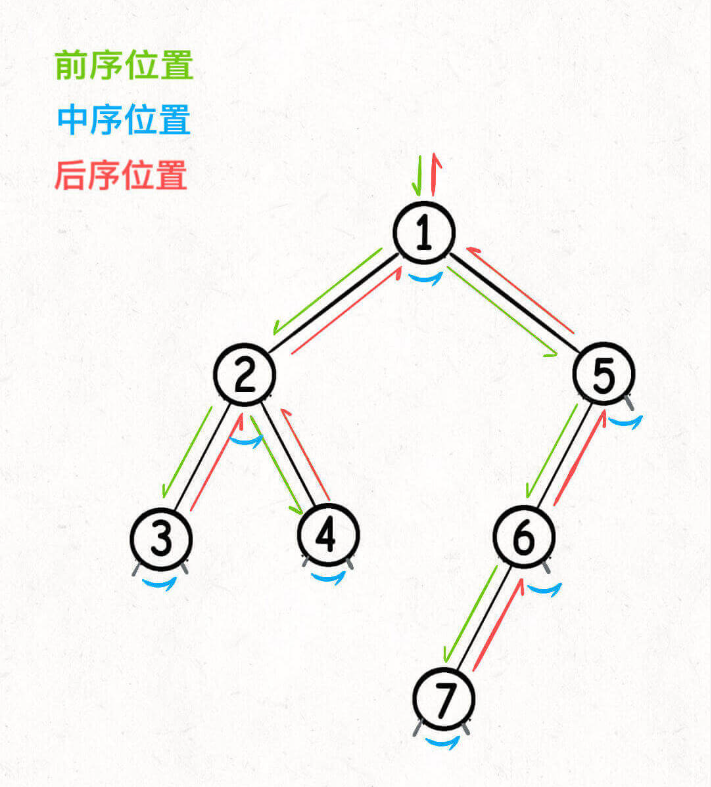
你可以发现每个节点都有「唯一」属于自己的前中后序位置，所以其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

两种解题思路：

二叉树题目的递归解法可以分两类思路，（无论题目是简单困难）

• 第一类是遍历一遍二叉树得出答案，
• 第二类是通过分解成左右子树问题计算出答案

下面用几道简单题来练习一下：

力扣 104.二叉树的最大深度

🎀力扣 104.二叉树的最大深度

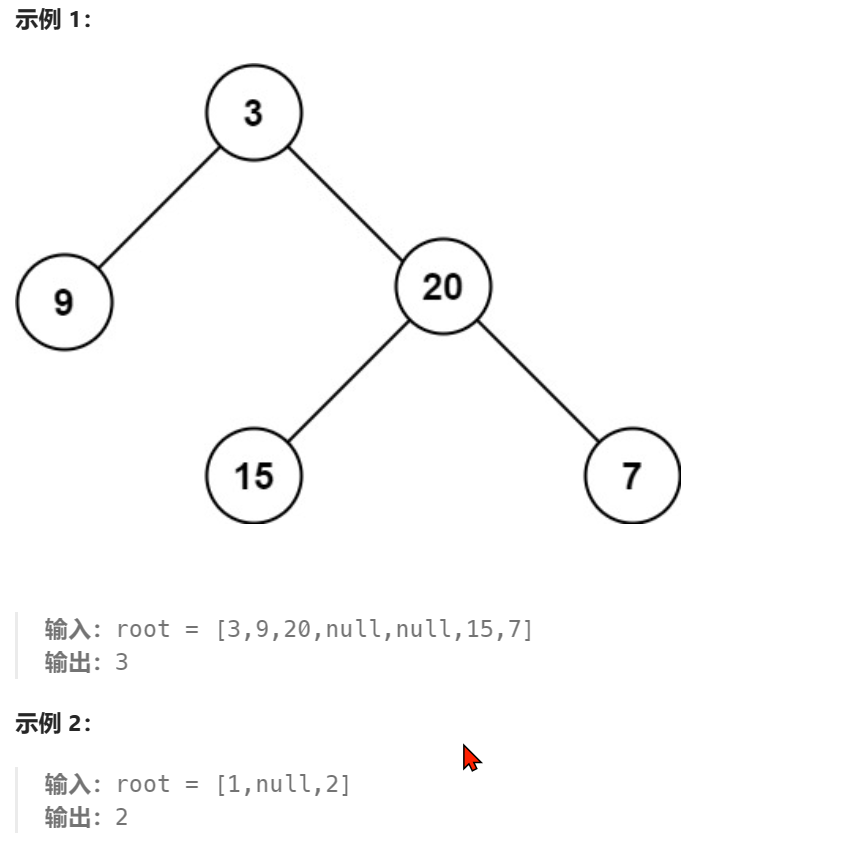
给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
提示：

• 树中节点的数量在 [0, 104] 区间内。
  -100 <= Node.val <= 100

🏅解法一能否利用分解为左右子树来推出结果

  public int maxDepth(TreeNode root) {
  //思路：能否利用遍历一次二叉树解决问题？可以，【前序位置，当前进入时++，后序位置，回溯退出时--】
        //思路：能否利用分解为左右子树来推出结果？可以，【后序位置】
        //思路2：
        if(root==null){
            return 0;
        }
        int leftDepth = maxDepth(root.left);//获取左子树的最大深度
        int rightDepth = maxDepth(root.right);//获取右子树的最大深度
        return Math.max(leftDepth,rightDepth)+1;
    }

🏅解法二能否利用遍历一次二叉树解决问题

 public int maxDepth(TreeNode root) {
        //思路：能否利用遍历一次二叉树解决问题？可以，【前序位置，当前进入时++，后序位置，回溯退出时--】
        //思路：能否利用分解为左右子树来推出结果？可以，【后序位置】
        //思路1：
        if(root==null){
            return 0;
        }
        maxDepth++;//进入当前节点
        maxDepth(root.left);//进入左子树
        res=Math.max(res,maxDepth);
        maxDepth(root.right);//进入右子树
        maxDepth--;//从右子树回溯到当前节点，深度-1
        return res;
    }

力扣 144.翻转二叉树

🎀力扣 144.翻转二叉树

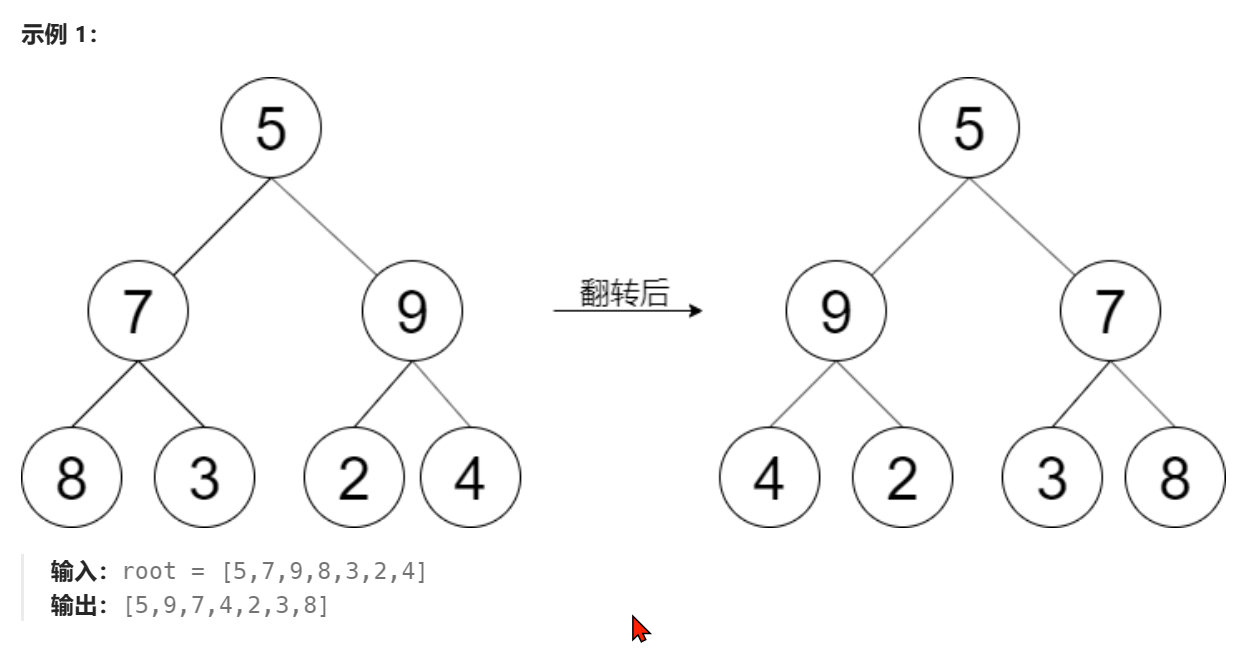
给定一棵二叉树的根节点 root，请左右翻转这棵二叉树，并返回其根节点。

提示：

• 树中节点的数量在 [0, 100] 区间内。
  -100 <= Node.val <= 100

🏅解法一能否利用分解为左右子树来推出结果

 public TreeNode mirrorTree(TreeNode root) {
        //思路：是否能通过分解左右子树来解决问题
        
        if(root==null){
            return root;
        }
        TreeNode left= mirrorTree(root.left);
        TreeNode right= mirrorTree(root.right);
        //后序位置
        root.left=right;
        root.right=left;
        return root;
    }

🏅解法二能否利用遍历一次二叉树解决问题

public TreeNode mirrorTree(TreeNode root) {
        //思路:是否能通过一次二叉树遍历推出结果呢？可以
        if(root==null){
            return root;
        }
        //前序位置
        TreeNode temp=root.left;//先寄存当前节点的左子树
        root.left=root.right;
        root.right=temp;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }