二阶RC低通滤波器

二阶RC低通滤波器是一种常用的电路，用于滤除输入信号中高频部分，只保留低频部分。

一、原理

二阶RC低通滤波器由两个电阻（R1, R2）和两个电容（C1, C2）组成，他们的原理基于RC电路的特性，通过选择合适的电阻和电容值，可以实现对不同频率信号的滤波。

在二阶RC低通滤波器中，输入信号经过第一个电阻R1后，与第一个电容C1相连，形成一个一阶低通滤波器。该一阶低通滤波器的截止频率为：

$$f_{c}1=1/(2\pi R_1{C}_1)$$

输出信号经过第二个电阻R2后，与第二个电容C2相连，形成第二个一阶低通滤波器。该一阶低通滤波器的截止频率为：

$$f_{c}2=1/(2\pi R_2{C}_2)$$

二阶RC低通滤波器的总截止频率为：

$$f_c=1/(2\pi \sqrt{R_1{R}_2{C}_1{C}_2})$$

二、应用

二阶RC低通滤波器广泛应用于电子设备中。以下是一些常见的应用场景∶

1. 音频处理∶在音频设备中，二阶RC低通滤波器可以用于滤除高频噪声，保留音频信号的低频部分，使音质更清晰。
2. 通信系统∶在无线通信系统中，二阶RC低通滤波器可以用于滤除高频干扰信号，提高信号的质量和稳定性。
3. 功率电子∶在功率电子领域中，二阶RC低通滤波器可以用于平滑直流电压或电流信号，减小电压或电流的纹波。
4. 传感器信号处理:在传感器应用中，二阶RC低通滤波器可以用于滤除传感器信号中的高频噪声，提取出有效的信号信息。

二阶RC带通滤波器

带通滤波器可用于隔离或滤除位于特定频带或频率范围内的某些频率。简单的RC无源滤波器中的截止频率或ƒc点可以通过仅使用一个与无极性电容器串联的电阻器来精确控制，并且根据连接它们的方式，我们可以看到低通或获得高通滤波器。

通过将单个低通滤波器电路与高通滤波器电路连接或“级联” ，我们可以生产另一种无源RC滤波器，该滤波器通过选定的范围或“频带”，该频带可以窄或宽，同时衰减所有超出此范围的人。这种新型的无源滤波器装置可产生一个频率选择滤波器，通常称为带通滤波器或简称BPF。

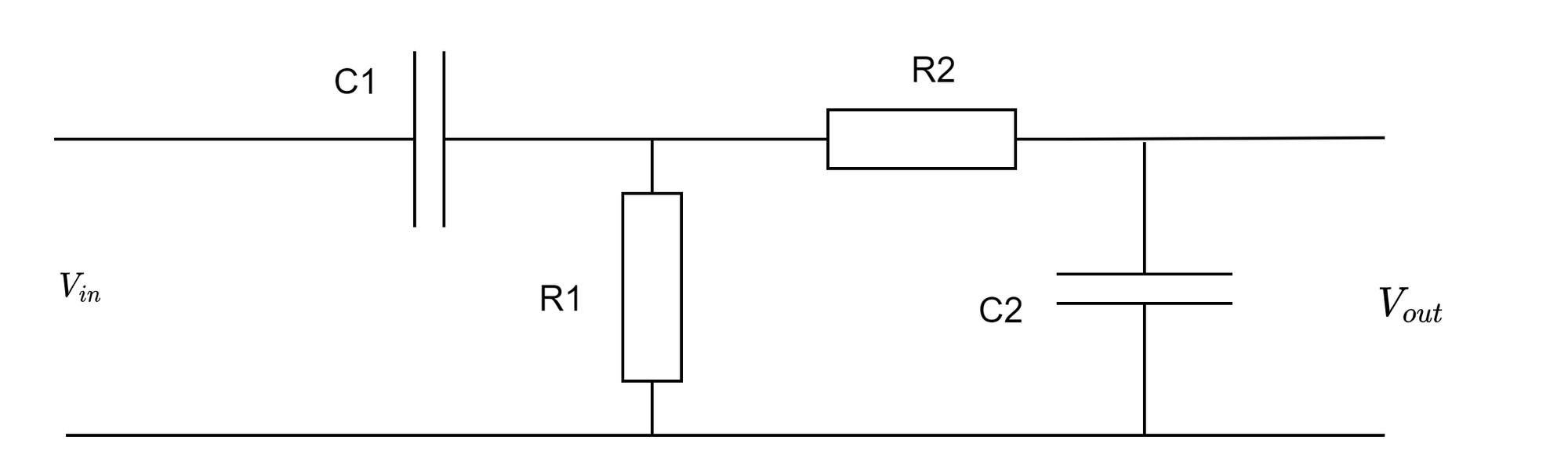
可以使用与低通和高通滤波器相同的公式找到带通滤波器的上限和下限截止频率点。

$$f_c=1/(2\pi RC)$$

那么显然，可以通过两个滤波器的两个截止频率点的位置来控制滤波器的通带宽度。

将使用RC组件构建一个二阶带通滤波器，该滤波器将仅允许一定范围的频率通过高于1kHz（1,000Hz）和低于30kHz（30,000Hz）的频率。假设两个电阻的阻值为10kΩ，则计算所需的两个电容的阻值。

高通滤波器阶段

截止频率ƒ为1kHz时，电阻值10kΩ，电容C1的计算公式为：

$$C_1=1/(2\pi f_{L}R)=\frac{1}{2\pi \times 1000\times 10000}=15.9nF$$

低通滤波器阶段

截止频率ƒ 为30kHz，电阻值10kΩ时，电容C2的计算公式为：

$$C_2=1/(2\pi f_{H}R)=\frac{1}{2\pi \times 30000\times 10000}=530pF$$

带通滤波器谐振频率

还可以计算输出增益达到最大值或峰值时带通滤波器的“谐振”或“中心频率”（$f_r$）点。该峰值不是可能期望的-3dB上下截止点的算术平均值，而是实际上的“几何”或平均值。

中心频率方程

$$f_r=\sqrt{f_L\times f_H}$$

其中，$f_r$是谐振或中心频率

$f_L$ 是下-3dB截止频率点

$f_H$是上部-3db截止频率点