【牛客面试必刷TOP101】Day8.BM33 二叉树的镜像和BM36 判断是不是平衡二叉树

news2024/11/24 8:27:10

作者简介：大家好，我是未央；

博客首页：未央.303

系列专栏：牛客面试必刷TOP101

每日一句：人的一生，可以有所作为的时机只有一次，那就是现在！！！！！

文章目录

前言

一、二叉树的镜像

题目描述

题目解析

二、判断是不是平衡二叉树

题目描述

题目解析：

总结

前言

一、二叉树的镜像

题目描述

描述：
操作给定的二叉树，将其变换为源二叉树的镜像。

数据范围：二叉树的节点数 0≤n≤1000 ，二叉树每个节点的值 0≤val≤1000；

要求：空间复杂度 O(n) 。本题也有原地操作，即空间复杂度O(1) 的解法，时间复杂度 O(n)

举例说明：

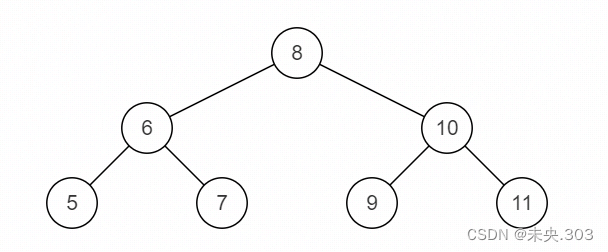
源二叉树：

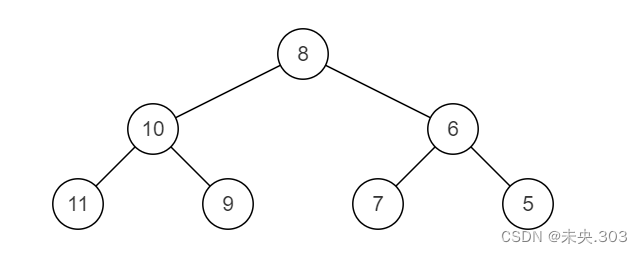
镜像二叉树：

示例1：

示例2：

题目解析

题目的主要信息：

将二叉树镜像，即将其所有左右子树交换

我们可以考虑自底向上依次交换二叉树的左右节点。

解题思路：

因为我们需要将二叉树镜像，意味着每个左右子树都会交换位置，如果我们从上到下对遍历到的节点交换位置，但是它们后面的节点无法跟着他们一起被交换，因此我们可以考虑自底向上对每两个相对位置的节点交换位置，这样往上各个子树也会被交换位置。

自底向上的遍历方式，我们可以采用后序递归的方法。

解题步骤：

step 1：先深度最左端的节点，遇到空树返回，处理最左端的两个子节点交换位置。
step 2：然后进入右子树，继续按照先左后右再回中的方式访问。
step 3：再返回到父问题，交换父问题两个子节点的值。

代码编写：

二、判断是不是平衡二叉树

题目描述

描述：

输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。

平衡二叉树的定义：

可定义为或者是一棵空树，

或者是具有下列性质的二叉树：

1.左子树和右子树均为平衡二叉树；

2.左子树和右子树的高度差的绝对值不超过1。

注意：平衡二叉树一定是二叉排序树。含有n个结点的平衡二叉树的最大深度为O(log2(n))，即平衡二叉树的平均查找长度为O(log2(n))。

举例说明:
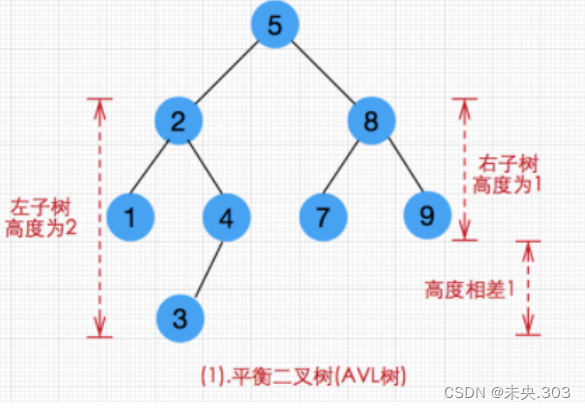
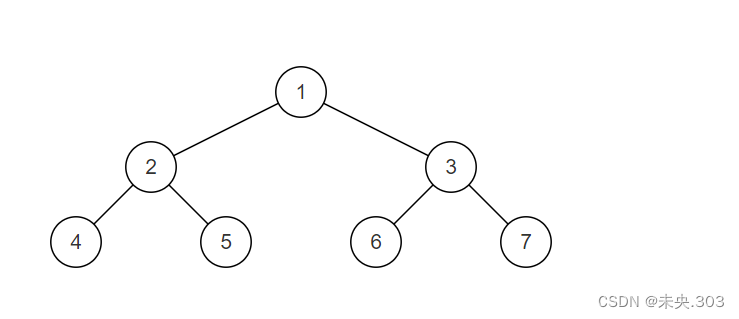
平衡二叉树:

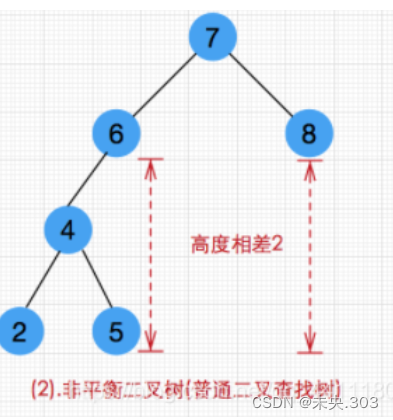
非平衡二叉树：

样例解释：

样例二叉树如图，为一颗平衡二叉树

注：我们约定空树是平衡二叉树。

数据范围：n≤100,树上节点的val值满足 0≤n≤1000；

要求：空间复杂度O(1)，时间复杂度 O(n)；

输入描述：

输入一棵二叉树的根节点;

返回值描述：

输出一个布尔类型的值;

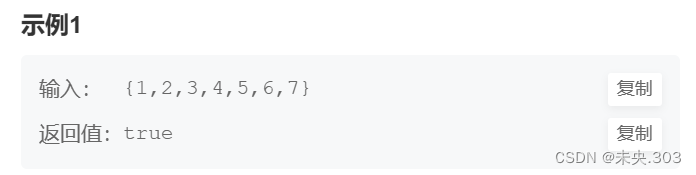
示例1：

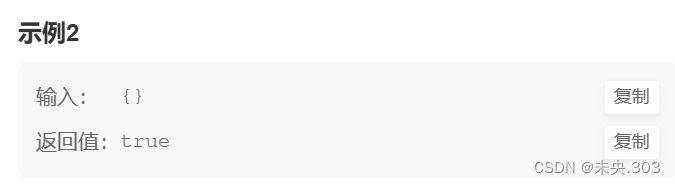
示例2：

题目解析：

从题中给出的有效信息：

左右两个子树的高度差的绝对值不超过1
左右两个子树都是一棵平衡二叉树

故此首先想到的方法是使用递归的方式判断子节点的状态；

解题思路：

平衡二叉树任意节点两边的子树深度相差绝对值不会超过1，且每个子树都满足这个条件，那我们可以对每个节点找到两边的深度以后：

判断是否两边相差绝对值超过1：

然后因为每个子树都满足这个条件，我们还需要遍历二叉树每个节点当成一棵子树进行判断，而对于每个每个节点判断后，其子节点就是子问题，因此可以用递归。

IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);

解题步骤：

step 1：第一个函数递归遍历二叉树所有节点。
step 2：对于每个节点判断，调用第二个函数获取子树深度。
step 3：第二个函数递归获取子树深度，只需要不断往子节点深度遍历，累加左右深度的较大值。
step 4：根据深度判断该节点下的子树是否为平衡二叉树。