图源:文心一言
本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝
- 第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武忠祥
📇目录
📇目录
🦮思维导图
🐳向量代数
🐋数量积【数字】
🐋向量积【向量】
🐋混合积【数字】
🐳空间解析几何
🐋平面空间与直线
🐋曲面与空间曲线
🐳积分学的几何应用
🐋单积分、二重积分
🐋三重积分
🐋曲线积分
🐋曲面积分
🐋多元积分应用
🐳场论初步
🔚结语
🦮思维导图

- 🌸思维导图为整理武老师基础教材所列内容,时间关系有些仓促,请多包涵~
- 🌸博文后面会以大纲的形式复述一遍,面向复习,不会写得很详细,且可能有误;较为重要的内容有从网络找相关配图并给出大佬博文链接~
-
🐳向量代数
-
🐋数量积【数字】
- 几何表示:
- 代数表示:
- 几何应用
- 求夹角
- 判定垂直
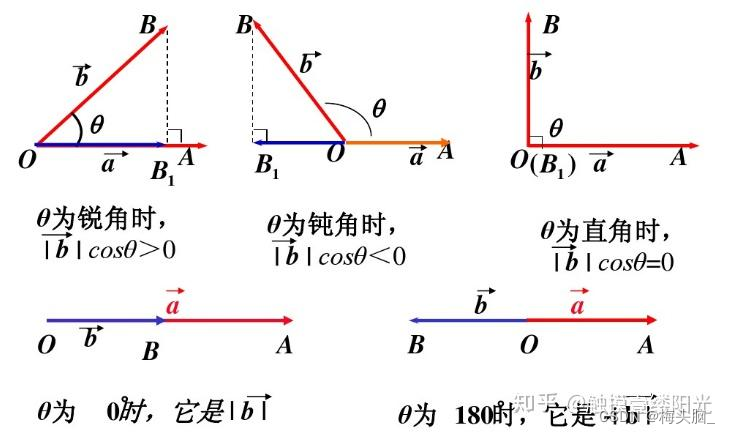
图源:线性代数~数量积 - 知乎
- 几何表示:
-
🐋向量积【向量】
- 几何表示
- 模:
- 方向:右手法则
- 模:
- 代数表示:矩阵【首行基坐标,次行向量a的分量,尾行向量b的分量】

图源:向量外积的坐标形式_向量外积的坐标表示-CSDN博客
- 运算规律:
【模不变,方向相反】
- 几何应用
- 求同时垂直于 a 和 b 的向量
- 判定平行
- 求以a和b为邻边的平行四边形的面积
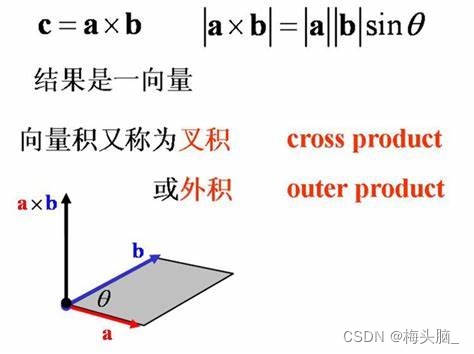
图源:向量的数量积与向量积 - 童趣PBL
- 几何表示
-
🐋混合积【数字】
- 几何表示:
- 代数表示:矩阵【首行向量a的分量,次行向量b的分量,尾行向量c的分量】
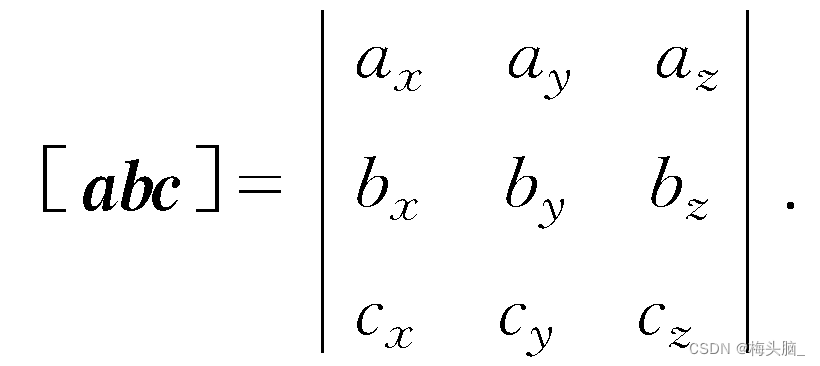
图源:1272. 如何计算混合积?-高等数学-专业词典
- 运算规律
- 轮换对称性:
- 交换变号:
- 原理:矩阵交换1次行列变正负号
- 轮换对称性:
- 几何应用
- 求以a、b、c为邻边的平行六边体的面积
- 求向量共面:(abc)=0【等式中任意两个向量平行,则3个向量必共面】
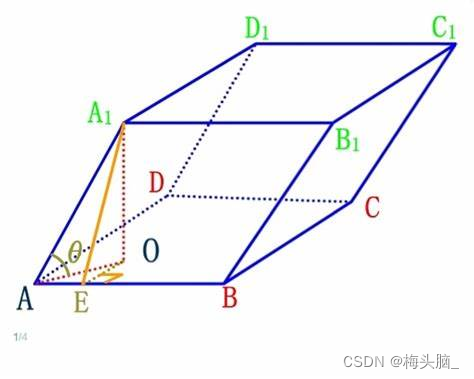
图源:混合积的几何意义
- 几何表示:
-
-
🐳空间解析几何
-
🐋平面空间与直线
- 概要
- 平面方程
- 一般式:
- 点法式:平面上1点(x0,y0,z0)和法线向量(A,B,C)表示直线
- 截距式:经过坐标轴的3个交点表示平面
图源:平面方程_百度百科 (baidu.com)
- 一般式:
- 直线方程
- 一般式:2个平面的交线表示直线
- 对称式:直线上1点(x0,y0,z0)和方向向量(l,m,n)表示直线
- 参数式:直线上1点(x0,y0,z0)和方向向量(l,m,n)表示直线
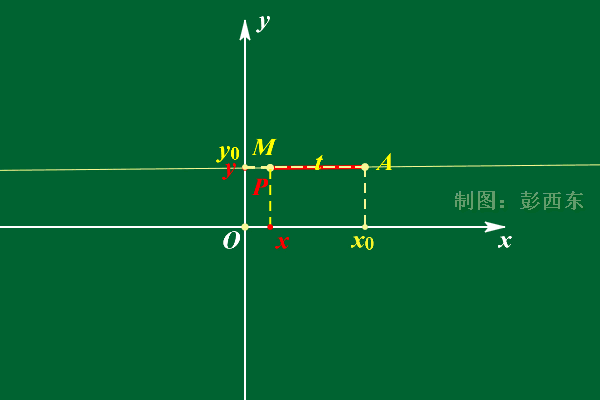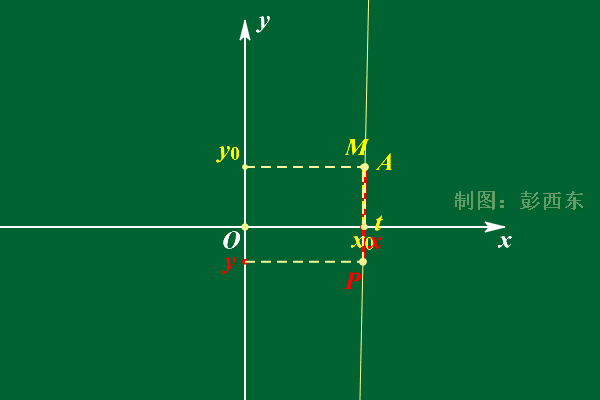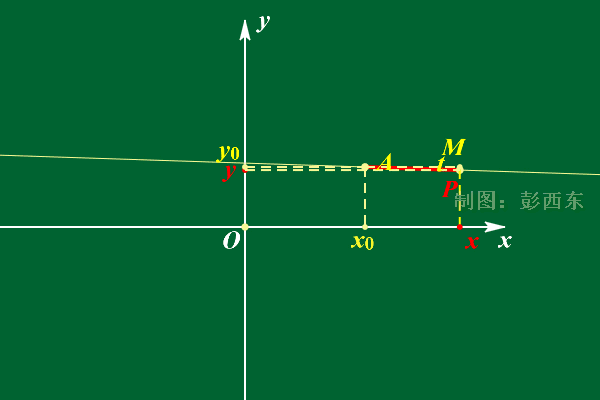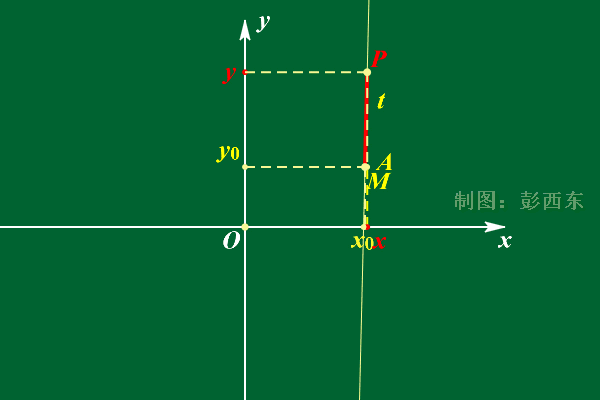
图源:不可不知的——直线的参数方程 (qq.com)
- 一般式:2个平面的交线表示直线
- 点到平面的距离
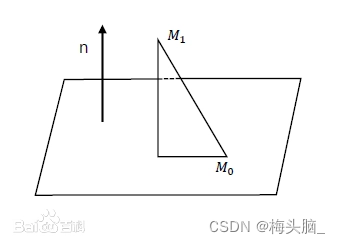
距离为M1M0在平面法向量的投影长度:
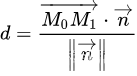
代入点,M1与MO点乘为分子,M0满足平面方程化简,平面法向量的模为分母:
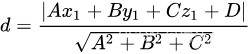
图源:点到平面距离_百度百科 (baidu.com)
- 点到直线的距离
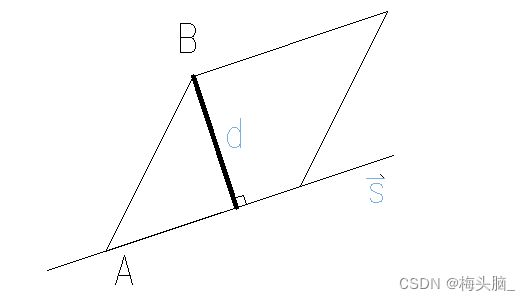
平行四边形满足等式:
代入方向向量S(l,m,n),B(x1,x2,x3),A(x0,y0,z0),得
- 平面方程
- 题型
- 求法向量、切线向量,建立平面与直线的方程
- 求点到直线的距离
- 概要
-
🐋曲面与空间曲线
- 概要
- 曲面方程
-
-
-
- 空间曲线
- 参数式【螺线】

图源:确实没找到...
- 一般式:2个曲面的交线表示空间曲线
- 常见曲面
- 旋转面:平面曲线绕平面直线旋转
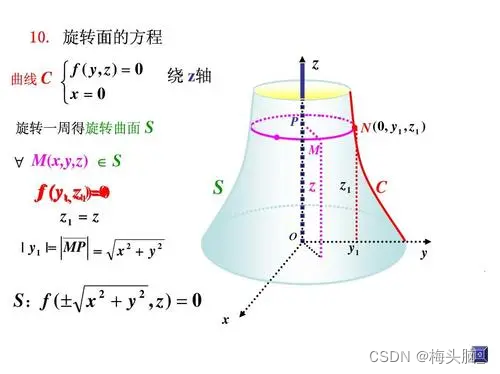
-
柱面:平行与定直线并沿定曲线移动的直线形成的轨迹
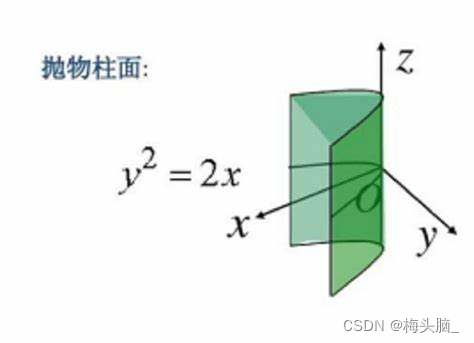
图源:抛物柱面函数 - 快懂百科
- 二次曲面
- 圆柱面
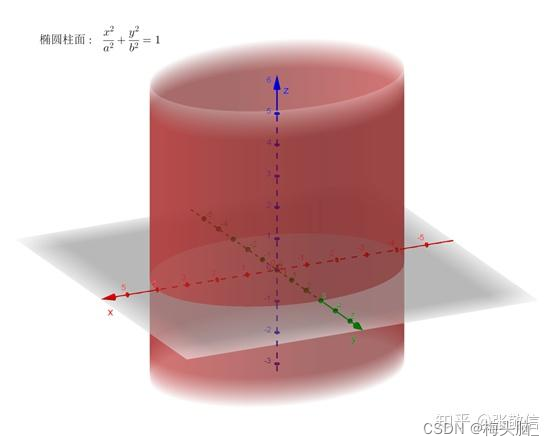
- 圆锥面
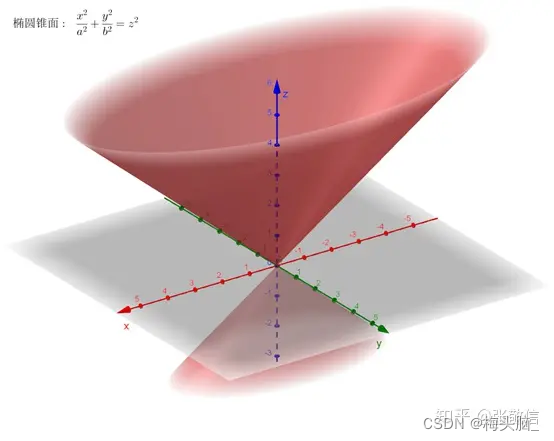
- 旋转抛物面
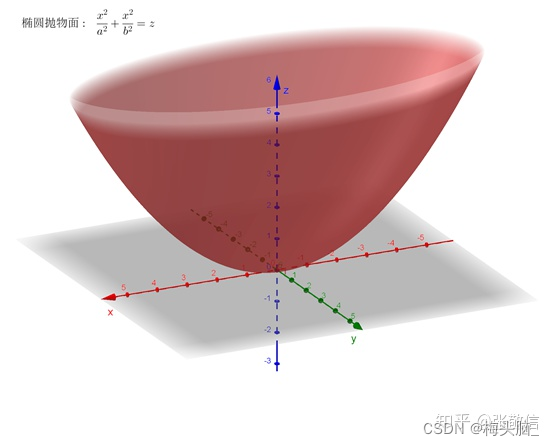
- 椭球面

图源:【高等数学】九种标准二次曲面 - 知乎 (zhihu.com)
- 空间曲线投影
- 投影柱面:曲线一般式联立消去z,得到的二元方程即为母线为z轴的投影柱面
- 投影平面:在投影柱面方程的基础上,增加限制条件 z = 0,检查其它变量的取值范围,即为曲线在xoy面的投影
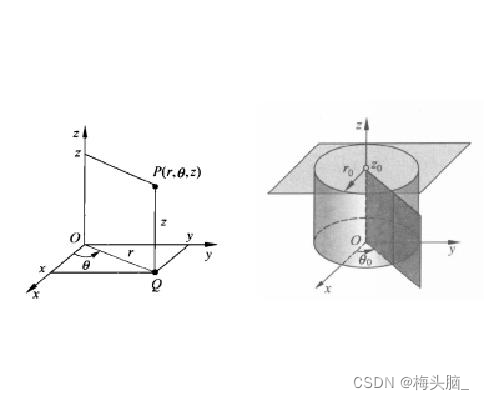
图源:柱面坐标 - 搜狗百科 (sogou.com)
- 旋转面:平面曲线绕平面直线旋转
- 曲面方程
-
题型
- 曲面方程
- 求柱面方程
- 求旋转面方程
- 求投影曲线方程
- 解析几何
- 曲面的切平面与法线,核心:求法向量
- 曲线的切线与法平面,核心:求切向量
- 曲面方程
- 概要
-
-
🐳积分学的几何应用
-
🐋单积分、二重积分
- 概念
- 平面图形的面积
- 直角坐标
- 极坐标
- 直角坐标
- 旋转体体积
- 绕x轴旋转
,其中体积微元
= 底面积
x 高
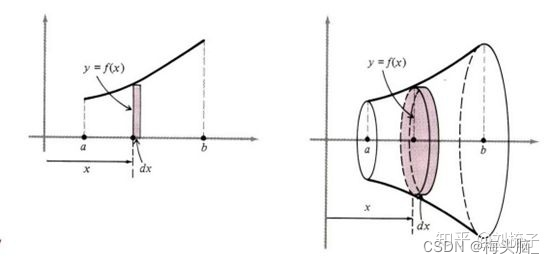
图源:单变量微积分-第十六讲-积分的应用(一) - 知乎
- 绕y轴旋转
,其中体积微元
= 环状窄带周长
x 截面积
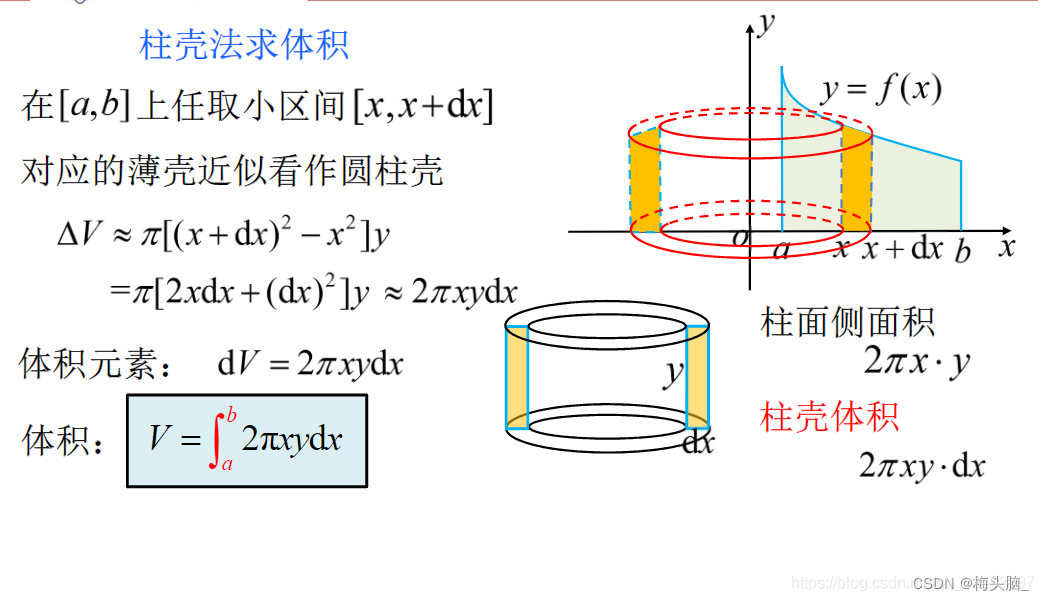
图源:定积分的应用之 柱壳法求旋转体体积_-CSDN博客
- 绕直线旋转
,其中体积微元
= = 环状窄带周长
x 截面积
,
表示点到直线距离
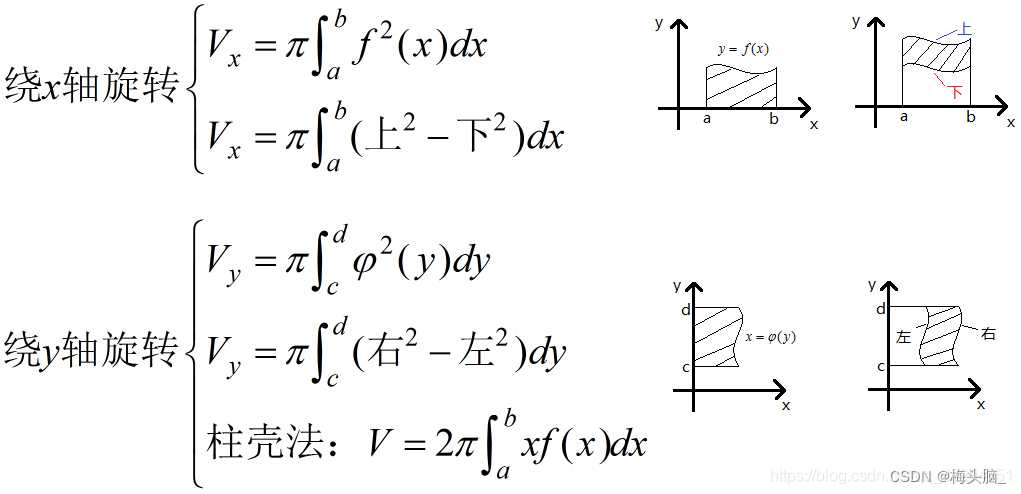
图源:高等数学解题常用公式笔记总结
- 绕x轴旋转
- 曲线弧长:同对弧长的线积分
- 旋转体侧面积
- 绕x轴旋转
,其中面积微元
= 环状窄带周长
x 高度
,

图源:求曲线绕x轴旋转一周的旋转体的侧面积_360问答
- 绕x轴旋转
- 平面图形的面积
- 题型
- 几何应用:
- 定积分求面积
- 绕轴旋转体积
- 物理应用
- 容积 = 底面积 x 高
- 球1底面积
,高度微元
- 球1体积微元
,积分域-1到1/2
- 球1体积
,代入圆的公式
,得
- 球2与球1体积相等,球1体积×2即为所求
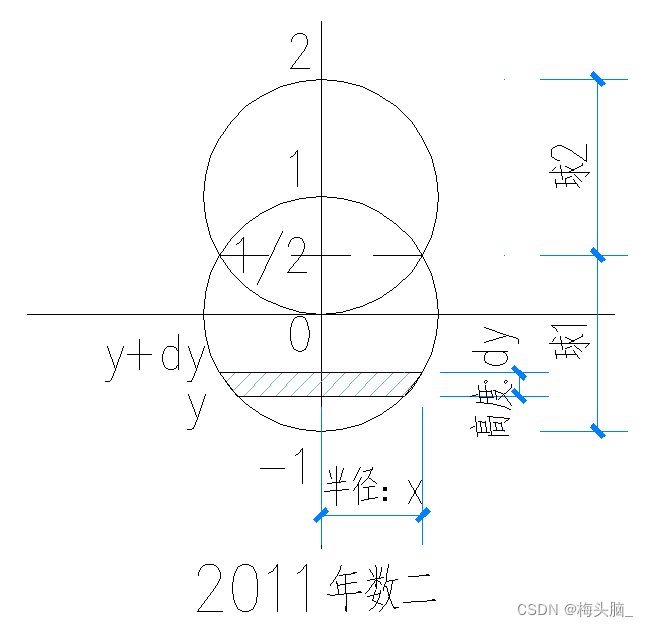
- 球1底面积
- 做功 = 力 x 距离
- 球1受力微元
,距离
;
- 球1做功微元
;
- 以上,球1区域做功
;
- 同理,球2区域做功
;

- 球1受力微元
- 压强 = 压力 x 面积
- 区域1压力:
,区域1面积
;
- 区域1压强微元:
;
- 区域1压强:
;
- 区域2压力:
,区域2面积
;
- 区域2压强微元:
;
- 区域2压强:
;
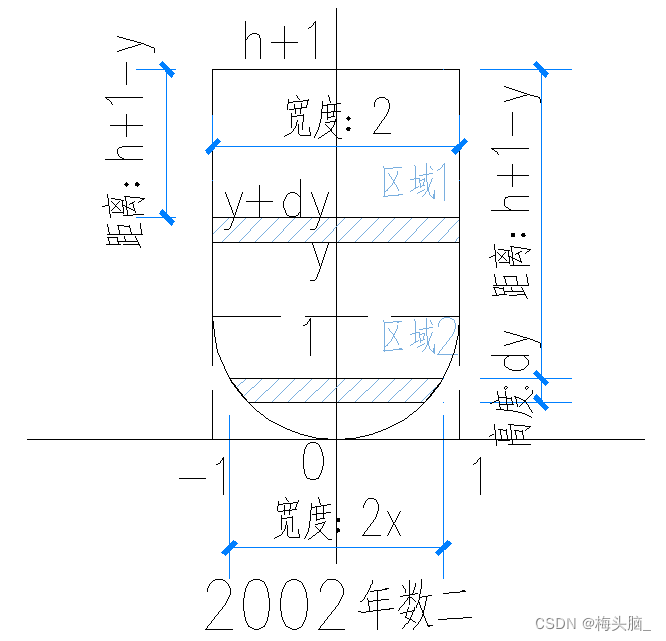
- 区域1压力:
- 容积 = 底面积 x 高
- 几何应用:
- 概念
-
🐋三重积分
- 简述:区域点的函数值 x 体积微元,累加求和
- 性质
- 奇偶性、轮换对称性
- 不等式性质
- 积分中值定理
- 计算
- 先一后二
- 计算
- 作垂直于z轴的直线,穿过封闭底面z1(x,y)与顶面z2(x,y),即z的积分上下限是x,y的函数
- 先计算有关z的积分,再转化为求x,y的二重积分
- 适合坐标
- 印象中比较万能...
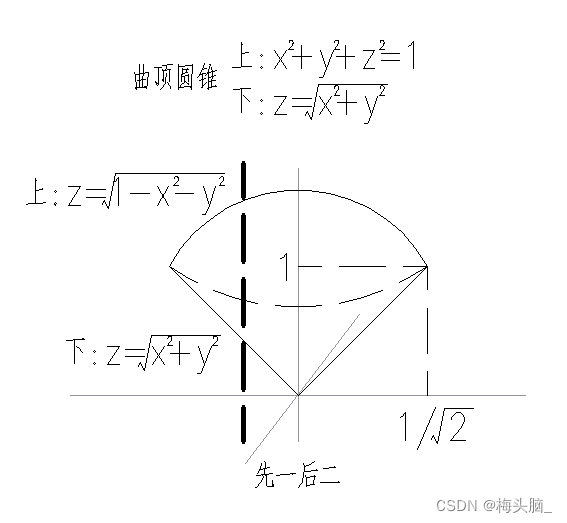
- 计算
- 先二后一
- 计算
- 作平行于z轴的截面,得到封闭曲线,即z的积分上下限是常数
- 先计算有关x,y的二重积分,再转化为求z的单积分
- 适合坐标
- 被积函数:
,这一步可能需要借助奇偶性、对称性转换得到
- 积分域:
面积较为规则,方便计算
- 被积函数:
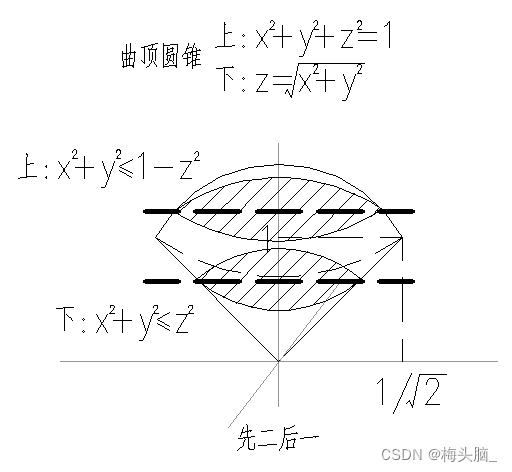
- 计算
- 柱坐标
- 与直角坐标的关系
- 坐标
-
-
-
-
- 体积微元
-
-
- 坐标
- 适合坐标
- 被积函数:
- 积分域:柱面、锥面
- 被积函数:
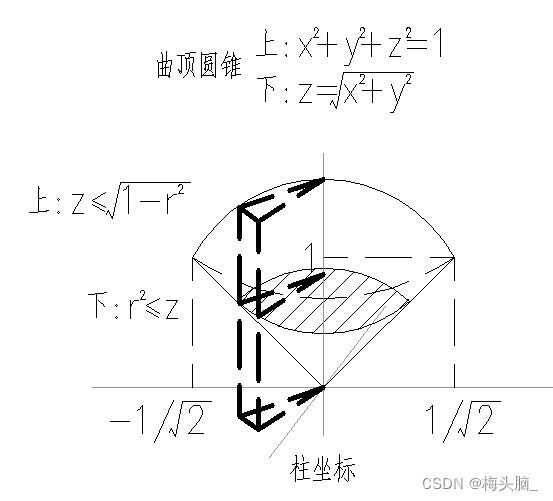
- 与直角坐标的关系
- 球坐标
- 与直角坐标的关系
- 坐标
-
-
-
-
- 体积微元
- 坐标
- 适合坐标
- 被积函数:
- 积分域:球面、球壳、锥面
- 被积函数:
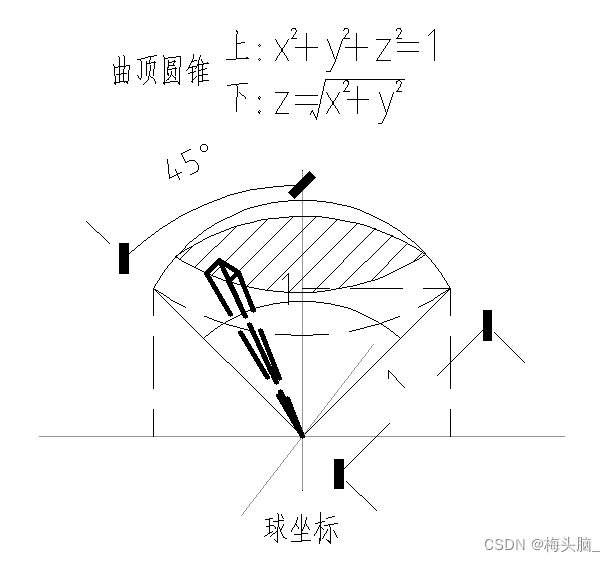
- 与直角坐标的关系
- 先一后二
-
🐋曲线积分
- 对弧长的线积分
- 简述:函数值 x 弧长微元,累加求和
- 计算方法
- 直接法
- 体积微元
- 参数方程:
- 直角坐标:
- 极坐标:
- 参数方程:
- 积分域:从小到大【与方向无关,要求结果是正数】
- 体积微元
- 奇偶性【x轴、y轴】
- 对称性【直线y=x】
- 直接法
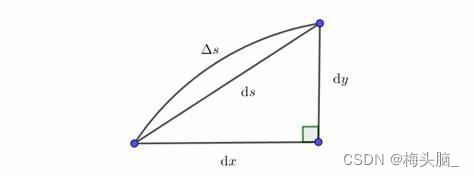
图源:【高等数学】定积分元素法及应用(待续) - 知乎
- 对坐标的线积分
- 简述:函数值 x 有向线段的投影,累加求和
- 计算方法
- 直接法
- 被积函数:代入直角坐标,或极坐标、参数方程
- 积分域:从起点到终点【与方向有关,逆时针为正向】
- 格林公式
- 要求
- 闭区域由分段光滑曲线围成
- 被积函数在积分域上有一节连续偏导数
- 作用:平面坐标的线积分转化为二重积分
- 要求
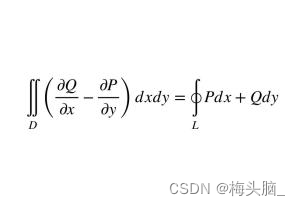
图源:格林公式 - 搜狗百科
- 斯托克斯公式
- 要求
- 闭区域由空间分段光滑曲线围成,方向符合右手法则
- 被积函数在积分域上有一节连续偏导数
- 作用:空间坐标的线积分转化为二重积分
- 要求

图源:斯托克斯公式的意义? - 知乎
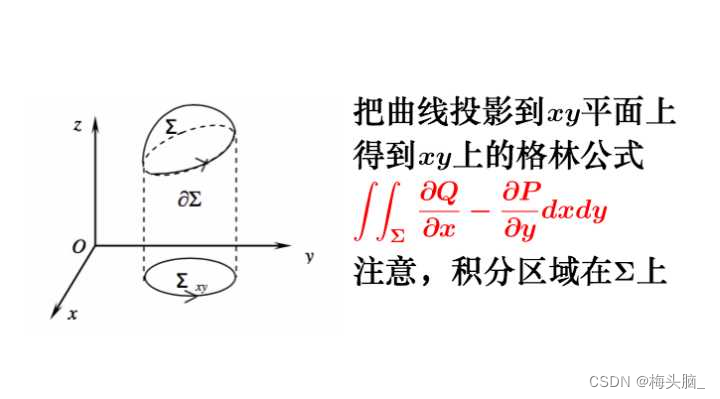
图源:怎么记住斯托克斯公式(Stokes' theorem)? - 知乎
- 直接法
- 方法选择
- 曲线L是否封闭?
- 是:格林【平面】/ 斯托克斯【空间】
- 否:是否与路径无关?
- 是
- 改换路径【一般选择平行坐标轴】
- 寻找原函数【偏积分、凑微分】
- 否
- 直接法【注意方向】
- 补线使用公式
- 是
- 曲线L是否封闭?
- 两类线积分的关系
- 对弧长的线积分 x 曲线在切线方向的余弦 = 对坐标的线积分

图源:多元微积分—— 知乎
- 对弧长的线积分
-
🐋曲面积分
- 对面积的面积分
- 简述:函数值 x 面积微元,累加求和
- 计算方法
- 直接法
- 体积微元:
- 积分域:从小到大【与方向无关,要求结果是正数】
- 体积微元:
- 奇偶性【x轴、y轴】
- 轮换对称性
- 直接法
- 对坐标的面积分
- 简述:函数值 x 有向投影域面积,累加求和
- 计算方法
- 直接法
- 被积函数:代入直角坐标
,或极坐标、参数方程
- 积分域:从起点到终点【与方向有关,上、前、右侧为正向】
- 被积函数:代入直角坐标
- 高斯公式
- 要求
- 闭区域由分段光滑曲线围成
- 被积函数在积分域上有一节连续偏导数
- 作用:空间坐标的面积分转化为三重积分
- 要求
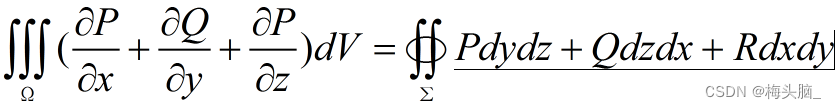
图源:高斯公式 - Bing
- 直接法
- 方法选择
- 曲面是否封闭且不存在奇点?
- 是:高斯公式
- 否
- 直接法【注意方向】
- 补面【不封闭】或作辅助面【存在奇点】使用公式
- 曲面是否封闭且不存在奇点?
- 两类面积分的关系
- 对面积的面积分 x 曲面在切线方向的余弦 = 对坐标的面积分
- 对面积的面积分
-
🐋多元积分应用
- 概要
- 平板面【二重积分】
- 面积
- 被积函数:1
- 质量
- 被积函数:
- 被积函数:
- 质心
- 被积函数:
- 被积函数:
- 转动惯量
- 被积函数:
【对y轴】
- 被积函数:
- 面积
- 推广
- 空间体【三重积分】
- 曲线【一型线积分】
- 曲面【一型面积分】
- 变力做功【二型线积分】
- 通量【二型面积分】
- 平板面【二重积分】
- 题型
- 形心
- 质心
- 变力做功
- 概要
-
-
🐳场论初步
- 方向导数:函数在某点对指定方向求导的结果
- 梯度:函数在这点方向导数最大的方向
- 散度:向量场在某点吸收或散发通量的大小
- 旋度:向量场对某点微元造成的旋转程度
详见大佬博文【我实在是打不动公式了...🫠】微积分-13.场论初步 - 知乎 (zhihu.com)
🔚结语
😶🌫️博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容~
🌟博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,博主肝文的动力++~
🌸博主可能会佛系更新思维导图,在这里:
高等数学_梅头脑_的博客-CSDN博客![]() https://blog.csdn.net/weixin_42789937/category_12380893.html
https://blog.csdn.net/weixin_42789937/category_12380893.html




![[42000][923] ORA-00923: 未找到要求的 FROM 关键字](https://img-blog.csdnimg.cn/29265a741c2e4ca1bd057d527b2495d6.png)