看过来看过去,唯有此up主,非常牛:
Video Explaination(Chinese)
1. DDPM Introduction
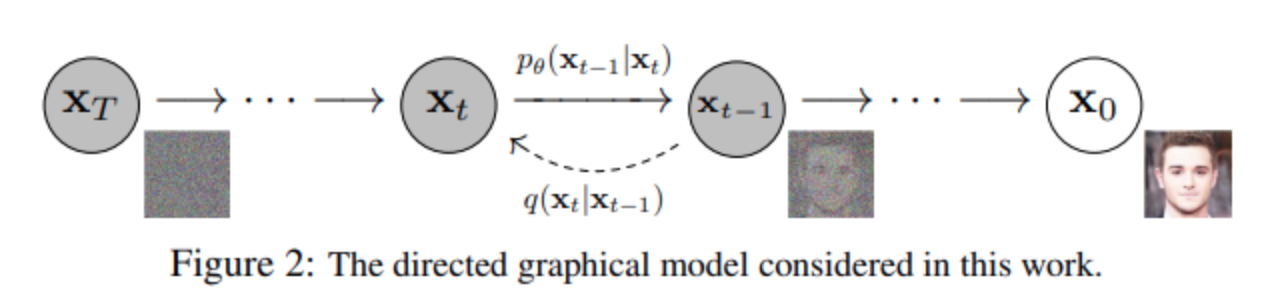
q q q - 一个固定(或预定义)的正向扩散过程,逐渐向图像添加高斯噪声,直到最终得到纯噪声。
p θ p_θ pθ - 一个学习到的反向去噪扩散过程,其中神经网络被训练以逐渐去噪图像,从纯噪声开始,直到最终得到实际图像。
正向和反向过程都由 t t t索引,发生在有限时间步数 T T T内(DDPM的作者使用 T T T=1000)。您从 t = 0 t=0 t=0开始,从数据分布中采样一个真实图像 x 0 x_0 x0,正向过程在每个时间步 t t t中从高斯分布中采样一些噪声,然后将其添加到前一个时间步的图像上。在足够大的 T T T和每个时间步添加噪声的良好安排下,通过逐渐的过程,最终在 t = T t=T t=T处得到所谓的各向同性高斯分布。
2. Forward Process q q q
这个过程是一个马尔可夫链, x t x_t xt 只依赖于 x t − 1 x_{t-1} xt−1。 q ( x t ∣ x t − 1 ) q(x_{t} | x_{t-1}) q(xt∣xt−1) 在每个时间步 t t t 按照已知的方差计划 β t β_{t} βt 添加高斯噪声。
x 0 → q ( x 1 ∣ x 0 ) x 1 → q ( x 2 ∣ x 1 ) x 2 → ⋯ → x T − 1 → q ( x t ∣ x t − 1 ) x T x_0 \overset{q(x_1 | x_0)}{\rightarrow} x_1 \overset{q(x_2 | x_1)}{\rightarrow} x_2 \rightarrow \dots \rightarrow x_{T-1} \overset{q(x_{t} | x_{t-1})}{\rightarrow} x_T x0→q(x1∣x0)x1→q(x2∣x1)x2→⋯→xT−1→q(xt∣xt−1)xT
x t = 1 − β t × x t − 1 + β t × ϵ t x_t = \sqrt{1-β_t}\times x_{t-1} + \sqrt{β_t}\times ϵ_{t} xt=1−βt×xt−1+βt×ϵt
- β t β_t βt is not constant at each time step t t t. In fact one defines a so-called “variance schedule”, which can be linear, quadratic, cosine, etc.
0 < β 1 < β 2 < β 3 < ⋯ < β T < 1 0 < β_1 < β_2 < β_3 < \dots < β_T < 1 0<β1<β2<β3<⋯<βT<1
- ϵ t ϵ_{t} ϵt Gaussian noise, sampled from standard normal distribution.
x t = 1 − β t × x t − 1 + β t × ϵ t x_t = \sqrt{1-β_t}\times x_{t-1} + \sqrt{β_t} \times ϵ_{t} xt=1−βt×xt−1+βt×ϵt
Define a t = 1 − β t a_t = 1 - β_t at=1−βt
x t = a t × x t − 1 + 1 − a t × ϵ t x_t = \sqrt{a_{t}}\times x_{t-1} + \sqrt{1-a_t} \times ϵ_{t} xt=at×xt−1+1−at×ϵt
2.1 Relationship between x t x_t xt and x t − 2 x_{t-2} xt−2
x t − 1 = a t − 1 × x t − 2 + 1 − a t − 1 × ϵ t − 1 x_{t-1} = \sqrt{a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t-1}} \times ϵ_{t-1} xt−1=at−1×xt−2+1−at−1×ϵt−1
⇓ \Downarrow ⇓
x t = a t ( a t − 1 × x t − 2 + 1 − a t − 1 ϵ t − 1 ) + 1 − a t × ϵ t x_t = \sqrt{a_{t}} (\sqrt{a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t-1}} ϵ_{t-1}) + \sqrt{1-a_t} \times ϵ_t xt=at(at−1×xt−2+1−at−1ϵt−1)+1−at×ϵt
⇓ \Downarrow ⇓
x t = a t a t − 1 × x t − 2 + a t ( 1 − a t − 1 ) ϵ t − 1 + 1 − a t × ϵ t x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{a_{t}(1-a_{t-1})} ϵ_{t-1} + \sqrt{1-a_t} \times ϵ_t xt=atat−1×xt−2+at(1−at−1)ϵt−1+1−at×ϵt
Because $N(\mu_{1},\sigma_{1}^{2}) + N(\mu_{2},\sigma_{2}^{2}) = N(\mu_{1}+\mu_{2},\sigma_{1}^{2} + \sigma_{2}^{2})$Proof
x t = a t a t − 1 × x t − 2 + a t ( 1 − a t − 1 ) + 1 − a t × ϵ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{a_{t}(1-a_{t-1}) + 1-a_t} \times ϵ xt=atat−1×xt−2+at(1−at−1)+1−at×ϵ
⇓ \Downarrow ⇓
x t = a t a t − 1 × x t − 2 + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t}a_{t-1}} \times ϵ xt=atat−1×xt−2+1−atat−1×ϵ
2.2 Relationship between x t x_t xt and x t − 3 x_{t-3} xt−3
x t − 2 = a t − 2 × x t − 3 + 1 − a t − 2 × ϵ t − 2 x_{t-2} = \sqrt{a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t-2}} \times ϵ_{t-2} xt−2=at−2×xt−3+1−at−2×ϵt−2
⇓ \Downarrow ⇓
x t = a t a t − 1 ( a t − 2 × x t − 3 + 1 − a t − 2 ϵ t − 2 ) + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}}(\sqrt{a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t-2}} ϵ_{t-2}) + \sqrt{1-a_{t}a_{t-1}}\times ϵ xt=atat−1(at−2×xt−3+1−at−2ϵt−2)+1−atat−1×ϵ
⇓ \Downarrow ⇓
x t = a t a t − 1 a t − 2 × x t − 3 + a t a t − 1 ( 1 − a t − 2 ) ϵ t − 2 + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{a_{t}a_{t-1}(1-a_{t-2})} ϵ_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times ϵ xt=atat−1at−2×xt−3+atat−1(1−at−2)ϵt−2+1−atat−1×ϵ
⇓ \Downarrow ⇓
x t = a t a t − 1 a t − 2 × x t − 3 + a t a t − 1 − a t a t − 1 a t − 2 ϵ t − 2 + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{a_{t}a_{t-1}-a_{t}a_{t-1}a_{t-2}} ϵ_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times ϵ xt=atat−1at−2×xt−3+atat−1−atat−1at−2ϵt−2+1−atat−1×ϵ
⇓ \Downarrow ⇓
x t = a t a t − 1 a t − 2 × x t − 3 + ( a t a t − 1 − a t a t − 1 a t − 2 ) + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{(a_{t}a_{t-1}-a_{t}a_{t-1}a_{t-2}) + 1-a_{t}a_{t-1}} \times ϵ xt=atat−1at−2×xt−3+(atat−1−atat−1at−2)+1−atat−1×ϵ
⇓ \Downarrow ⇓
x t = a t a t − 1 a t − 2 × x t − 3 + 1 − a t a t − 1 a t − 2 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t}a_{t-1}a_{t-2}} \times ϵ xt=atat−1at−2×xt−3+1−atat−1at−2×ϵ
2.3 Relationship between x t x_t xt and x 0 x_0 x0
- x t = a t a t − 1 × x t − 2 + 1 − a t a t − 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times ϵ xt=atat−1×xt−2+1−atat−1×ϵ
- x t = a t a t − 1 a t − 2 × x t − 3 + 1 − a t a t − 1 a t − 2 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t}a_{t-1}a_{t-2}}\times ϵ xt=atat−1at−2×xt−3+1−atat−1at−2×ϵ
- x t = a t a t − 1 a t − 2 a t − 3 . . . a t − ( k − 2 ) a t − ( k − 1 ) × x t − k + 1 − a t a t − 1 a t − 2 a t − 3 . . . a t − ( k − 2 ) a t − ( k − 1 ) × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times x_{t-k} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times ϵ xt=atat−1at−2at−3...at−(k−2)at−(k−1)×xt−k+1−atat−1at−2at−3...at−(k−2)at−(k−1)×ϵ
- x t = a t a t − 1 a t − 2 a t − 3 . . . a 2 a 1 × x 0 + 1 − a t a t − 1 a t − 2 a t − 3 . . . a 2 a 1 × ϵ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times x_{0} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times ϵ xt=atat−1at−2at−3...a2a1×x0+1−atat−1at−2at−3...a2a1×ϵ
a ˉ t : = a t a t − 1 a t − 2 a t − 3 . . . a 2 a 1 \bar{a}_{t} := a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1} aˉt:=atat−1at−2at−3...a2a1
x t = a ˉ t × x 0 + 1 − a ˉ t × ϵ , ϵ ∼ N ( 0 , I ) x_{t} = \sqrt{\bar{a}_t}\times x_0+ \sqrt{1-\bar{a}_t}\times ϵ , ϵ \sim N(0,I) xt=aˉt×x0+1−aˉt×ϵ,ϵ∼N(0,I)
⇓ \Downarrow ⇓
q ( x t ∣ x 0 ) = 1 2 π 1 − a ˉ t e ( − 1 2 ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } q(xt∣x0)=2π1−aˉt1e(−211−aˉt(xt−aˉtx0)2)
3.Reverse Process p p p
Because P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{ P(B|A)P(A) }{ P(B) } P(A∣B)=P(B)P(B∣A)P(A)
p ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) × q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) p(x_{t-1}|x_{t},x_{0}) = \frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} p(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)×q(xt−1∣x0)
| $$x_{t} = \sqrt{a_t}x_{t-1}+\sqrt{1-a_t}\times ϵ$$ | ~ | $N(\sqrt{a_t}x_{t-1}, 1-a_{t})$ |
| $$x_{t-1} = \sqrt{\bar{a}_{t-1}}x_0+ \sqrt{1-\bar{a}_{t-1}}\times ϵ$$ | ~ | $N( \sqrt{\bar{a}_{t-1}}x_0, 1-\bar{a}_{t-1})$ |
| $$x_{t} = \sqrt{\bar{a}_{t}}x_0+ \sqrt{1-\bar{a}_{t}}\times ϵ$$ | ~ | $N( \sqrt{\bar{a}_{t}}x_0, 1-\bar{a}_{t})$ |
q ( x t ∣ x t − 1 , x 0 ) = 1 2 π 1 − a t e ( − 1 2 ( x t − a t x t − 1 ) 2 1 − a t ) q(x_{t}|x_{t-1},x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) } q(xt∣xt−1,x0)=2π1−at1e(−211−at(xt−atxt−1)2)
q ( x t − 1 ∣ x 0 ) = 1 2 π 1 − a ˉ t − 1 e ( − 1 2 ( x t − 1 − a ˉ t − 1 x 0 ) 2 1 − a ˉ t − 1 ) q(x_{t-1}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} \right ) } q(xt−1∣x0)=2π1−aˉt−11e(−211−aˉt−1(xt−1−aˉt−1x0)2)
q ( x t ∣ x 0 ) = 1 2 π 1 − a ˉ t e ( − 1 2 ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } q(xt∣x0)=2π1−aˉt1e(−211−aˉt(xt−aˉtx0)2)
q ( x t ∣ x t − 1 , x 0 ) × q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = [ 1 2 π 1 − a t e ( − 1 2 ( x t − a t x t − 1 ) 2 1 − a t ) ] ∗ [ 1 2 π 1 − a ˉ t − 1 e ( − 1 2 ( x t − 1 − a ˉ t − 1 x 0 ) 2 1 − a ˉ t − 1 ) ] ÷ [ 1 2 π 1 − a ˉ t e ( − 1 2 ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) ] \frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} = \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) } \right ] * \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} \right ) } \right ] \div \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } \right ] q(xt∣x0)q(xt∣xt−1,x0)×q(xt−1∣x0)=[2π1−at1e(−211−at(xt−atxt−1)2)]∗[2π1−aˉt−11e(−211−aˉt−1(xt−1−aˉt−1x0)2)]÷[2π1−aˉt1e(−211−aˉt(xt−aˉtx0)2)]
⇓ \Downarrow ⇓
2 π 1 − a ˉ t 2 π 1 − a t 2 π 1 − a ˉ t − 1 e [ − 1 2 ( ( x t − a t x t − 1 ) 2 1 − a t + ( x t − 1 − a ˉ t − 1 x 0 ) 2 1 − a ˉ t − 1 − ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) ] \frac{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}}{\sqrt{2\pi} \sqrt{1-a_{t}} \sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}} } e^{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) \right ] } 2π1−at2π1−aˉt−12π1−aˉte[−21(1−at(xt−atxt−1)2+1−aˉt−1(xt−1−aˉt−1x0)2−1−aˉt(xt−aˉtx0)2)]
⇓ \Downarrow ⇓
1 2 π ( 1 − a t 1 − a ˉ t − 1 1 − a ˉ t ) e x p [ − 1 2 ( ( x t − a t x t − 1 ) 2 1 − a t + ( x t − 1 − a ˉ t − 1 x 0 ) 2 1 − a ˉ t − 1 − ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) ] \frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}} \right ) } exp{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_t} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) \right ] } 2π(1−aˉt1−at1−aˉt−1)1exp[−21(1−at(xt−atxt−1)2+1−aˉt−1(xt−1−aˉt−1x0)2−1−aˉt(xt−aˉtx0)2)]
⇓ \Downarrow ⇓
1 2 π ( 1 − a t 1 − a ˉ t − 1 1 − a ˉ t ) e x p [ − 1 2 ( x t 2 − 2 a t x t x t − 1 + a t x t − 1 2 1 − a t + x t − 1 2 − 2 a ˉ t − 1 x 0 x t − 1 + a ˉ t − 1 x 0 2 1 − a ˉ t − 1 − ( x t − a ˉ t x 0 ) 2 1 − a ˉ t ) ] \frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}} \right ) } exp \left[ -\frac{1}{2} \left ( \frac{ x_{t}^2-2\sqrt{a_t}x_{t}x_{t-1}+{a_t}x_{t-1}^2 }{1-a_t} + \frac{ x_{t-1}^2-2\sqrt{\bar{a}_{t-1}}x_0x_{t-1}+\bar{a}_{t-1}x_0^2 }{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right) \right] 2π(1−aˉt1−at1−aˉt−1)1exp[−21(1−atxt2−2atxtxt−1+atxt−12+1−aˉt−1xt−12−2aˉt−1x0xt−1+aˉt−1x02−1−aˉt(xt−aˉtx0)2)]
⇓ \Downarrow ⇓
1 2 π ( 1 − a t 1 − a ˉ t − 1 1 − a ˉ t ) e x p [ − 1 2 ( x t − 1 − ( a t ( 1 − a ˉ t − 1 ) 1 − a ˉ t x t + a ˉ t − 1 ( 1 − a t ) 1 − a ˉ t x 0 ) ) 2 ( 1 − a t 1 − a ˉ t − 1 1 − a ˉ t ) 2 ] \frac{1}{\sqrt{2\pi} \left ( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right ) } exp \left[ -\frac{1}{2} \frac{ \left( x_{t-1} - \left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0} \right) \right) ^2 } { \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right)^2 } \right] 2π(1−aˉt1−at1−aˉt−1)1exp −21(1−aˉt1−at1−aˉt−1)2(xt−1−(1−aˉtat(1−aˉt−1)xt+1−aˉtaˉt−1(1−at)x0))2
⇓ \Downarrow ⇓
p ( x t − 1 ∣ x t ) ∼ N ( a t ( 1 − a ˉ t − 1 ) 1 − a ˉ t x t + a ˉ t − 1 ( 1 − a t ) 1 − a ˉ t x 0 , ( 1 − a t 1 − a ˉ t − 1 1 − a ˉ t ) 2 ) p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0} , \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right)^2 \right) p(xt−1∣xt)∼N(1−aˉtat(1−aˉt−1)xt+1−aˉtaˉt−1(1−at)x0,(1−aˉt1−at1−aˉt−1)2)
Because x t = a ˉ t × x 0 + 1 − a ˉ t × ϵ x_{t} = \sqrt{\bar{a}_t}\times x_0+ \sqrt{1-\bar{a}_t}\times ϵ xt=aˉt×x0+1−aˉt×ϵ, x 0 = x t − 1 − a ˉ t × ϵ a ˉ t x_0 = \frac{x_t - \sqrt{1-\bar{a}_t}\times ϵ}{\sqrt{\bar{a}_t}} x0=aˉtxt−1−aˉt×ϵ. Substitute x 0 x_0 x0 with this formula.
p ( x t − 1 ∣ x t ) ∼ N ( a t ( 1 − a ˉ t − 1 ) 1 − a ˉ t x t + a ˉ t − 1 ( 1 − a t ) 1 − a ˉ t × x t − 1 − a ˉ t × ϵ a ˉ t , β t ( 1 − a ˉ t − 1 ) 1 − a ˉ t ) p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}\times \frac{x_t - \sqrt{1-\bar{a}_t}\times ϵ}{\sqrt{\bar{a}_t}} } , {\color{Red} \frac{ \beta_{t} (1-\bar{a}_{t-1}) } { 1-\bar{a}_{t}}} \right) p(xt−1∣xt)∼N(1−aˉtat(1−aˉt−1)xt+1−aˉtaˉt−1(1−at)×aˉtxt−1−aˉt×ϵ,1−aˉtβt(1−aˉt−1))