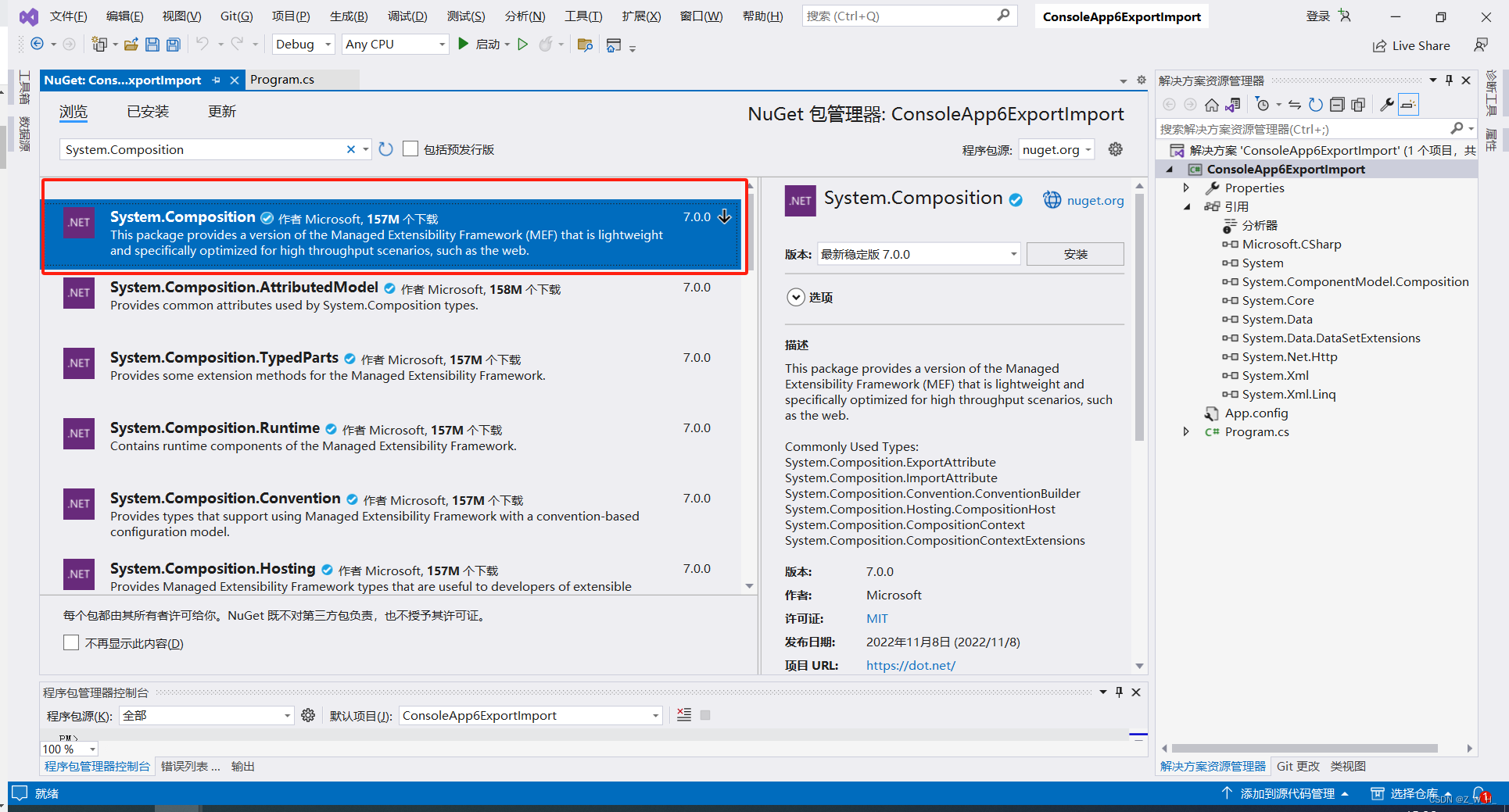
0. 内容

1. VIO回顾

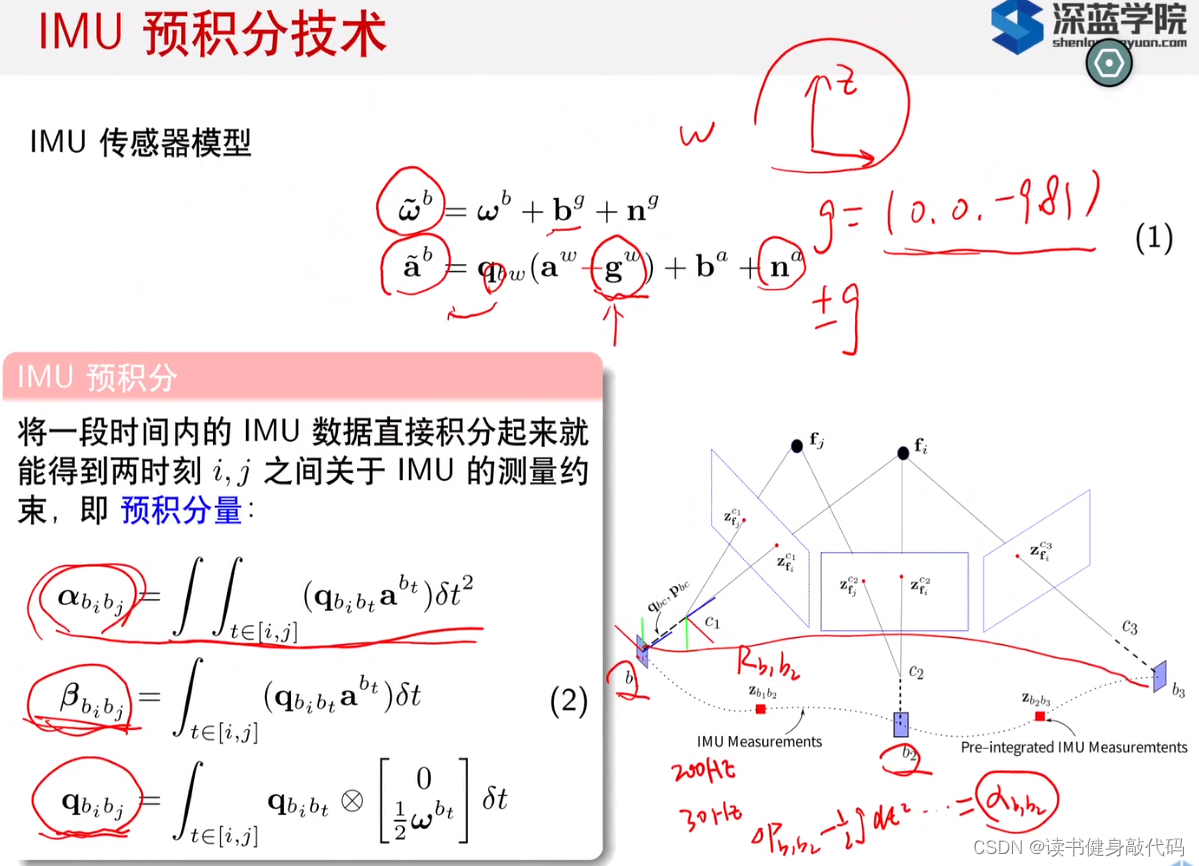
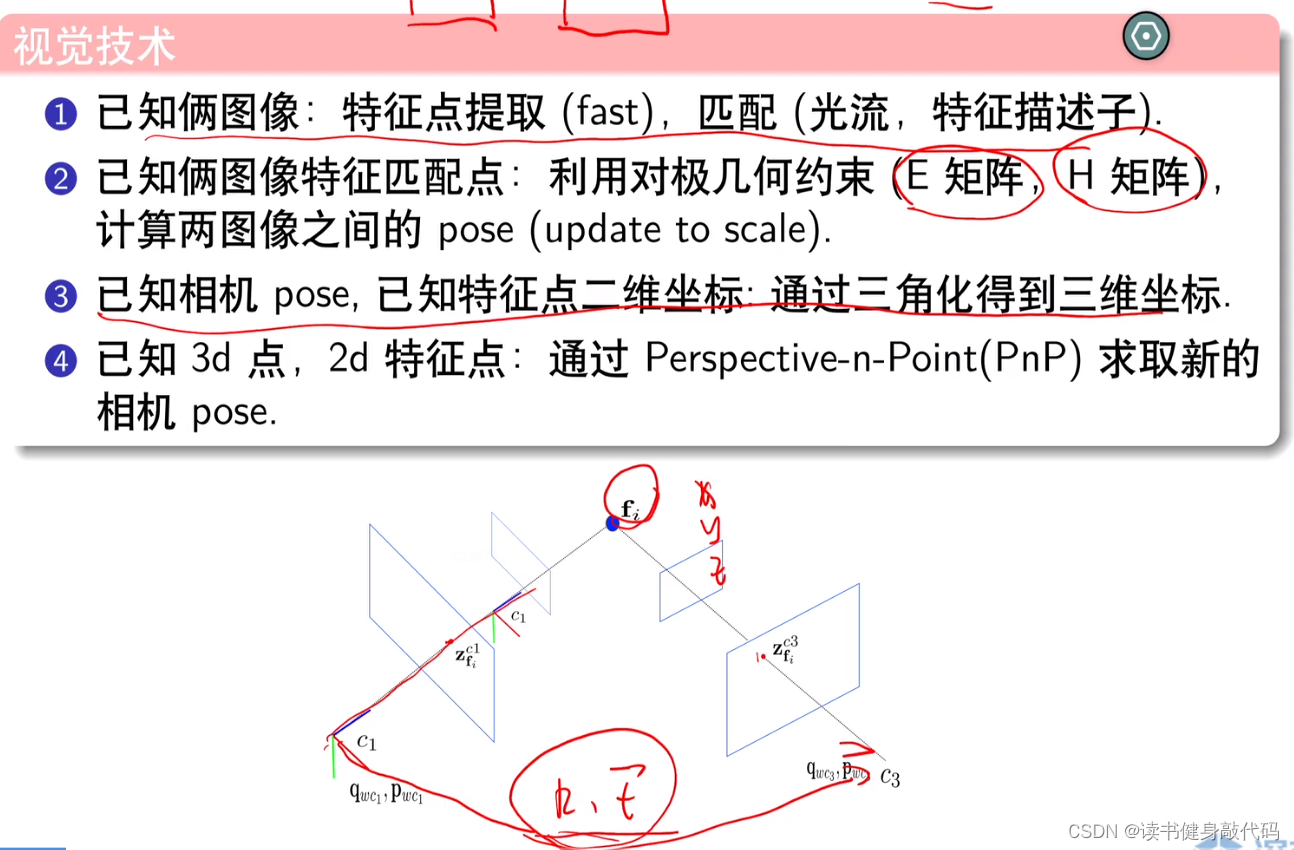
整个视觉前端pipeline回顾：

1. 两帧图像，可提取特征点，特征匹配（描述子暴力匹配或者光流）
2. 已知特征点匹配关系，利用几何约束计算relative pose([R|t])，translation只有方向，没有尺度
3. 使用三角化获得3维坐标，即可完成vslam系统的初始化
4. 有了3D特征点，后续可根据特征跟踪，使用PnP求解Camera Pose，无需再使用几何约束

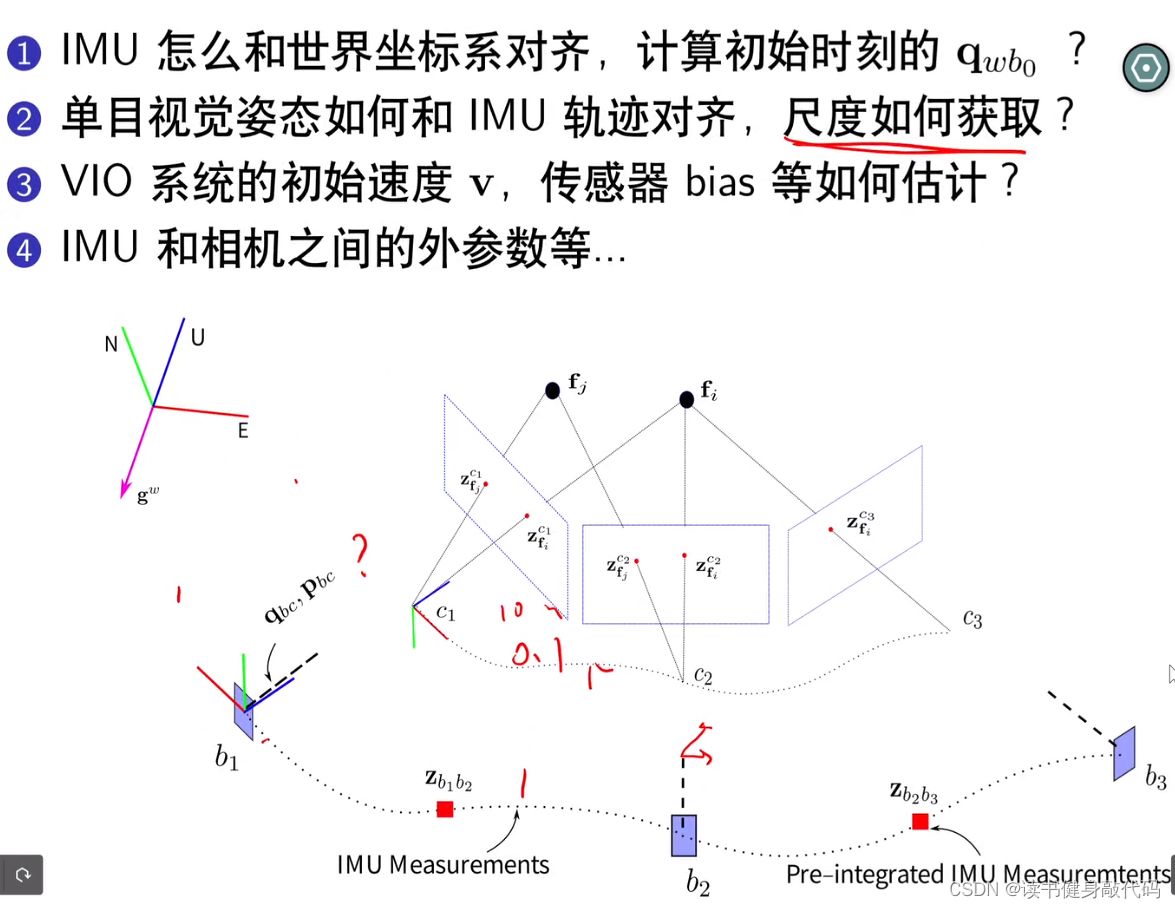
1. IMU的加速度要和世界系的重力进行对齐
   
   世界系重力假设(0，0，-9.81)，IMU第一帧估计出一个${}^{c}g{=}^c{R}_{cb}{g}_b$，就可以求出第一帧camera在world下的pose（带头大哥）

2. 视觉的尺度和IMU尺度要进行对齐

3. VIO系统速度，传感器bias需要估计

4. IMU和相机的外参Tic

知道了z轴的法向量就能估计roll和pitch(tilt)，但是yaw不可观。

2. VINS鲁棒初始化

2.1 pipeline overview

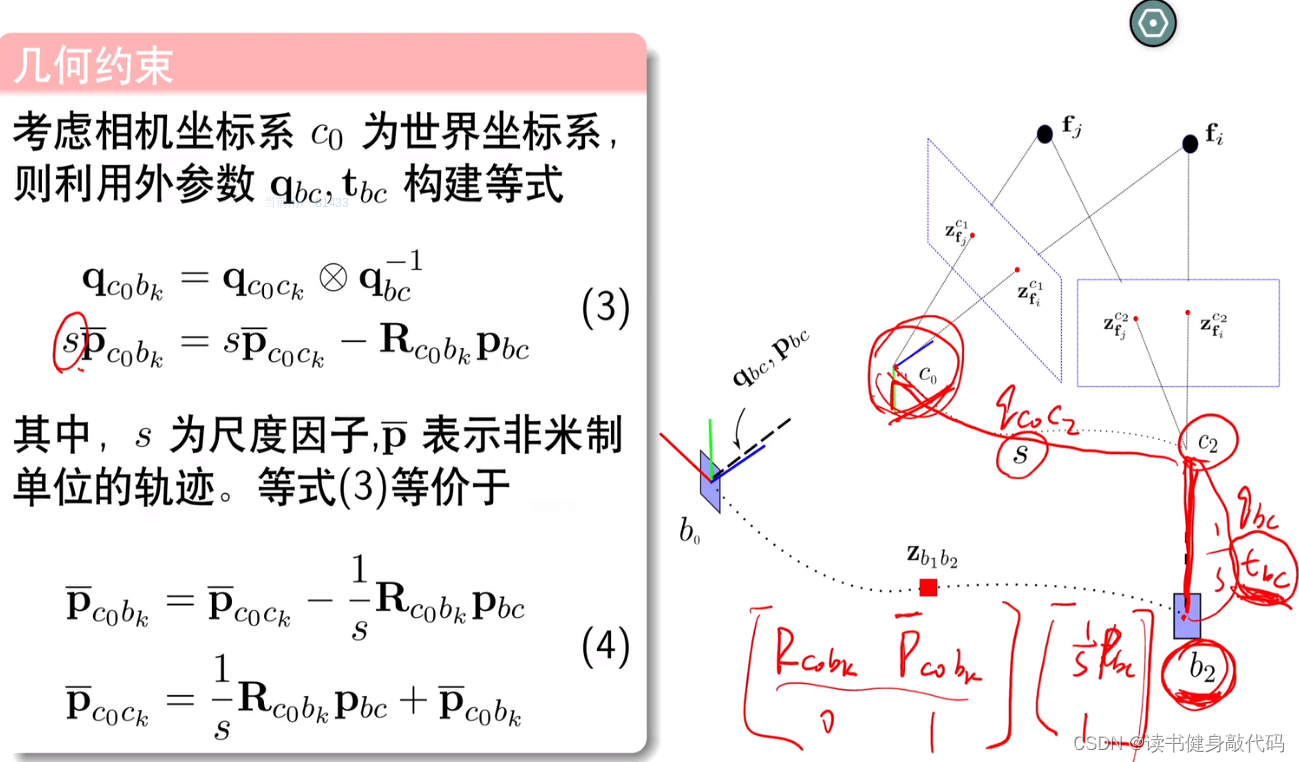
IMU积分是米制单位，但是camera不是，camera存在一个缩放因子，标定出外参$[R_{bc},t_{bc}]$之后，可以求得尺度因子s，先对坐标系，R,t的数学表示做一下说明：
旋转脚标相连时相消，刚性连接在不同时刻的的观测相同，平移左上角是观测系，右下角从左到右；平移乘旋转后平移向量不变，但观测系改变。

式(4)第一行这样理解：
$${}^{c_0}{\overline{p}}_{c_0{b}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}-\frac{1}{s}{}^{c_0}{R}_{c_0{b}_k}{}^b{p}_{bc}(2.1)$$
左上角都是观测系，即在什么系下看这个量，由于刚性连接在不同观测系，不同时间下相同，且平移乘旋转后旋转向量不变，但观测系改变，所以$${}^b{p}_{bc}={}^{b_k}{p}_{b_k{c}_k}(2.2)$$
所以将(2.2)带入式(2.1)可得：
$${}^{c_0}{\overline{p}}_{c_0{b}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}-{}^{c_0}{\overline{p}}_{b_k{c}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}+{}^{c_0}{\overline{p}}_{c_k{b}_k}(2.3)$$
即在$c_0$系下进行将${}^{c_0}{\overline{p}}_{c_0{c}_k}+{}^{c_0}{\overline{p}}_{c_k{b}_k}$向量相加，不难理解。
标定出Camera和IMU外参之后，利用式(2.1)就可以求出尺度因子。

Tbc外参的Rotation很重要，而Translation由于可能离得比较近，所以相对来说没有Rotation重要

2.2 外参估计

旋转约束：两种路径求取的$q_{c_k{b}_{k+1}}$应该相同。

这里的未知量只有外参$q_{bc}$，也可以简单地理解为一段时间内，camera出一段pose(trajectory)，imu积分出一段pose(trajectory)，这两段pose理想情况下只有外参的差异，（不考虑$t_{bc}$的情况下）可以将这两段pose align起来，残差是两段pose align的残差，待估计量就是外参，做LSP的结果就是外参。

VINS论文中将多个时刻的数据累计起来，并使用了鲁棒核函数对每一项进行了加权，权值计算方法：有$tr(R)=1+2cos\theta$（可以看wiki），式(9)中的那一大块矩阵就是式（5）移项而得，因为求的是相同的量（如$q_{c_k{b}_{k+1}}$），所以理想情况下连乘应该是Identity，但实际上，如果外参估的不准，这个角度会较大（>threshole），所以式（8）将大于threshold的部分的权值设的较小，进行了抑制。

最终对$q_{bc}$的求解还是对式(7)使用SVD分解，取$V^T$最后一列作为解。

(参考这篇博客参考这篇博客中使用Lanrange算子证明取$V^T$最后一列是我们所求的解。)

论文中还对SVD分解的倒数第二小奇异值进行了判断，如果小于阈值则认为该次估计无效，重新采集数据进行估计。（这和增多数据来提升数据信噪比是一样的目的，都是为了提高数值稳定性）

2.3 gyro bias估计

式(10)就是将$b_k$到$b_{k+1}$时刻之间imu的rotation都转到$c_0$系下进行align：

• 前两项四元数相乘代表求在$c_0$系下看imu在$b_k$到$b_{k+1}$时刻之间的relative rotation
• 第3项$q_{b_k{b}_{k+1}}$是IMU积分而来的两时刻间的relative rotation真值（会受到gyro bias的影响），对其进行一阶Taylor展开，带入(10)，(10)即代表一阶项所代表的${\theta }_{err}$，可以求出gyro bias

这跟前面估计外参的是一样的，都是使用的旋转约束。

2.4 初始化速度，重力，尺度因子