文章目录
- 极限(上)超链接
- 5、极限存在法则
- 5.1、夹逼准则
- 5.1.1、数列夹逼准则
- 5.1.2、函数夹逼准则
- 5.1.3、第一重要极限
- 5.2、单调有界准则
- 5.2.1、第二重要极限
- 6、函数的连续性与间断点
- 6.1、函数的连续性
- 6.1.1、定义
- 6.1.2、左连续右连续
- 6.2、函数的间断点
- 6.2.1、第一类间断点
- 6.2.2、第二类间断点
- 7、连续函数的运算与初等函数的连续性
- 7.1、连续函数和、差、积、商的连续性
- 7.2、反函数的连续性
- 7.3、复合函数的连续性
- 7.4、初等函数的连续性
- 8、闭区间上连续函数的性质
- 8.1、有界性与最大最小值定理
- 8.2、零点定理与介值定理
极限(上)超链接
【高等数学】极限(上)
5、极限存在法则
5.1、夹逼准则
5.1.1、数列夹逼准则
准则:如果数列{
x
n
x_n
xn},{
y
n
y_n
yn}及{
z
n
z_n
zn}满足以下条件:
(1) 存在
N
N
N,当
n
>
N
n >N
n>N时,
x
n
≤
y
n
≤
z
n
x_n\leq y_n\leq z_n
xn≤yn≤zn
(2)
lim
n
→
∞
x
n
=
lim
n
→
∞
z
n
=
a
\lim_{n \to ∞}x_n=\lim_{n \to ∞}z_n=a
limn→∞xn=limn→∞zn=a
则:
lim
n
→
∞
y
n
=
a
\lim_{n \to ∞}y_n=a
limn→∞yn=a
【证明】
∵
lim
n
→
∞
x
n
=
lim
n
→
∞
z
n
=
a
∵\lim_{n \to ∞}x_n=\lim_{n \to ∞}z_n=a
∵limn→∞xn=limn→∞zn=a
∀
ϵ
>
0
,
∃
N
,
当
n
>
N
时
,
∣
x
n
−
a
∣
<
ϵ
且
∣
z
n
−
a
∣
<
ϵ
\forall\epsilon>0,\exist N,当n>N时,|x_n-a|<\epsilon且|z_n-a|<\epsilon
∀ϵ>0,∃N,当n>N时,∣xn−a∣<ϵ且∣zn−a∣<ϵ
⇛
a
−
ϵ
<
x
n
<
a
+
ϵ
\Rrightarrow a-\epsilon<x_n<a+\epsilon
⇛a−ϵ<xn<a+ϵ
a
−
ϵ
<
z
n
<
a
+
ϵ
a-\epsilon<z_n<a+\epsilon
a−ϵ<zn<a+ϵ
由
n
>
N
n>N
n>N时,
x
n
≤
y
n
≤
z
n
x_n\leq y_n\leq z_n
xn≤yn≤zn得
⇛
a
−
ϵ
<
x
n
≤
y
n
≤
z
n
<
a
+
ϵ
\Rrightarrow a-\epsilon<x_n\leq y_n\leq z_n<a+\epsilon
⇛a−ϵ<xn≤yn≤zn<a+ϵ
即:
∣
y
n
−
a
∣
<
ϵ
|y_n-a|<\epsilon
∣yn−a∣<ϵ
证毕
5.1.2、函数夹逼准则
准则:如果
(1)、当
x
∈
U
˚
(
x
0
,
δ
)
x \in\mathring U(x_0,\delta)
x∈U˚(x0,δ)时,
f
(
x
)
≤
g
(
x
)
≤
h
(
x
)
f(x)\leq g(x)\leq h(x)
f(x)≤g(x)≤h(x)
(2)、
lim
x
→
x
0
g
(
x
)
=
a
\lim_{x \to x_0}g(x)=a
limx→x0g(x)=a
则
lim
x
→
x
0
g
(
x
)
=
a
\lim_{x \to x_0}g(x)=a
limx→x0g(x)=a
证明与数列极限完全一致
5.1.3、第一重要极限
lim x → 0 sin x x = 1 \lim_{x \to 0}\frac{\sin x}{x}=1 limx→0xsinx=1
【证明】
如图:

以圆心O做一个半径为1的单位圆
其中:
∠
B
O
A
=
x
∠BOA=x
∠BOA=x,
B
D
⊥
O
A
BD⊥OA
BD⊥OA,
O
B
=
O
A
=
1
OB=OA=1
OB=OA=1
由图我们可得:
S
▲
O
B
A
<
S
扇形
O
B
A
<
S
▲
O
C
A
S_{▲OBA}<S_{扇形OBA}<S_{▲OCA}
S▲OBA<S扇形OBA<S▲OCA
S
▲
O
B
A
=
1
2
B
D
×
O
B
∵
sin
x
=
B
D
O
B
=
B
D
∴
S
▲
O
B
A
=
1
2
sin
x
S_{▲OBA}=\frac{1}{2}BD\times OB∵\sin x=\frac{BD}{OB}=BD∴S_{▲OBA}=\frac{1}{2}\sin x
S▲OBA=21BD×OB∵sinx=OBBD=BD∴S▲OBA=21sinx
S
扇形
O
B
A
=
x
π
2
π
=
1
2
x
S_{扇形OBA}=\frac{x\pi}{2\pi}=\frac{1}{2}x
S扇形OBA=2πxπ=21x
S
▲
O
C
A
=
1
2
A
C
×
O
A
∵
tan
x
=
A
C
O
A
=
A
C
∴
S
▲
O
C
A
=
1
2
tan
x
S_{▲OCA}=\frac{1}{2}AC\times OA∵\tan x=\frac{AC}{OA}=AC∴S_{▲OCA}=\frac{1}{2}\tan x
S▲OCA=21AC×OA∵tanx=OAAC=AC∴S▲OCA=21tanx
∴
sin
x
<
x
<
tan
x
(
x
∈
[
0
,
π
2
)
\sin x < x<\tan x(x\in[0,\frac{\pi}{2})
sinx<x<tanx(x∈[0,2π)
1
<
x
sin
x
<
1
cos
x
⇛
cos
x
<
sin
x
x
<
1
⇛
0
<
1
−
sin
x
x
<
1
−
cos
x
1<\frac{x}{\sin x}<\frac{1}{\cos x}\Rrightarrow \cos x<\frac{\sin x}{x}<1\Rrightarrow0<1-\frac{\sin x}{x}<1-\cos x
1<sinxx<cosx1⇛cosx<xsinx<1⇛0<1−xsinx<1−cosx
1
−
cos
x
=
2
s
i
n
2
x
2
≤
2
(
x
2
)
2
→
0
1-\cos x =2sin^2\frac{x}{2}\leq2(\frac{x}{2})^2\to0
1−cosx=2sin22x≤2(2x)2→0
∴
sin
x
x
=
1
∴\frac{\sin x}{x}= 1
∴xsinx=1
证毕
而有了这个极限我们就可以证明以下的这些常用的极限:
(1)
lim
x
→
0
tan
x
x
=
1
\lim_{x \to 0}\frac{\tan x}{x}= 1
limx→0xtanx=1
(2)
lim
x
→
0
1
−
cos
x
x
2
=
1
2
\lim_{x \to 0}\frac{1-\cos x}{x^2}=\frac{1}{2}
limx→0x21−cosx=21
(3)
lim
x
→
0
arctan
x
x
=
1
\lim_{x \to 0}\frac{\arctan x}{x}=1
limx→0xarctanx=1
【证明】
(1)
tan
x
x
=
sin
x
x
cos
x
=
1
×
1
cos
x
=
1
\frac{\tan x}{x}=\frac{\sin x}{x\cos x}=1\times\frac{1}{\cos x}=1
xtanx=xcosxsinx=1×cosx1=1(证
sin
x
x
\frac{\sin x}{x}
xsinx时证明过
lim
x
→
0
cos
x
=
1
\lim_{x \to 0}\cos x = 1
limx→0cosx=1)
(2) 1 − cos x x 2 = 2 sin 2 x 2 x 2 = 1 2 \frac{1-\cos x}{x^2}=\frac{2\sin^2 \frac{x}{2}}{x^2}=\frac{1}{2} x21−cosx=x22sin22x=21
(3)
令
arctan
x
=
t
,
x
=
tan
t
令\arctan x=t,x=\tan t
令arctanx=t,x=tant
原式
=
t
tan
t
=
1
=\frac{t}{\tan t}=1
=tantt=1
5.2、单调有界准则
(1)、准则:单调有界数列必有极限
即:单调增上有界,单调减下有界的数列必有极限
我们从几何上来看是非常明显的,如果一个数列是单调增的那么它一定下有界,此时只要它上有界那么就一定有极限,反过来单减也是一个道理
5.2.1、第二重要极限
lim
n
→
∞
(
1
+
1
n
)
n
=
e
\lim_{n \to ∞}(1+\frac{1}{n})^n=e
n→∞lim(1+n1)n=e
【证明第二重要极限的存在性】
①首先我们需要证明这个极限是单增/单减的
把
n
=
1
,
n
=
2
n=1,n=2
n=1,n=2分别带入初步判断为单增
现在就要证明
lim
n
→
∞
(
1
+
1
n
)
n
≤
lim
n
→
∞
(
1
+
1
n
+
1
)
n
+
1
\lim_{n \to ∞}(1+\frac{1}{n})^n\leq\lim_{n \to ∞}(1+\frac{1}{n+1})^{n+1}
limn→∞(1+n1)n≤limn→∞(1+n+11)n+1
其中,左边我们可以看成n个
(
1
+
1
n
)
(1+\frac{1}{n})
(1+n1)相乘
根据均值不等式
即:
a
1
+
a
2
+
a
3
+
.
.
.
+
a
n
n
≥
n
a
1
a
2
a
3
.
.
.
a
n
\frac{a_1+a_2+a_3+...+a_n}{n}\geq^n\sqrt{a_1a_2a_3...a_n}
na1+a2+a3+...+an≥na1a2a3...an
得:
(
1
+
1
n
)
n
≤
(
n
+
1
n
)
n
(1+\frac{1}{n})^n\leq(\frac{n+1}{n})^n
(1+n1)n≤(nn+1)n
此时我们再在左边式子乘1:
(
1
+
1
n
)
n
×
1
≤
(
n
+
1
+
1
n
+
1
)
n
+
1
(1+\frac{1}{n})^n\times 1\leq(\frac{n+1+1}{n+1})^{n+1}
(1+n1)n×1≤(n+1n+1+1)n+1
而
(
1
+
1
n
+
1
)
n
+
1
=
(
n
+
1
+
1
n
+
1
)
n
+
1
(1+\frac{1}{n+1})^{n+1}=(\frac{n+1+1}{n+1})^{n+1}
(1+n+11)n+1=(n+1n+1+1)n+1
∴
(
1
+
1
n
)
n
≤
(
1
+
1
n
+
1
)
n
+
1
∴(1+\frac{1}{n})^n\leq(1+\frac{1}{n+1})^{n+1}
∴(1+n1)n≤(1+n+11)n+1
②然后我们再证明上有界
(
1
+
1
n
)
n
=
(
1
+
1
n
)
(
1
+
1
n
)
(
1
+
1
n
)
.
.
.
(
1
+
1
n
)
×
1
2
×
1
2
≤
(
n
+
1
+
1
n
+
2
)
n
+
2
=
1
(1+\frac{1}{n})^n=(1+\frac{1}{n})(1+\frac{1}{n})(1+\frac{1}{n})...(1+\frac{1}{n})\times \frac{1}{2}\times\frac{1}{2}\leq(\frac{n+1+1}{n+2})^{n+2}=1
(1+n1)n=(1+n1)(1+n1)(1+n1)...(1+n1)×21×21≤(n+2n+1+1)n+2=1
即
(
1
+
1
n
)
n
≤
4
(1+\frac{1}{n})^n\leq 4
(1+n1)n≤4
根据①②证得
lim
n
→
∞
(
1
+
1
n
)
n
\lim_{n \to ∞}(1+\frac{1}{n})^n
limn→∞(1+n1)n极限存在
因为这个极限存在,我们把第二重要极限的极限记为e,后来就得到了我们熟知的无理数e
而第一和第二重要极限不仅仅数列极限适用,而且函数极限也同样适用
证明:
lim
x
→
∞
(
1
+
1
x
)
x
=
e
\lim_{x \to ∞}(1+\frac{1}{x})^x=e
limx→∞(1+x1)x=e
证明这个函数我们需要用到取整函数,并用到以下结论
x
−
1
≤
[
x
]
≤
x
x-1\leq[x]\leq x
x−1≤[x]≤x
思路:通过这个不等式,我们把这个函数进行缩小和放大再适用夹逼准则即可证明
(
1
+
1
[
x
]
+
1
)
[
x
]
−
1
=
e
[
x
]
−
1
[
x
]
+
1
=
e
≤
(
1
+
1
x
)
x
≤
(
1
+
1
[
x
]
)
[
x
+
1
]
=
(
1
+
1
[
x
]
)
[
x
]
(
1
+
1
[
x
]
)
=
e
(1+\frac{1}{[x]+1})^{[x]-1}=e^{\frac{[x]-1}{[x]+1}}=e\leq(1+\frac{1}{x})^x\leq(1+\frac{1}{[x]})^{[x+1]}=(1+\frac{1}{[x]})^{[x]}(1+\frac{1}{[x]})=e
(1+[x]+11)[x]−1=e[x]+1[x]−1=e≤(1+x1)x≤(1+[x]1)[x+1]=(1+[x]1)[x](1+[x]1)=e
①即
lim
x
→
+
∞
(
1
+
1
x
)
x
=
e
\lim_{x \to +∞}(1+\frac{1}{x})^x=e
limx→+∞(1+x1)x=e
此时再证明
x
→
−
∞
x \to -∞
x→−∞,
(
1
+
1
x
)
x
=
e
(1+\frac{1}{x})^x=e
(1+x1)x=e
令
t
=
−
x
,
t=-x,
t=−x,得:
lim
t
→
+
∞
(
1
−
1
t
)
−
t
=
(
t
t
−
1
)
t
=
(
1
+
1
t
−
1
)
t
−
1
(
1
+
1
t
−
1
)
=
e
\lim_{t \to +∞}(1-\frac{1}{t})^{-t}=(\frac{t}{t-1})^t=(1+\frac{1}{t-1})^{t-1}(1+\frac{1}{t-1})=e
limt→+∞(1−t1)−t=(t−1t)t=(1+t−11)t−1(1+t−11)=e
②即
lim
x
→
−
∞
(
1
+
1
x
)
x
=
e
\lim_{x \to -∞}(1+\frac{1}{x})^x=e
limx→−∞(1+x1)x=e
此时再通过换元法可以得出以下结论
lim
x
→
0
(
1
+
x
)
1
x
=
e
\lim_{x \to 0}(1+x)^{\frac{1}{x}}=e
x→0lim(1+x)x1=e
6、函数的连续性与间断点
6.1、函数的连续性
6.1.1、定义
给一个
x
0
x_0
x0改变量记为
Δ
x
\Delta x
Δx,当
x
0
=
x
0
+
Δ
x
x_0 = x_0+\Delta x
x0=x0+Δx时,函数值的改变量记为
Δ
y
,
而
Δ
y
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
\Delta y,而\Delta y=f(x_0+\Delta x)-f(x_0)
Δy,而Δy=f(x0+Δx)−f(x0),其中这里的
x
x
x为定值,而
Δ
x
\Delta x
Δx是变化的,如图(
y
=
1
x
y=\frac{1}{x}
y=x1):
而当图上的
Δ
x
→
0
\Delta x \to 0
Δx→0时,
Δ
y
→
0
\Delta y \to 0
Δy→0则说明这个函数是连续的
连续定义:若
lim
Δ
x
→
0
Δ
y
=
0
,
也就是
:
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
0
\lim_{\Delta x \to 0}\Delta y=0,也就是:\lim_{\Delta x \to 0}f(x_0+\Delta x)-f(x_0)=0
Δx→0limΔy=0,也就是:Δx→0limf(x0+Δx)−f(x0)=0
则说明
y
=
f
(
x
0
)
y=f(x_0)
y=f(x0)这一点上是连续的
而如果我们把
x
0
+
Δ
x
x_0+\Delta x
x0+Δx看成一个整体换成
x
x
x表示,上述式子还能写成
lim
x
→
x
0
f
(
x
)
−
f
(
x
0
)
=
0
,
也就是
:
lim
x
→
x
0
f
(
x
)
=
f
(
x
0
)
\lim_{x \to x_0}f(x)-f(x_0)=0,也就是:\lim_{x \to x_0}f(x)=f(x_0)
x→x0limf(x)−f(x0)=0,也就是:x→x0limf(x)=f(x0)
6.1.2、左连续右连续
左连续:
lim
x
→
x
0
−
f
(
x
)
=
f
(
x
0
)
\lim_{x \to x_0^-}f(x)=f(x_0)
limx→x0−f(x)=f(x0)
右连续:
lim
x
→
x
0
+
f
(
x
)
=
f
(
x
0
)
\lim_{x \to x_0^+}f(x)=f(x_0)
limx→x0+f(x)=f(x0)
函数连续和左连续右连续的关系:
连续其实讨论的是
x
0
x_0
x0 左右两边的极限值与这一点的函数值之间的关系
也就是说,连续其实就包含了左连续与右连续,就有以下结论
连续
⇚
⇛
左连续
+
右连续
连续\Lleftarrow\Rrightarrow左连续+右连续
连续⇚⇛左连续+右连续
区间连续概念:
(1)、对于
f
(
x
)
f(x)
f(x)在开区间
(
a
,
b
)
(a,b)
(a,b)连续,仅要求区间内部所有点连续,a和b两个端点不要求
(2)、对于
f
(
x
)
f(x)
f(x)在闭区间
[
a
,
b
]
[a,b]
[a,b]连续,要求区间所有点都连续并左端点右连续,右端点左连续
结论: sin x \sin x sinx在区间 ( − ∞ , + ∞ ) 上连续 (-∞,+∞)上连续 (−∞,+∞)上连续
【证明】
证明
sin
x
\sin x
sinx在区间
(
−
∞
,
+
∞
)
(-∞,+∞)
(−∞,+∞)连续
即证明:
∀
x
0
∈
(
−
∞
,
+
∞
)
,
lim
Δ
x
→
0
Δ
y
=
sin
(
x
0
+
Δ
x
)
−
s
i
n
(
x
0
)
=
0
\forall x_0\in (-∞,+∞),\lim_{\Delta x \to 0}\Delta y =\sin(x_0+\Delta x)-sin(x_0)=0
∀x0∈(−∞,+∞),limΔx→0Δy=sin(x0+Δx)−sin(x0)=0
和差化积:
sin
(
x
0
+
Δ
x
)
−
sin
(
x
0
)
=
2
sin
Δ
x
2
cos
2
x
0
+
Δ
x
2
\sin (x_0+\Delta x)-\sin(x_0)=2\sin\frac{\Delta x}{2}\cos\frac{2x_0+\Delta x}{2}
sin(x0+Δx)−sin(x0)=2sin2Δxcos22x0+Δx
∵
Δ
y
→
0
∼
∣
Δ
y
∣
→
0
∵\Delta y \to 0 \sim|\Delta y|\to0
∵Δy→0∼∣Δy∣→0
∴
∣
Δ
y
∣
=
∣
sin
(
x
0
+
Δ
x
)
−
sin
(
x
0
)
∣
=
2
∣
sin
Δ
x
2
∣
∣
cos
2
x
0
+
Δ
x
2
∣
≤
2
sin
∣
Δ
x
∣
2
∴|\Delta y|=|\sin (x_0+\Delta x)-\sin(x_0)|=2|\sin\frac{\Delta x}{2}||\cos\frac{2x_0+\Delta x}{2}|\leq 2\sin\frac{|\Delta x|}{2}
∴∣Δy∣=∣sin(x0+Δx)−sin(x0)∣=2∣sin2Δx∣∣cos22x0+Δx∣≤2sin2∣Δx∣
∵
x
∈
(
0
,
π
2
)
,
sin
x
<
x
<
tan
x
∵x\in(0,\frac{\pi}{2}),\sin x<x<\tan x
∵x∈(0,2π),sinx<x<tanx
∴
2
sin
∣
Δ
x
∣
2
<
2
∣
Δ
x
∣
2
→
0
∴2\sin\frac{|\Delta x|}{2}<2\frac{|\Delta x|}{2}\to0
∴2sin2∣Δx∣<22∣Δx∣→0
∴
Δ
y
→
0
∴\Delta y \to 0
∴Δy→0
证毕
6.2、函数的间断点
如果一个函数在某点上非连续,那么它就是间断的
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处连续的条件:
1、
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0有定义
2、
lim
x
→
x
0
f
(
x
)
存在
\lim_{x \to x_0}f(x)存在
limx→x0f(x)存在
3、
lim
x
→
x
0
f
(
x
)
=
f
(
x
0
)
\lim_{x \to x_0}f(x)=f(x_0)
limx→x0f(x)=f(x0)
根据一个函数不满足上面三个条件(最少一个),我们可以划分出不同类型的间断点
【间断点】
首先,讨论间断点的要求是:
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0去心邻域有定义,因为如果f(x)在去心邻域无定义的话讨论连续间断也就无意义了例如:
ln
x
\ln x
lnx讨论它在
x
=
−
1
x=-1
x=−1处的间断就无意义
间断点的类型我们根据左右极限是否存在可以分为:
1、第一类间断点:左右极限存在
2、第二类间断点:左右极限不存在
6.2.1、第一类间断点
可去间断点:左右极限存在并且相等,但是函数值不等于极限值的点
可去间断点只会出现两种情况:
1)、这一点的函数值不存在
2)、这一点的函数值不等于极限值
我们拿2举例
例如:
f
(
x
)
=
{
−
x
2
x
≠
0
2
x
=
0
f(x)=\begin{cases} -x^2 & x≠0 \\ 2 & x=0 \end{cases}
f(x)={−x22x=0x=0
跳跃间断点:左右极限存在但不相等
例如: f ( x ) = { 2 x ≥ 0 x x < 0 f(x)=\begin{cases} 2 & x\geq0 \\ x & x<0 \end{cases} f(x)={2xx≥0x<0
6.2.2、第二类间断点
第二类间断点是左右极限不存在的间断点
我们都知道,左右极限不存在的原因有两种,一种是趋近于
∞
∞
∞,另一种是左右极限虽然有界,但不趋近于一个确定的值
而这两种原因,也就决定了第二类间断点分为两类
1、无穷间断点:左右极限至少有一个趋近于
∞
∞
∞
例如: y = 1 x y=\frac{1}{x} y=x1
2、振荡间断点:左右极限至少有一个极限虽然不趋近 ∞ ∞ ∞,但不存在
例如: y = sin 1 x y=\sin\frac{1}{x} y=sinx1
7、连续函数的运算与初等函数的连续性
7.1、连续函数和、差、积、商的连续性
定理:设函数
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x)在
x
0
x_0
x0连续
则
f
(
x
)
±
g
(
x
)
,
f
(
x
)
×
g
(
x
)
,
f
(
x
)
g
(
x
)
(
g
(
x
)
≠
0
)
f(x)\pm g(x),f(x)\times g(x),\frac{f(x)}{g(x)}(g(x)≠0)
f(x)±g(x),f(x)×g(x),g(x)f(x)(g(x)=0)都在
x
0
x_0
x0连续
【证明】
1、证明
f
(
x
)
±
g
(
x
)
f(x)\pm g(x)
f(x)±g(x)在
x
0
x_0
x0连续,即证明:
lim
x
→
x
0
f
(
x
)
+
g
(
x
)
=
f
(
x
0
)
+
g
(
x
0
)
\lim_{x \to x_0}f(x)+g(x)=f(x_0)+g(x_0)
limx→x0f(x)+g(x)=f(x0)+g(x0)
lim
x
→
x
0
f
(
x
)
±
g
(
x
)
=
lim
x
→
x
0
f
(
x
)
±
lim
x
→
x
0
g
(
x
)
\lim_{x \to x_0}f(x)\pm g(x)=\lim_{x \to x_0}f(x)\pm\lim_{x \to x_0}g(x)
limx→x0f(x)±g(x)=limx→x0f(x)±limx→x0g(x)
=
f
(
x
0
)
+
g
(
x
0
)
=f(x_0)+g(x_0)
=f(x0)+g(x0)
证毕
而其他的根据极限的四则运算同样的方法既能证明
而此时我们有了这个结论后,就可以尝试证明以下的函数的连续
证明: tan x , cot x \tan x,\cot x tanx,cotx在其定义域内是连续的
首先:我们前面证明了
sin
x
\sin x
sinx在其定义域内是连续的
cos
x
=
sin
(
π
2
−
x
)
\cos x=\sin (\frac{\pi}{2}-x)
cosx=sin(2π−x)所以
cos
x
\cos x
cosx在其定义域内连续
tan
x
=
sin
x
cos
x
\tan x = \frac{\sin x}{\cos x}
tanx=cosxsinx根据连续商的法则得
tan
x
\tan x
tanx在定义域内连续
cot
x
=
cos
x
sin
x
\cot x = \frac{\cos x}{\sin x}
cotx=sinxcosx根据连续商的法则得
cot
x
\cot x
cotx在其定义域内连续
7.2、反函数的连续性
定理:设 f : [ a , b ] → R f:[a,b]\to R f:[a,b]→R是严格单调增(减)的连续函数.则其反函数在 [ f ( a ) , f ( b ) ] / ( [ f ( b ) , f ( a ) ] ) , [f(a),f(b)]/([f(b),f(a)]), [f(a),f(b)]/([f(b),f(a)]),上也是连续的
如图 ( y = e x ) : (y=e^x): (y=ex):

如图
y
=
e
x
y=e^x
y=ex在
[
a
,
b
)
]
[a,b)]
[a,b)]是连续的
即它的反函数
x
=
f
−
(
y
)
=
ln
y
x=f^-(y)=\ln y
x=f−(y)=lny在
[
f
(
a
)
,
f
(
b
)
]
[f(a),f(b)]
[f(a),f(b)]上也是连续的
根据这个定理,我们可以得出以下初等函数在其定义域内都是连续的
arcsin
x
,
arccos
x
,
arctan
x
,
a
r
c
c
o
t
\arcsin x,\arccos x,\arctan x,arccot
arcsinx,arccosx,arctanx,arccot
x
x
x
7.3、复合函数的连续性
定理:设
y
=
f
(
g
(
x
)
)
y =f(g(x))
y=f(g(x))是由
y
=
f
(
u
)
y = f(u)
y=f(u)与
u
=
g
(
x
)
u =g(x)
u=g(x)复合而成,若
g
(
x
)
g(x)
g(x)在
x
0
x_0
x0处连续,
f
(
u
)
f(u)
f(u)在
u
0
u_0
u0连续,
u
0
=
g
(
x
0
)
,
u_0=g(x_0),
u0=g(x0),则
f
(
g
(
x
)
)
f(g(x))
f(g(x))在
x
0
x_0
x0处连续
即:
lim
x
→
x
0
g
(
x
)
=
g
(
x
0
)
且
lim
u
→
u
0
f
(
u
)
=
f
(
u
0
)
且
u
0
=
g
(
x
0
)
\lim_{x \to x_0}g(x)=g(x_0)且\lim_{u \to u_0}f(u)=f(u_0)且u_0=g(x_0)
x→x0limg(x)=g(x0)且u→u0limf(u)=f(u0)且u0=g(x0)
则
lim
x
→
x
0
f
(
g
(
x
)
)
=
f
(
g
(
x
0
)
)
\lim_{x \to x_0}f(g(x))=f(g(x_0))
limx→x0f(g(x))=f(g(x0))
【证明】
∵
lim
x
→
x
0
g
(
x
)
=
g
(
x
0
)
=
u
0
∵\lim_{x\to x_0} g(x)=g(x_0)=u_0
∵limx→x0g(x)=g(x0)=u0
lim
u
→
u
0
f
(
u
)
=
f
(
u
0
)
\lim_{u \to u_0}f(u)=f(u_0)
limu→u0f(u)=f(u0)
根据复合函数极限定理:
lim
x
→
x
0
f
(
g
(
x
)
)
=
f
(
g
(
x
0
)
)
\lim_{x\to x_0}f(g(x))=f(g(x_0))
limx→x0f(g(x))=f(g(x0))
证毕
7.4、初等函数的连续性
定理:基本初等函数在其定义域内都是连续的,初等函数在其定义区间内是连续的
定义区间:包含在定义域内的区间都叫做定义区间(不唯一)
为什么要说明是定义区间呢?定义域不行吗?
反例:
y
=
cos
x
−
1
y=\sqrt{\cos x-1}
y=cosx−1,这个函数在定义域内是一个一个的点,仅当
cos
x
=
1
\cos x = 1
cosx=1时有定义,但它连续吗?
显然不连续,那么初等函数在定义域内连续就是错误的
而定义区间是一段段的区间不能是点,所以这就限制了上述情况
lim
x
→
0
ln
(
1
+
x
)
x
=
1
\lim_{x \to 0}\frac{\ln(1+x)}{x}=1
limx→0xln(1+x)=1
要证明这个式子我们先要知道一个结论:
若
f
(
x
0
)
f(x_0)
f(x0)在
x
0
x_0
x0处连续,则
lim
x
→
x
0
f
(
x
)
=
f
(
x
0
)
=
f
(
lim
x
→
x
0
x
)
\lim _{x \to x_0}f(x)=f(x_0)=f(\lim_{x \to x_0}x)
limx→x0f(x)=f(x0)=f(limx→x0x)
【证明】
lim
x
→
0
ln
(
1
+
x
)
x
\lim_{x \to 0}\frac{\ln(1+x)}{x}
limx→0xln(1+x)
=
lim
x
→
0
ln
(
1
+
x
)
1
x
=\lim_{x \to 0}\ln(1+x)^{\frac{1}{x}}
=limx→0ln(1+x)x1
=
ln
(
lim
x
→
0
(
1
+
x
)
)
1
x
=
ln
e
=
1
=\ln(\lim_{x \to 0}(1+x))^{\frac{1}{x}}=\ln e=1
=ln(limx→0(1+x))x1=lne=1
证毕
lim x → 0 a x − 1 x = ln a \lim_{x \to 0}\frac{a^x-1}{x}=\ln a limx→0xax−1=lna
【证明】
令
a
x
−
1
=
t
a^x-1=t
ax−1=t
原式
=
lim
t
→
0
t
ln
a
ln
(
1
+
t
)
=
ln
a
=\lim_{t \to 0}\frac{t\ln a}{\ln(1+t)}=\ln a
=limt→0ln(1+t)tlna=lna
证毕
上述式子若 a = e a = e a=e,则 lim x → 0 e x − 1 x = 1 \lim_{x \to 0}\frac{e^x-1}{x}=1 limx→0xex−1=1
8、闭区间上连续函数的性质
8.1、有界性与最大最小值定理
最大最小值定理:设函数 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上连续,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上必有最大值和最小值
而因为有最大和最小值,所以 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上一定是有界的
有界性定理:设函数 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上连续,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上必有界
8.2、零点定理与介值定理
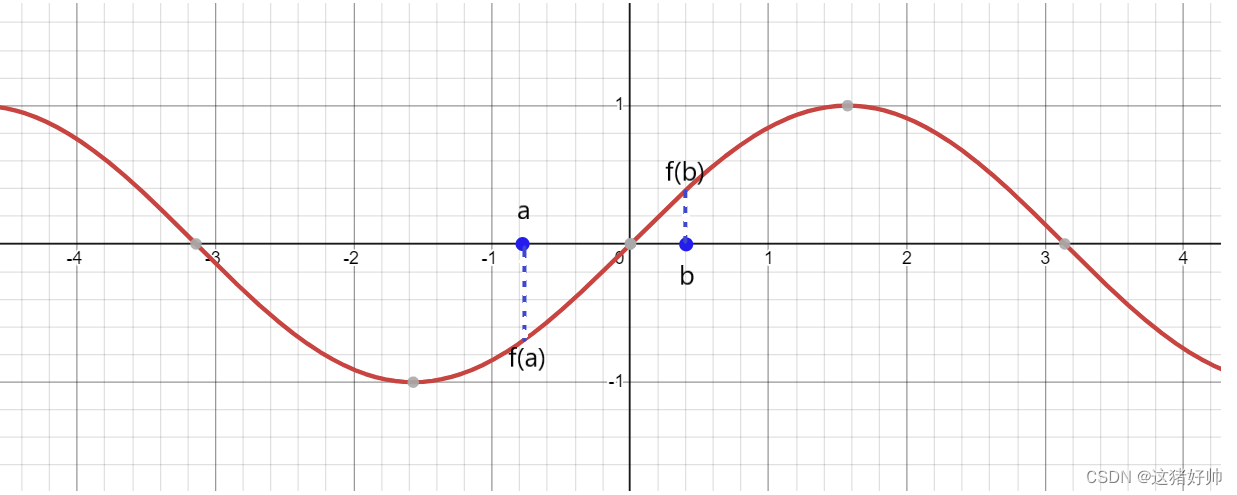
零点定理:设函数 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上连续,且 f ( a ) f ( b ) < 0 , , f(a)f(b)<0,, f(a)f(b)<0,,则 ∃ ξ ∈ ( a , b ) \exist\xi\in(a,b) ∃ξ∈(a,b)使 f ( ξ ) = 0 f(\xi)=0 f(ξ)=0
上述定理从几何上看很明显
如图:
y
=
sin
x
y = \sin x
y=sinx
介值定理:设函数
f
(
x
)
f(x)
f(x)在区间
[
a
,
b
]
[a,b]
[a,b]上连续,且
f
(
a
)
≠
f
(
b
)
,
μ
f(a)≠f(b),\mu
f(a)=f(b),μ为介于
f
(
a
)
f(a)
f(a)与
f
(
b
)
f(b)
f(b)之间的任何值,将至少存在一个
ξ
∈
(
a
,
b
)
\xi\in(a,b)
ξ∈(a,b)使
f
(
ξ
)
=
μ
f(\xi)=\mu
f(ξ)=μ
如图:
我们可以仔细想想,其实介值定理是可以推出零点定理的,因为两个端点
f
(
a
)
,
f
(
b
)
f(a),f(b)
f(a),f(b)异号,而0就是
f
(
a
)
与
f
(
b
)
f(a)与f(b)
f(a)与f(b)之间的一个
μ
\mu
μ
我们再仔细看看上图可以得出如下推论:
设函数
f
(
x
)
f(x)
f(x)在区间
[
a
,
b
]
[a,b]
[a,b]上连续,则
f
(
x
)
f(x)
f(x)在
[
a
,
b
]
[a,b]
[a,b]上能取得介于它的最大值M与最小值m之间的任何值




![[计算机入门] 应用软件介绍(娱乐类)](https://img-blog.csdnimg.cn/e930e2b2ad454f9ba3a36334822cb02b.png)