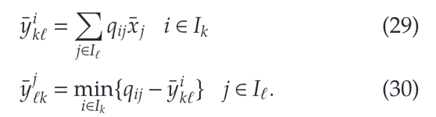论文解读者:范若岭
1. 文章优化问题:
对于下列问题,$ \mathbb{B} = {0, 1}, \mathbb{R} 是实数集合。 是实数集合。 是实数集合。Q 是由实数组成的 是由实数组成的 是由实数组成的n \times n 对称矩阵。 对称矩阵。 对称矩阵。A 是由实数组成的 是由实数组成的 是由实数组成的m \times n 对称矩阵。 对称矩阵。 对称矩阵。c 和 和 和b 分别是长度为 分别是长度为 分别是长度为n 和 和 和m 的实数列向量。其中 的实数列向量。其中 的实数列向量。其中\mathbb{N}= {1, 2, …, n}, I_1, I_2, …, I_k$ 定义了 N \mathbb{N} N的分区,其中索引集合 K = 1 , 2 , . . . , k \mathbb{K} ={1, 2, ..., k} K=1,2,...,k。对于每一个 k ∈ K , I k ⊂ N k \in \mathbb{K}, I_k \subset \mathbb{N} k∈K,Ik⊂N,对于每一对 k , l ∈ K , I k ∩ I l = ∅ k, l\in \mathbb{K}, I_k \cap I_l = \emptyset k,l∈K,Ik∩Il=∅.

1.1 二元二次规划重构为混合整数非线性规划
对于问题
B
Q
P
P
BQP_P
BQPP中的损失函数,可以将其改写成下列形式:

对于任意
i
,
j
∈
I
(
k
)
,
x
(
i
)
x
(
j
)
=
0
i, j \in I(k),x(i)x(j) = 0
i,j∈I(k),x(i)x(j)=0, 因此目标函数的二次部分可以用区分交互成本而不是单个变量的二次成本表示。所以文章引入一个新的连续变量
y
i
k
l
y_{ikl}
yikl,其中
k
,
ℓ
∈
K
,
k
≠
l
,
i
∈
I
(
k
)
k, ℓ \in \mathbb{K}, k \ne l, i \in I(k)
k,ℓ∈K,k=l,i∈I(k)来表示
i
i
i之间的交互成本和
I
l
I_l
Il的分区。
两个分区之间的二次成本可以通过以下公式进行计算。

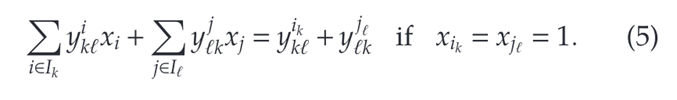
所以,对于二元二次规划的混合整数非线性方程, 其重构形式如下:
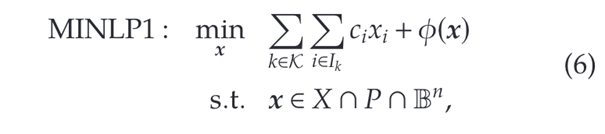
其中,

针对该模型,文章证明了两个理论:
定理一:MINLP1 是 二元二次规划 B Q P P BQP_P BQPP的重新表述.
本文展示如何将 MINLP1转换为凸 MINLP,其中在凸区域和完整性要求的交集上最小化凸目标。为此,我们在连续变量 x ∈ X ∩ P x \in X \cap P x∈X∩P中定义一个新的凸函数 ψ : X ∩ P → R + \psi: X \cap P \to \mathbb{R}^+ ψ:X∩P→R+,描述如下:
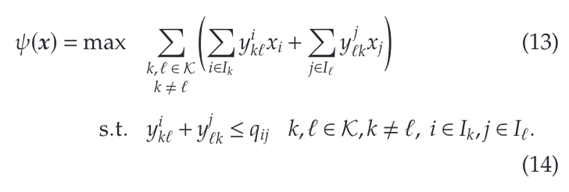
定理二:对于任意一个整数解 x ^ ∈ X ∩ P ∩ B n \hat{x} \in X \cap P \cap \mathbb{B}^n x^∈X∩P∩Bn,都满足 ψ ( x ^ ) = ϕ ( x ^ ) \psi(\hat{x}) = \phi(\hat{x}) ψ(x^)=ϕ(x^)。
根据定理 2,我们可以用 ψ ( x ) , x ∈ X ∩ P ∩ B n \psi(x), x \in X \cap P \cap \mathbb{B}^n ψ(x),x∈X∩P∩Bn代替 MINLP1 中的 ϕ ( x ) \phi(x) ϕ(x),得到如下凸 MINLP:

1.2 二元二次规划重构为混合整数线性规划
对于二元二次规划重构为整数混合线性规划问题,文章主要集中在 RLT (reformulation–linearization technique)的特殊应用方面。RLT全称为重构线性化技术切割,利用切割平面来求解某些二次规划问题以获得最优解。这其中包含两个步骤:1)重构表达式步骤:通过组合原始问题的约束条件从而生成非线性有效不等式,2)线性化步骤:将问题中的每个乘积变成单个的连续变量。因此方程 ( 2 ) (2) (2)将变成一下形式:

上述规划问题将改写成:
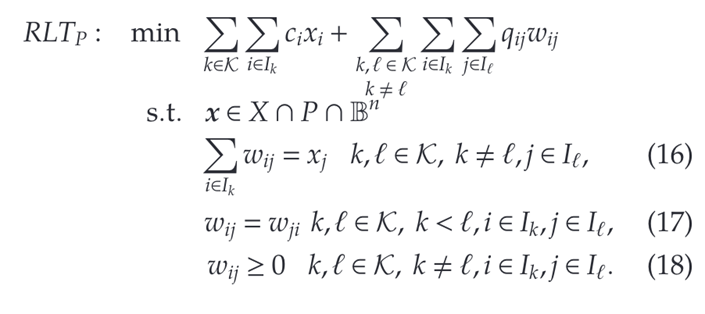
可以证明,
定理三:
R
L
T
P
RLT_P
RLTP是二元二次规划
B
Q
P
P
BQP_P
BQPP的重新表述.
1.3 MINLP2与 RLT P \text{RLT}_P RLTP比较
对于提出的两种等价混合整数模型 MINLP2 \text{MINLP2} MINLP2 和 RLT P \text{RLT}_P RLTP,文章证明了
定理四:假设 C R L T P CRLT_P CRLTP和 C M I N L P 2 CMINLP_2 CMINLP2 分别代表 R L T P RLT_P RLTP和 M I N L P 2 MINLP_2 MINLP2的连续松弛问题.那么 C R L T P CRLT_P CRLTP和 C M I N L P 2 CMINLP_2 CMINLP2是等价的.
2. 算法设计
在介绍了两种混合整数模型之后,文章着重探讨求解混合整数非线性规划MINLP2。
2.1 求解MINLP2: 外近似切平面法
请注意,定义 x 约束足以确保方程可行性; ψ ( x ) \psi(x) ψ(x)是有界的。此外,如果 ( x , η ) (x, \eta) (x,η) 是 MINLP3 的最优解,则 x x x对于 B Q P P BQP_P BQPP 来说是最优的。同时,由于函数 ψ ( x ) \psi(x) ψ(x)是凸函数,并且 MINLP3 的目标函数是线性的,因此问题的最优解始终位于可行集凸包的边界上。这使我们能够使用剖切面技术来解决问题。更准确地说,对于任何给定的(可能是非整数) x ˉ ∈ X ∩ P ⊂ [ 0 , 1 ] n \bar{x} \in X \cap P \subset [0,1]^n xˉ∈X∩P⊂[0,1]n,由于 ψ ( x ) \psi(x) ψ(x)是凸函数,因此可以通过 x ˉ \bar{x} xˉ中的支撑超平面来寻找最优解。令 s ˉ ∈ ∂ ψ ( x ) \bar{s} \in \partial \psi(x) sˉ∈∂ψ(x)为 ψ ( x ) \psi(x) ψ(x)在 x ˉ \bar{x} xˉ处的梯度。然后,根据广义 Benders 分解和外近似,我们可以在一组点 P = { x ˉ 1 , x ˉ 2 , … , x ˉ M } \mathcal{P} = \{\bar{x}_1, \bar{x}_2, \dots, \bar{x}_M \} P={xˉ1,xˉ2,…,xˉM}中对 x ˉ \bar{x} xˉ周围的凸函数 ψ ( x ) \psi(x) ψ(x)进行线性化从而产生以下问题:

如果 M P ( P ) MP(\mathcal{P}) MP(P)包含一组合适的点,则它具有与MINLP2 相同的最优解。因此,外近似算法的主要目标是构建这个等效的MILP。然而,求解 M P ( P ) MP(\mathcal{P}) MP(P)是不切实际的,原因在于必须首先枚举所有可行解 x ˉ ∈ X ∩ P ∩ B n \bar{x} \in X \cap P \cap \mathbb{B}^n xˉ∈X∩P∩Bn。所以,我们通过分支切割算法将求解 M P ( P ) MP(\mathcal{P}) MP(P)转为求解为MILP,其中 (25) 是通过下列过程动态生成的。每一项 ψ ( x ) \psi(x) ψ(x)都是通过求解子问题来计算的。更准确地说,对于 M P ( P ) MP(\mathcal{P}) MP(P)的给定解 x ˉ \bar{x} xˉ,我们用 x = x ˉ x= \bar{x} x=xˉ求解子问题 ψ ( x ) \psi(x) ψ(x),以获得最优解 y y y。因为约束 (14) 与 x ˉ \bar{x} xˉ无关,所以每个 i ∈ N i \in N i∈N 的梯度由下式给出

那么函数的梯度割可以写成,
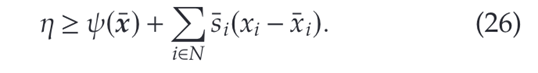
梯度切割 (26) 是沿着分支切割树识别的。从根节点处的一组梯度割开始,在搜索树的每个节点处求解 M P ( P ) MP(\mathcal{P}) MP(P)的线性规划松弛,如果违反则添加梯度切割不等式 (26)。否则,算法将通过对具有非二进制值的二进制变量进行分支来继续进行。
2.2 修正的多切割重构和次梯度计算
鉴于(13)和(14)中定义的函数 ψ ( x ) \psi(x) ψ(x)是可分离的凸函数,我们可以将其重写为每个 k k k的凸函数 ψ k l ( x ) \psi_{kl}(x) ψkl(x)的组合之和 k , l ∈ K , k ≠ l k,l \in \mathcal{K}, k \ne l k,l∈K,k=l,
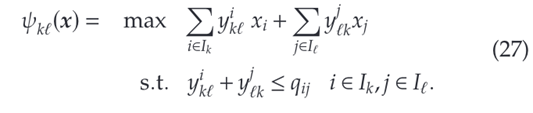
令 y ˉ \bar{y} yˉ为该问题的最优解,并且$\bar{s}{kl} = \sum{i \in I_k}\bar{s}i 是 是 是\psi{kl}(x) 对于每个 对于每个 对于每个k,l \in \mathcal{K}, k \ne l$的梯度。
然后,对于每个 x ˉ ∈ X ∩ P ∩ B n \bar{x} \in X \cap P \cap \mathbb{B}^n xˉ∈X∩P∩Bn,梯度切割 (25) 被替换为

尽管新的梯度割的数量远大于 M P ( P ) MP(\mathcal{P}) MP(P)中的数量,但文中的计算实验表明,分支割算法解决问题实例所需的总体计算时间明显更短。对于每个 k , l ∈ K , k ≠ l k,l \in \mathcal{K}, k \ne l k,l∈K,k=l以及对于任何 x ∈ X ∩ P x \in X \cap P x∈X∩P,子问题 (27)是一个线性程序,可以通过最先进的求解器有效求解。然而,我们可以利用子问题(27)的结构比使用 LP 求解器更有效地获得次梯度割(28):
定理5:
对于 x ˉ ∈ X ∩ P ⊂ [ 0 , 1 ] n \bar{x} \in X \cap P \subset [0,1]^n xˉ∈X∩P⊂[0,1]n,对于每个 k , l ∈ K , k ≠ l k,l \in \mathcal{K}, k \ne l k,l∈K,k=l,(27)的可行解可以通过下列计算得到
此外,如果 x ˉ \bar{x} xˉ是一个整数,那么(29)和(30)可以计算出(27)的最优解。
3. 数值结果
3.1 单一分配 p-Hub 问题
单一分配p_Hub问题可以描述为下列形式:

其中目标函数衡量总运输成本,包括非枢纽-枢纽和枢纽-非枢纽的收集和配送成本以及枢纽到枢纽的传输成本。约束 (32) 强制将每个节点精确地分配给一个中心节点。约束 (33) 规定,如果选择节点 i i i作为集线器,则 k k k只能分配给节点 i i i。约束 (34) 强制开放的枢纽数量为 p p p。为了使用外近似方法,需要定义
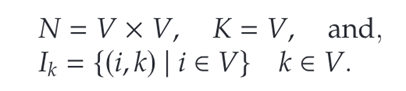
从表1和表2可以看出,文中OABC (outer approxi-mation–based branch-and-cut algorithm)算法在中型到大型实例上的性能非常有前景。当基于主流算法和OABC算法都可以在时限内解决实例的最优问题时,OABC算法大约比主流算法快九倍。此外,OABC算法可以解决所有实例的最优问题,而基于主流算法的 Gurobi 仅解决了 16 个实例中的 8 个。请注意,对于最大的实例,主流算法模型的 LP 松弛问题无法在规定时间内得到可行的解。
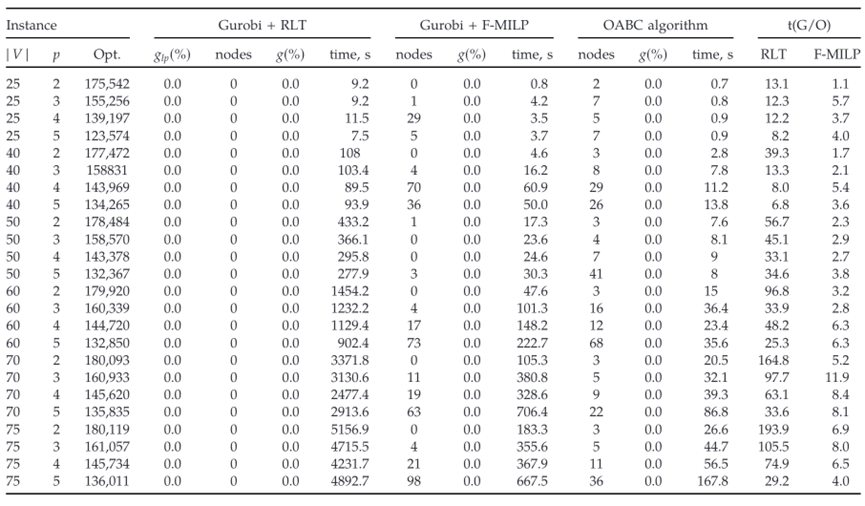
表1: SApHMP 的 AP 数据集的中小型实例上,将基于 RLT 和流的模型与OABC 算法进行比较
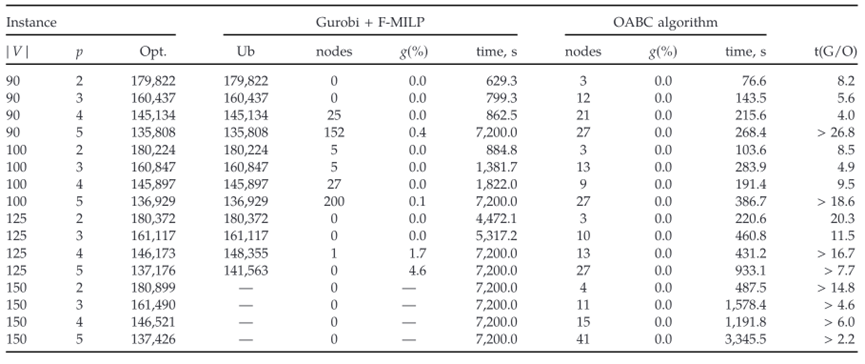
表2: SApHMP 的 AP 数据集的中大型实例上,将基于流的模型与OABC 算法进行比较
3.2 二次半赋值问题(QSAP问题)
有两个集合 V = { 1 , 2 , . . . , p } V=\{1,2,...,p \} V={1,2,...,p}和 M = { 1 , 2 , . . . , m } M = \{1,2, ..., m\} M = {1,2, ..., m},分别由 p p p个对象和 m m m个位置组成。令 c i k c_{ik} cik表示将对象 k ∈ V k \in V k∈V分配给位置 i ∈ M i \in M i∈M的成本, q i j k l q_{ijkl} qijkl表示同时将对象 k k k分配给位置 i i i和对象 l l l分配给位置 j j j的成本。二次半分配问题寻求以最小的总成本将每个对象精确地分配到一个位置。在这里,如果对象 k ∈ V k \in V k∈V被分配到位置 i ∈ M i \in M i∈M,我们定义二元变量 x i k x_{ik} xik等于1,否则定义为零,以获得以下二元二次公式:
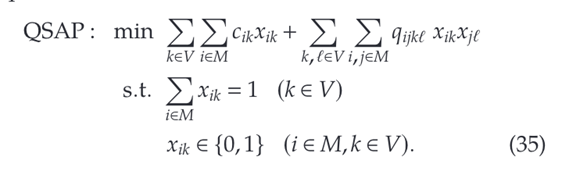
为了使用外近似方法,定义

从表4和表5中我们可以看出,本文中的OABC算法在整体计算时间方面有明显优势;当两种方法都可以在规定时间内解决实例的最优问题时,OABC算法的速度大约是原来的六倍。此外,OABC算法可以解决所有实例的最优性,而对于C01类的最大实例,Gurobi 达到了两个小时的时间限制,最优性差距为 2.9 % 2.9 \% 2.9 %。
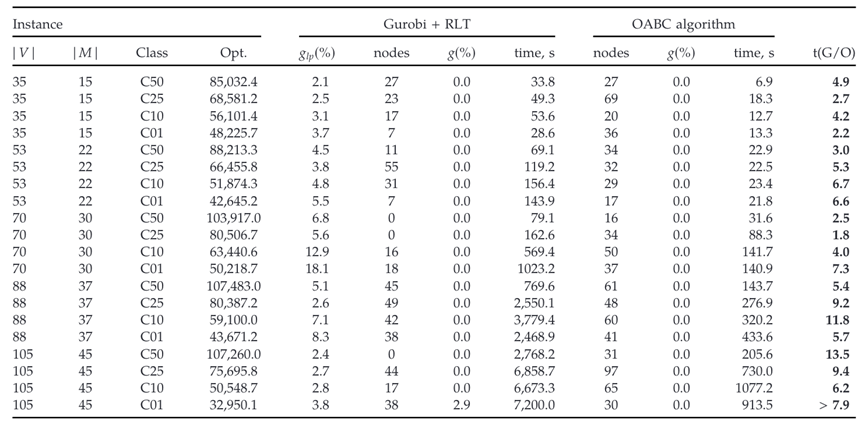
表4: 在一组随机生成的 QSAP 实例上基于 RLT 的模型与本文OABC算法进行比较的结果
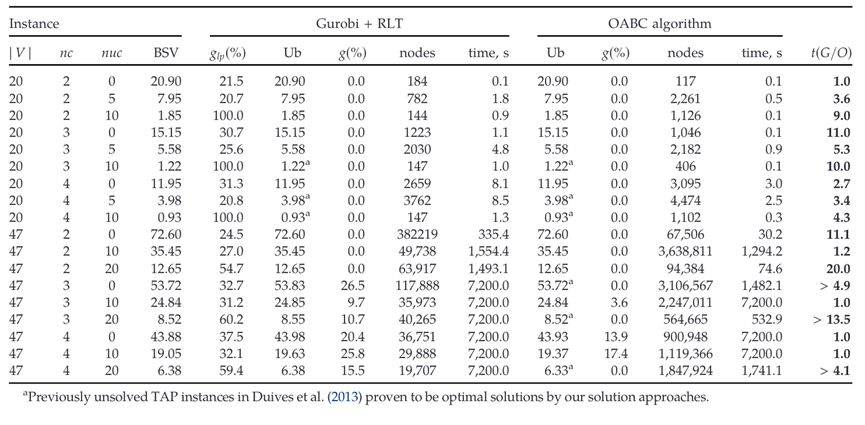
表5: 真实 TAP 实例上基于 RLT的模型与本文算法比较