https://www.luogu.com.cn/problem/CF1592F2

做完F1，然后用1的结论来思考。

场上推了几个性质。首先op4的操作行列必然两两不同，所以op4最多 $\max (n,m)$ 次。然后手玩发现只有除 $(n,m)$ 的三个格子都为1，op4才有意义。

然后猜了个网络流。每个点如果满足条件，就向行列连边。

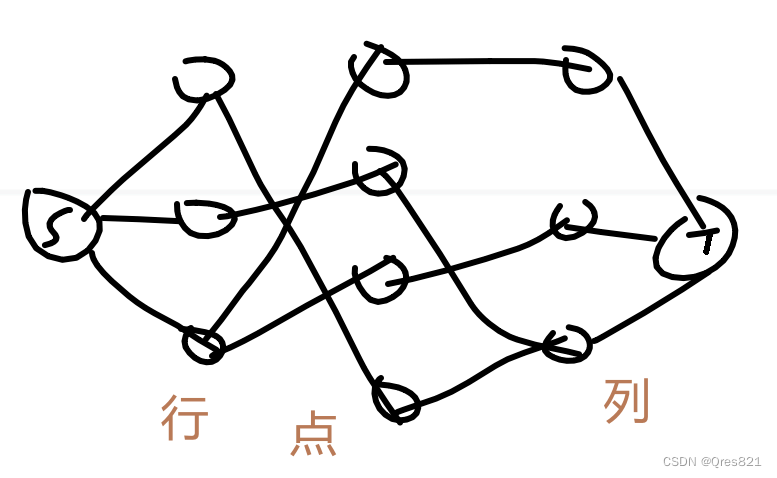
但这样显得我非常愚蠢。

因为中间的点完全没用，直接行向列连边就变成二分图了…

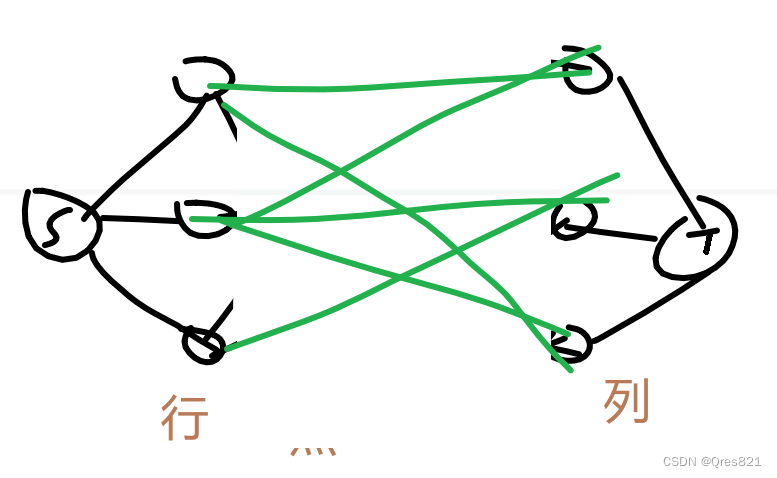
	auto calc = [&] (int x, int y) -> int {
		return a[x][y]^a[x+1][y]^a[x][y+1]^a[x+1][y+1]; 
	}; 
	mf_graph<int>G(N*N); 
	n=read(); m=read(); 
	for(i=1; i<=n; ++i) {
		scanf("%s", str+1); 
		for(j=1; j<=m; ++j) 
			if(str[j]=='B') a[i][j]=1; 
	}
	for(i=n; i>=1; --i) 	
		for(j=m; j>=1; --j) {
			v[i][j]=calc(i, j); sum+=v[i][j]; 
	}
	S=n+m+1; T=S+1; 
	for(i=1; i<n; ++i) if(v[i][m]) G.add_edge(S, i, 1); 
	for(i=1; i<m; ++i) if(v[n][i]) G.add_edge(i+n, T, 1); 
	for(i=1; i<n; ++i)
		for(j=1; j<m; ++j) 
			if(v[i][j] && v[n][j] && v[i][m]) G.add_edge(i, j+n, 1); 
	k=G.flow(S, T); p=v[i][j]; v[i][j]^=(k&1); 
//	printf("%d %d\n", sum, k); 
	ans=min(sum, sum-k-p+v[i][j]); 
	if(v[i][j] && k) ans=min(ans, sum-(k-1)); 
	printf("%d", ans);