目录
1. 什么是APT?
2. APT 的攻击过程?
3. 详细说明APT的防御技术
4. 什么是对称加密?
5. 什么是非对称加密?
6. 私密性的密码学应用?
7. 非对称加密如何解决身份认证问题?
8. 如何解决公钥身份认证问题?
9. 简述SSL工作过程
1. 什么是APT?
APT攻击---高级可持续威胁攻击,也称为定向威胁攻击,指某组织特定对象展开得持续有效的攻击活动。集合了多种常见攻击方式得综合攻击,综合多种攻击途径来尝试突破网络防御。是黑客以窃取核心资料为目的,通过Web或者电子邮件,利用应用程序或操作系统得漏洞,针对客户所发动得网络攻击和侵袭行为,隐匿自己,针对特定对象有计划、长期和组织地窃取数据,这种发生在数字空间得偷窃资料,搜集情报得行为。
2. APT 的攻击过程?
第一阶段:扫描探测,攻击者通过长期得潜伏,对“目标”网络进行踩点,针对性得收集信息,和网络环境探测,
第二阶段:工具投送,攻击者通过邮件得方式,诱骗让其“目标”点开恶心软件或连接,然后利用常见软件的0day漏洞,投送其恶意代码,伪装自己,避开扫描,通过长期的潜伏,恶意代码在一台主机等设备里,或通过云的文件共享来感染一台主机,并在网络中横向传播。
第三阶段:漏洞利用,攻击者通过投送恶意代码,并利用目标企业使用的软件中漏洞执行自身。而如果漏洞利用成功的话,将感染你的系统,
第四阶段:木马植入,一旦漏洞利用成功,攻击者就已经从组织防御内部建立一个控制点,攻击者最常用的就是远程控制工具。通过远程控制工具反向连接模式建立,其目的就是允许从外部控制员工电脑或服务器,即这些工具从位于中心的命令和控制服务器接受命令,然后执行命令,而不是远程得到得命令,这种连接方式是难以检测,因为普通得主机是主动与命令和控制服务器通信而不是相反。
第六阶段:横向渗透,攻击者首先突破得员工个人电脑并不是攻击者感兴趣的,它感兴趣的组织内部其他包含重要资产的服务器,因此攻击者先以内部个人主机为跳板,然后在内部系统中横向渗透,以攻击更多的主机和服务器。攻击者采取的横向渗透方法包括口令窃取和漏洞攻击等
第七阶段:目标行动,将敏感数据从被攻击的网络非法传输到由攻击者控制的外部系统,发现有价值的数据,APT攻击往往将这些数据收集到一个文档,然后将文档压缩并加密,此操作将隐藏内容,放置遭受深度的数据包检测和DLP技术的阻止,
3. 详细说明APT的防御技术
APT的防御技术,目前使用的是最有效的方法是沙箱技术,通过沙箱技术构造一个隔离的威胁检测环境,然后将网络流量送入沙箱进行隔离和分析并给出最终是否存在威胁的结论,如果沙箱检测到某流量为恶意流量,则可以通知防火墙实施阻断。总体来说,反病毒系统是以被检测对象的特征来识别攻击对象,APT防御系统是以被检测对象的行为来识别攻击对象。
4. 什么是对称加密?
对称加密也称为单钥加密,加解密都是用的同一个密钥,从数学角度是一个双向函数,对称加密首先要保证算法足够复杂以及密钥传输足够安全,其特点是算法公开、加密速度快,加密效率高,计算量小,缺点就是一旦将密钥泄露,别人就可以对密文进行解密。常用对称加密算法有DES、AES等。
5. 什么是非对称加密?
非对称加密也被称为公钥加密技术,加解密使用的密钥是不同的,分为公钥和私钥。公钥和私钥形成一个密钥对,其中公钥向公众公开,私钥归密钥持有人单独保管。通讯双方使用非对称密钥对数据进行加密和解密时,必须使用相互匹配的公钥和私钥。它有两种方式:一种是发送方用接收方的公钥来加密信息,接收方用其私钥解密信息,这样接收方可以收到多个发送方传来的加密数据,且此加密数据只有接收方一个用户可以解读;另一种即发送方利用自身的私钥加密信息,接收方用对方公钥解密信息,这样一个信息有可能被多个接收方解密。其特点速度慢、但是安全。如果窃取者只获取其中私钥或者公钥,是无法解密的。常用非对称加密算法RSA、ECC等。
6. 私密性的密码学应用?
对称加密:对称加密算法使用相同的密钥对数据进行加密和解密,可以确保加密数据只能被知道密钥的用户解密。常见的对称加密算法包括AES、DES等。
非对称加密:非对称加密算法使用不同的密钥对数据进行加密和解密,其中一个密钥是公开的(公钥),而另一个密钥是私有的(私钥)。这种算法可以确保加密数据只能被知道私钥的用户解密。常见的非对称加密算法包括RSA、ECC等。
散列函数:散列函数可以将任意长度的数据转换为固定长度的散列值,这个散列值通常用于验证数据的完整性和真实性。只有知道原始数据的用户才能生成相同的散列值。常见的散列函数包括MD5等。
数字签名:数字签名是通过使用私钥对数据进行签名来验证其完整性和真实性的一种机制。数字签名可以确保数据没有被篡改或者被其他人伪造,只有知道私钥的用户才能进行签名。常见的数字签名算法包括RSA、DSA等。
7. 非对称加密如何解决身份认证问题?
有两把密钥,一个公开得公钥,一个非公开的私钥
公钥和私钥一一对应,有一把公钥就必然有一把与之对应的、独一无二的私钥,反之也成立
同时生成公钥和私钥应该相对比较容易,但是从公钥推算出私钥,应该是很困难或者是不可能的
所有的秘钥对(公钥,、私钥)都是不同的
用公钥可以解开私钥加密的信息,反之也成立
例如:
发送者是alice,使用非对称算法,生成私钥A,公钥B。
1. alice把公钥给bob
2. alice发送信息hello,world!
3. alice把发送的信息用对称加密算法加密到加密信息C。
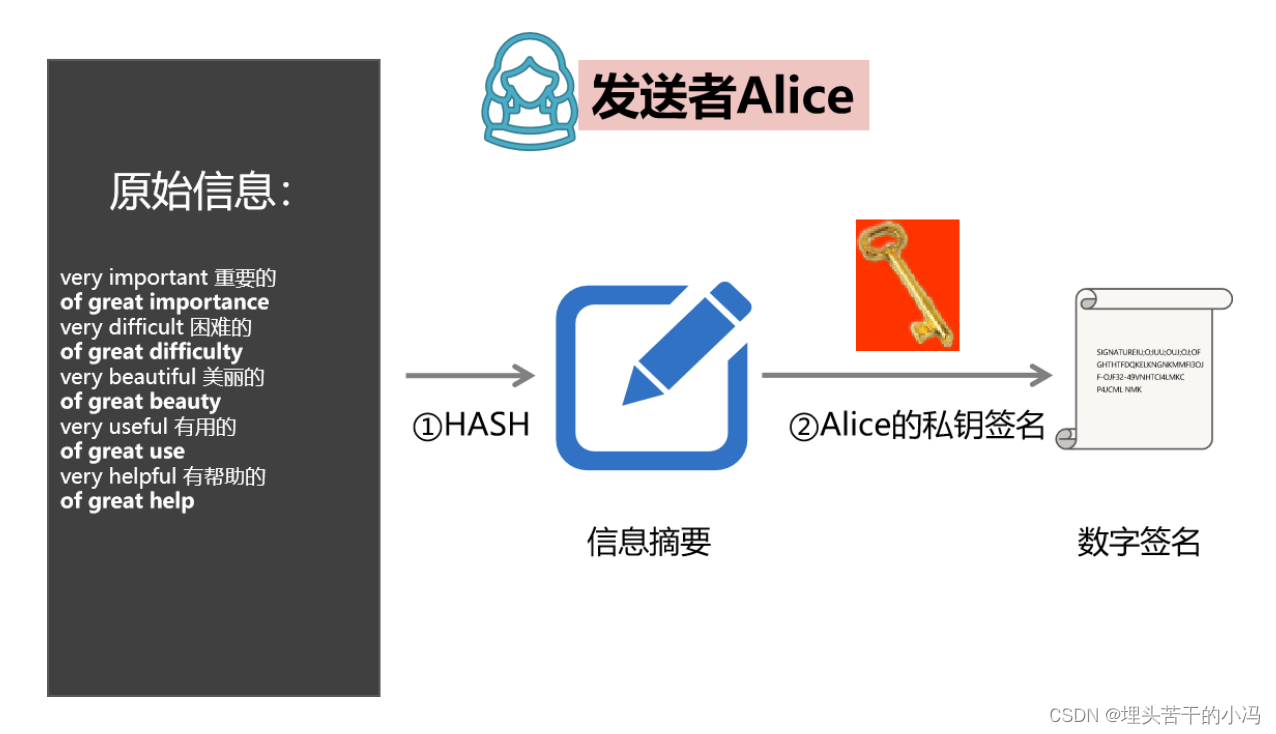
4. alice把发送的hello,world!先用hash算法计算得到hash值D。
5. alice把hash值D用非对称加密计算得到E。E值就是用于身份验证的。
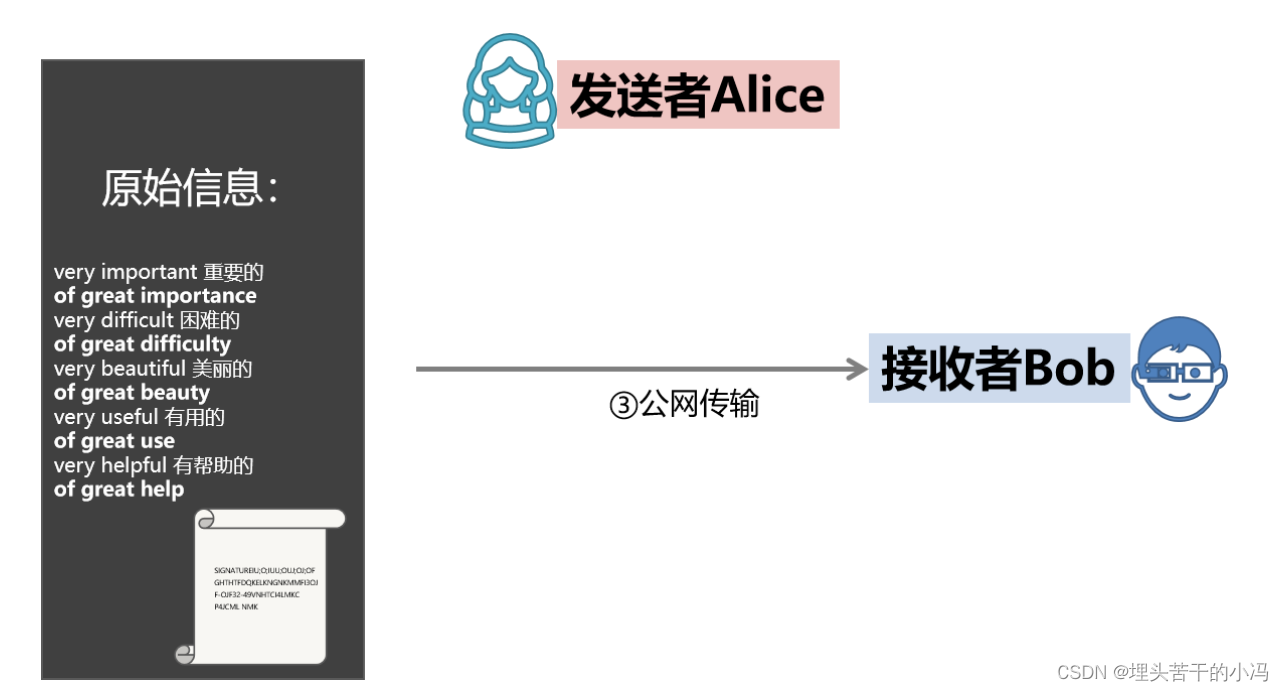
6. alice把C、E一起发给bob。
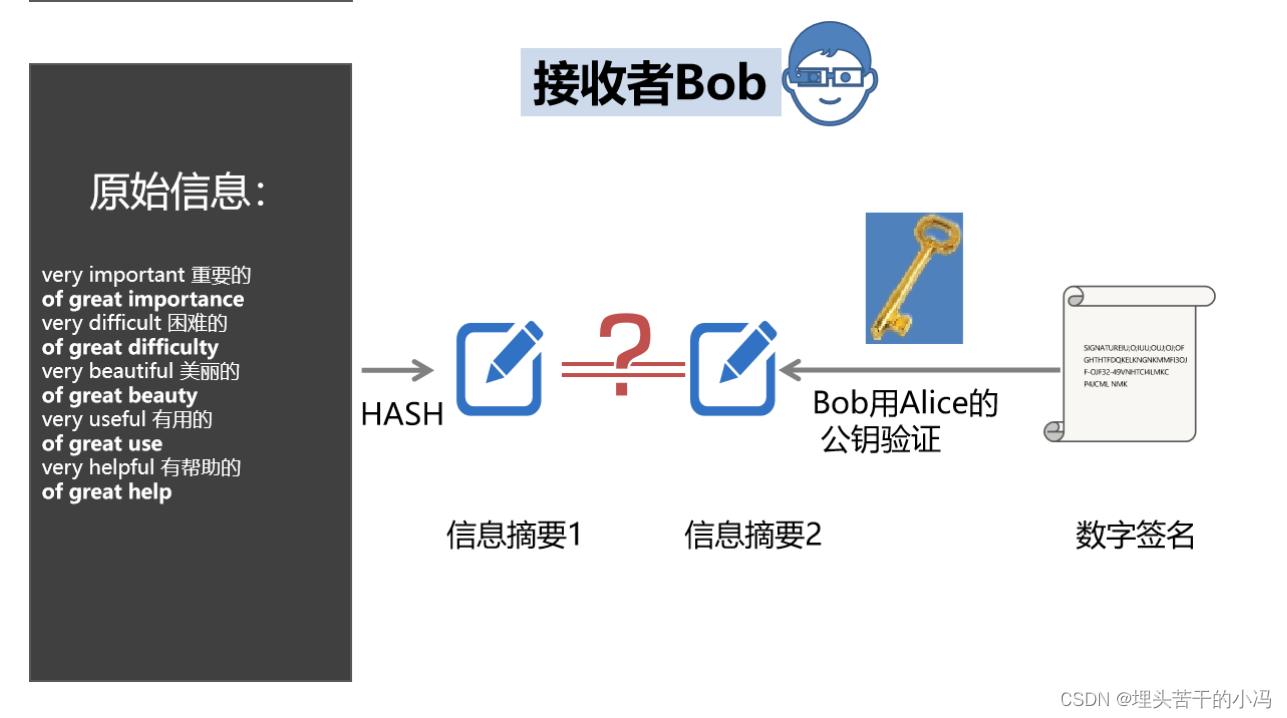
7. bob收到C、E值,先用非对称的公钥对E进行解密,如果能正常解开则证明C值是alice的。
8. 如何解决公钥身份认证问题?
上题述1中如果黑客偷换了alice的公钥,那么就会出现身份认证漏洞。
解决:
alice把公钥给bob的环节能确保是安全的,一定是alice给的。
想办法证明alice的公钥一定是alice的。
公钥的“身份证”-----数字证书
9. 简述SSL工作过程
1、无客户端认证的握手过程
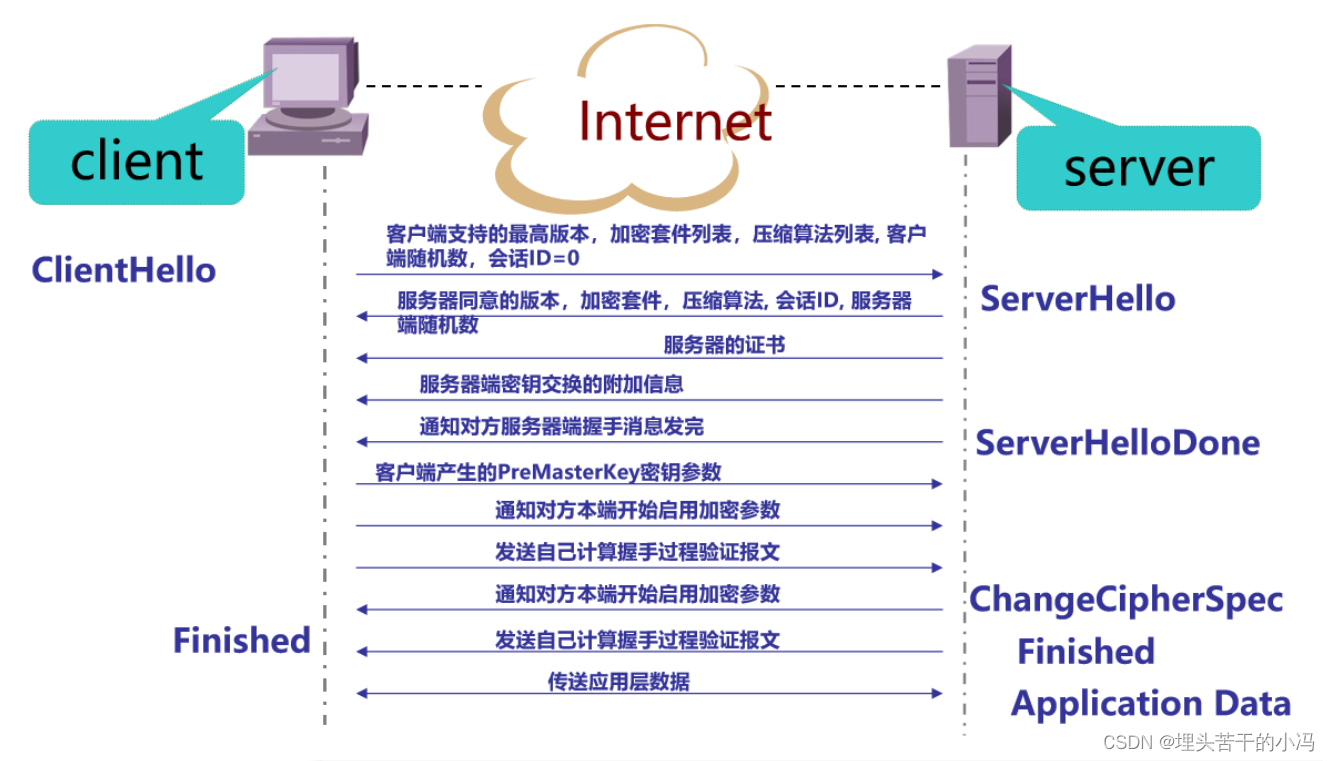
2、有客户端认证的握手过程
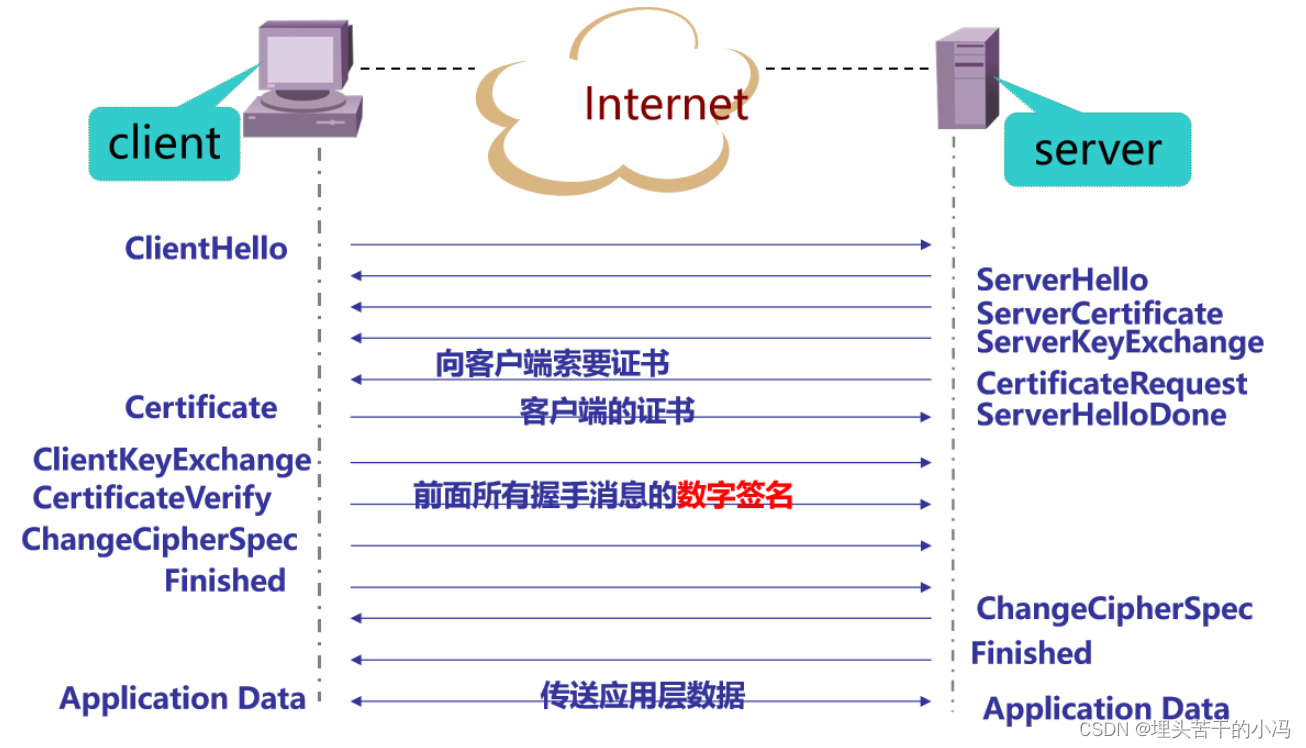
3、会话恢复过程