文章目录
- 前言
- 数字统计专题
- 符号统计
- 阶乘0的个数
- 溢出问题
- 整数反转
- 字符串转整数
- 回文数
- 进制专题
- 七进制数
- 进制转换
- 总结
前言
提示:生活是正着来生活,倒着去理解。 --戴维·迈尔斯《社会心理学》
数学是学生时代掉头发的学科,那算法是毕业后掉头发的学科。那么如果两者相遇,你会不会更头疼,其实很多算法本身就是数学问题,而且很多数学问题也需要借助算法才能用代码实现。数学的门类有很多,也涉及到很多问题。很多都是相当难的题目。但是在算法中,一半只会选择各个学科中的基础问题来考察,例如素数问题,幂、对数、阶乘、幂运算、初等代数、几何问题、组合数学等待。本次就来讨论一下这些热门的话题。
数字统计专题
统计一下特定场景下的符号,或者数字个数等是一类非常常见的问题。如果按照正常方式去统计,可能会非常复杂,所以有必要掌握一些技巧。
符号统计
参考题目介绍:1822. 数组元素积的符号 - 力扣(LeetCode)


你看下这个题目,如果将所有的数都乘起来,在判断正负的话,工作量真的可以了,还要考虑溢出问题。但是换个思路,如果我们只统计负数的个数呢?是不是就能够判断最后乘积的正负(符号了呢?
/**
* 数组元素乘积的符号
* @param nums
* @return
*/
public static int arraySign(int[] nums) {
int sign = 1;
for(int i = 0; i < nums.length; i++) {
// 出现 0 就直接返回
if (nums[i] == 0){
return 0;
}else if (nums[i] < 0){
sign = -sign;
}
}
return sign;
}
阶乘0的个数
参考题目地址:面试题 16.05. 阶乘尾数 - 力扣(LeetCode)

这个题如果硬算,我想也很是头疼,题目的重点是计算有多少个0.转化一下,是计算有多少个2和5一起出现,当然2的次数要大于5的次数,因此我们只需要检查5出现的次数就可以了,那么我们在统计的过程中,我们只需统计5,10,15,25,… 5 * n 这样的整数倍就可以了。然后在累加起来,就知道有多少个0。
代码可以这样写😎:
/**
* 阶乘尾数0的个数
* @param n
* @return
*/
public static int trailingZeroes(int n) {
int cnt = 0;
for(long num = 5; n / num > 0; num*=5){
cnt += n / num;
}
return cnt;
}
这个也可以简化求5因子的个数哈哈🤣
数学不仅与算法难以区分,很多算法问题还与位运算密不可分,有些题目真的不好说是不是倍错分了。我们就一块看看吧。
溢出问题
溢出问题是一个极其重要的问题,只要涉及到输出一个数字,都可能遇到,典型的题目有三种:
- 数字反转
- 将字符串转成数字
- 回文数
不过溢出问题也不会单独考察,面试官也不会提醒你,但是你需要留意是不是的陷阱,凡是涉及到输出结果为数字的,需要考虑数学的特有问题。(溢出☠️)
溢出处理的技巧都是一致的,我们学习一下。
整数反转
参考题目地址:7. 整数反转 - 力扣(LeetCode)


这个题的关键点有两个:
- 怎么反转
- 如何处理溢出
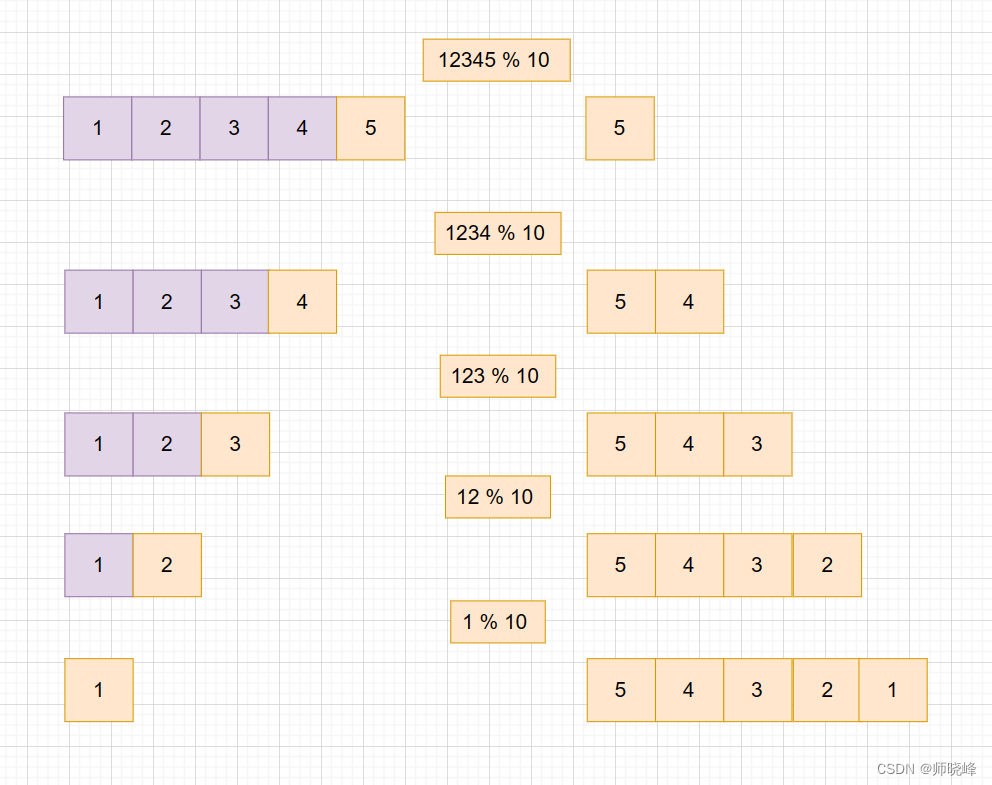
反转:用栈 不不不,或者将整数转字符串? 不不不。 我们只需要一边左移一边处理末尾数字就可以了。就比如12345。 我们要的是54321。(可以循环取模解决)
12345 54321
12345 % 10 = 5 12345 / 10 = 1234 (5)
1234 % 10 = 4 1234 / 10 = 123 (54)
123 % 10 = 3 123 / 10 = 12 (543)
12 % 10 = 2 12 / 10 = 1 (5432)
1 % 10 = 1 1 / 10 = 0 (54321)
画图就是这样:
这样的话,是不是将循环的判断条件改为x > 0 就可以了呢? 当然不行(负数呢?) 应该是while(x != 0)。去掉符号,剩下的数字,无论是正数还是负数,按照上面的不到 / 10 这样的操作,最终都会变成0,所以判断终止条件就是 != 0。有了取模和除法操作就可以解决第一个反转问题。
那么怎么处理溢出呢? 这里就要考虑到32为最大整数时MAX=2147483647,如果一个整数num > MAX,那么就应该由一下规律:
- num / 10 > MAX / 10 = 214748364 (也就是说倒数第二位 大于4,不管是什么都会溢出)
如图:
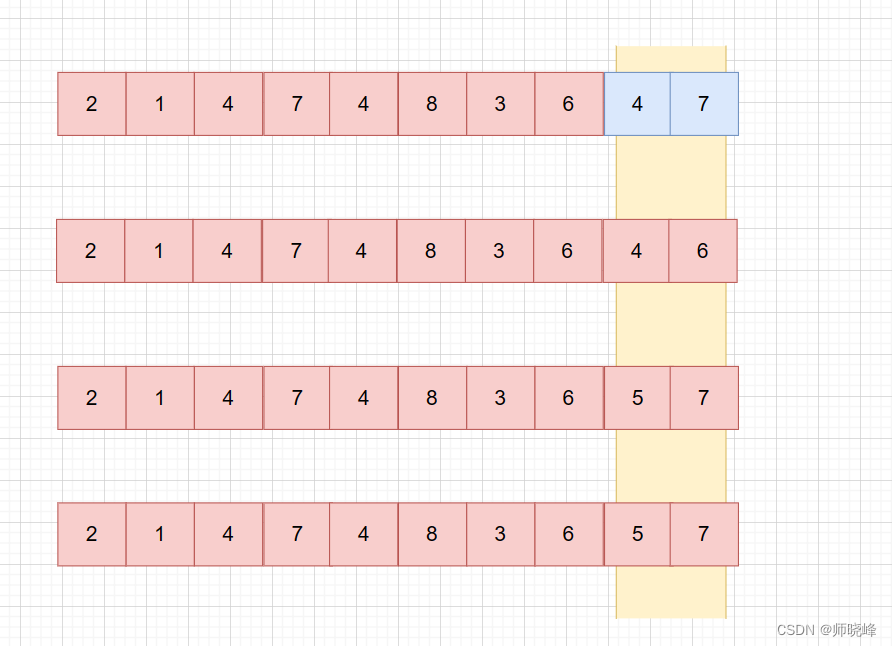
所以这里从倒数第二位就开始判断了,
- 如果 num > 214748364 后面就不用判断了,必定溢出
- 如果 num = 214748364 需要判断最后一个位数是否大于 7,比7大说明溢出了。
- 如果 num < 214748364 没问题,可以继续处理。
对于负数也是一样,所以代码可以这样写:
/**
* 整数反转
* @param x
* @return
*/
public static int reverse(int x) {
int res = 0;
// 注意条件
while (x != 0) {
// 获取最后一个余数
int temp = x % 10;
// 判断是否溢出
// 正数溢出
if (res > 214748364 || res == 214748364 && temp > 7) {
return 0;
}
if (res < -214748364 || res == -214748364 && temp < -8) {
return 0;
}
res = res * 10 + temp;
x /= 10;
}
return res;
}
当然这里也可以使用 Integer.MAX_VALUE / 10 代替
字符串转整数
参考题目地址:8. 字符串转换整数 (atoi) - 力扣(LeetCode)
这道题我们在字符串章节已经做过了,但是再回顾一下是不是,有理解了很多。请参考看:算法通过村第十二关-字符串|青铜笔记|隐形的王者-CSDN博客

public int myAtoi(String s) {
int index = 0;
char[] chars = s.toCharArray();
int n = chars.length;
// 1.丢掉无用的空格
while(index < n && chars[index] == ' '){
index++;
}
// 排除一些特殊情况
if (index == n){
return 0;
}
// 3.这里记录正负数
int sign = 1;
char characterOps = chars[index];
if (characterOps == '+'){
index ++;
}else if (characterOps == '-'){
index ++;
sign= -1;
}
int res = 0;
// 4.继续循环
while(index < n){
char currChar = chars[index];
// 4.1 判断是否合法
if (currChar < '0' || currChar > '9'){
break;
}
// 4.2 判断溢出问题
if (res > Integer.MAX_VALUE / 10 || res == Integer.MAX_VALUE / 10 && (currChar - '0')> Integer.MAX_VALUE % 10 ){
return Integer.MAX_VALUE;
}
if (res < Integer.MIN_VALUE / 10 || res == Integer.MIN_VALUE / 10 && (currChar - '0') > -(Integer.MIN_VALUE % 10) ){
return Integer.MIN_VALUE;
}
res = res*10 + sign*(currChar - '0');
// 注意index 变化
index ++;
}
return res;
}
回文数
参考题目介绍:9. 回文数 - 力扣(LeetCode)


思考如何利用数字特性呢?
第一个想到的是不是上面的转字符串哈哈🤣,然后再检查是不是回文。但是,需要这里增加了额外空间和题目描述不一样。
换一种思路,那我们将数字本身反转,然后将反转后的数字与原始数字进行比较,如果他们时相同的,那么这个数字就是回文。但是如果这个数字反转后溢出了,就属于一出问题了。
接着这个想法:为了避免溢出,我们可以考虑int数字的一半,回文数字嘛,后半部分和前半部分时一样的。
例如:输入1221,我们可以将数组1221 后半部分21 转成 12 并和前半部分比较如果反转后一样就说明回文了。
这个反转思路与链表反转一样的,请参考:算法通过村第二关-链表青铜笔记_师晓峰的博客-CSDN博客,思路一样的。
这里还不能忘记的问题就是,反转之后数字肯会溢出,因此必须要做防护,根据上面的方法我们写一下代码:
/**
* 方法2:通过移位计算
*
* @param x
* @return
*/
public static boolean isPalindrome2(int x) {
if(x < 0){
return false;
}
long res = 0;
int old = x;
while(x > 0){
res = res * 10 + x % 10;
x /= 10;
}
return res == old;
}
折半(数字)
/**
* 折半查找
* @param x
* @return
*/
public static boolean isPalindrome3(int x) {
// 特殊情况处理
// 如果 负数 不可能
// 同样的 如果最后移位是0 为了回文数字的第一位也得是0
// 所以这一样 只有0满足条件
if(x < 0 || (x % 10 == 0 && x != 0)){
return false;
}
int revertedNumber = 0;
while(x > revertedNumber){
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时 采用 x == revertedNumber / 10
// 当数字长度为偶数时 采用 revertedNumber == x
return revertedNumber == x || x == revertedNumber / 10;
}
进制专题
进制问题也是一个非常重要的专题,有的直接处理还挺费劲的,我们看看下面这些题目。
七进制数
参考题目介绍:504. 七进制数 - 力扣(LeetCode)

我们可以先想想二进制的特征,迁移一下7进制数的。在二进制中,先是 0 ,然后 1。而 2 就是 10(2),3就是11(3) 一次类推。同样在7进制中,计数应该是这样的:
0 1 2 3 4 5 6 10 11 12 13 14 15 16 …
所以 7 进制主要过程也是循环取余和整除【特色】,最后将所有的余数反过来就行了。
例如:将10进制数100转换为七进制:
100 % 7 = 14 余数 2
14 % 7 = 2 余数 0
2 % 7 = 0 余数 2
向遍历每次的余数,一次是202因此十进制的100 转成七进制就是202。如果num < 0,则先对 num 取绝对值,然后再转换即可。使用代码同样可以实现该过程,需要注意的十如果单纯按照整数来处理会非常麻烦,既然题目说以字符串形式返回,那么这直接用字符串类。代码如下:
/**
* 七进制转换
* @param num
* @return
*/
public static String convertToBase7(int num) {
StringBuilder sb = new StringBuilder();
// 先确定到正负号
boolean sign = num < 0;
if (sign) {
num *= -1;
}
// 循环取余和整数
do{
sb.append(num % 7 + "");
num /= 7;
}while(num > 0);
// 添加符号
if (sign) {
sb.append("-");
}
// 这里需要反转一下
StringBuilder res = reverse(sb,0,sb.length() - 1);
return res.toString();
}
public static StringBuilder reverse(StringBuilder sb, int start, int end) {
while(start < end){
char temp = sb.charAt(start);
sb.setCharAt(start++,sb.charAt(end));
sb.setCharAt(end--, temp);
}
return sb;
}
进制转换
给定一个十进制M,以及需要转换的进制数N,将十进制数M转换为N进制数。M是32位整数,2 <= N <= 16。
这个题目思路不复杂,但是想写却很不容易,甚至越写越糊涂。本题有好几个需要处理的问题:
- 超过进制最大范围之后如何准确映射到其他进制,特别是ABCDEF这种情况。简单的方式是大量采用if判断,但是这样写就一直往下写,就成一坨了。
- 需要对结果进行一次转置。
- 需要判断符号。
下面这个是我总结出的最精简,最容易理解的实现方案。注意采取三个措施来方便处理:
- 首先定义大小为16 的数组F,保存的是2到16的各个进制的值对应的标记,这样赋值计算只需要处理下标,不必考虑不同进制之间的转换问题。
- 使用 StringBuffer 完成数组转置等功能,如果不采用这个思路,工作量直接飙升。
- 通过一个 flag 来判断正数还是负数,最后才处理。
/**
* 将十进制数M转化为N进制数
*
* @param M
* @param N
* @return
*/
public static String convert(int M, int N) {
// 首先先判断正负
boolean flag = false;
if (M < 0){
flag = true;
M *= -1;
}
StringBuffer sb = new StringBuffer();
int temp;
// 注意条件
while(M != 0){
temp = M % N;
// 技巧一:通过数组F[] 解决了大量繁琐的不同进制之间映射的问题
sb.append(F[temp]);
M = M / N;
}
// 技巧二:使用 StringBuffer 的 reverse() 方法,让原本麻烦的转置瞬间就美好
sb.reverse();
// 技巧三:最后处理正负,不要从一开始就揉在一起
return (flag ? "-" : "")+sb.toString();
}
总结
提示:数学与数字;统计专题;溢出问题;进制转换;反转问题
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。