一、问题描述：

传送门：[洛谷]P1449 后缀表达式

题目描述

所谓后缀表达式是指这样的一个表达式：式中不再引用括号，运算符号放在两个运算对象之后，所有计算按运算符号出现的顺序，严格地由左而右新进行（不用考虑运算符的优先级）。

如：$\text{3*(5-2)+7}$ 对应的后缀表达式为：$\text{3.5.2.-*7.+@}$。在该式中，@ 为表达式的结束符号。. 为操作数的结束符号。

输入格式

输入一行一个字符串 $s$，表示后缀表达式。

输出格式

输出一个整数，表示表达式的值。

样例 #1

样例输入 #1

3.5.2.-*7.+@

样例输出 #1

16

提示

数据保证，$1\le |s|\le 50$，答案和计算过程中的每一个值的绝对值不超过 $10^9$。

二、思路分析

1、算法标签

这道题考察的是二叉树的后序遍历，以及数据结构栈的使用。

2、思路

很多人会感到疑惑，为什么这道题考察的是二叉树的后序遍历呢？我们不妨将这道题的输入转换为一颗二叉树。

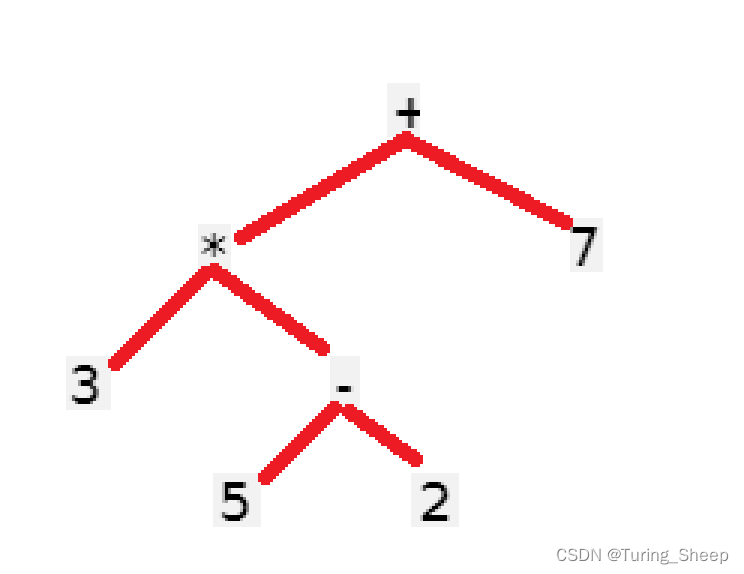
那么我们对这棵树根据：左子树–>右子树—>根的顺序进行遍历，我们会得到如下的式子：

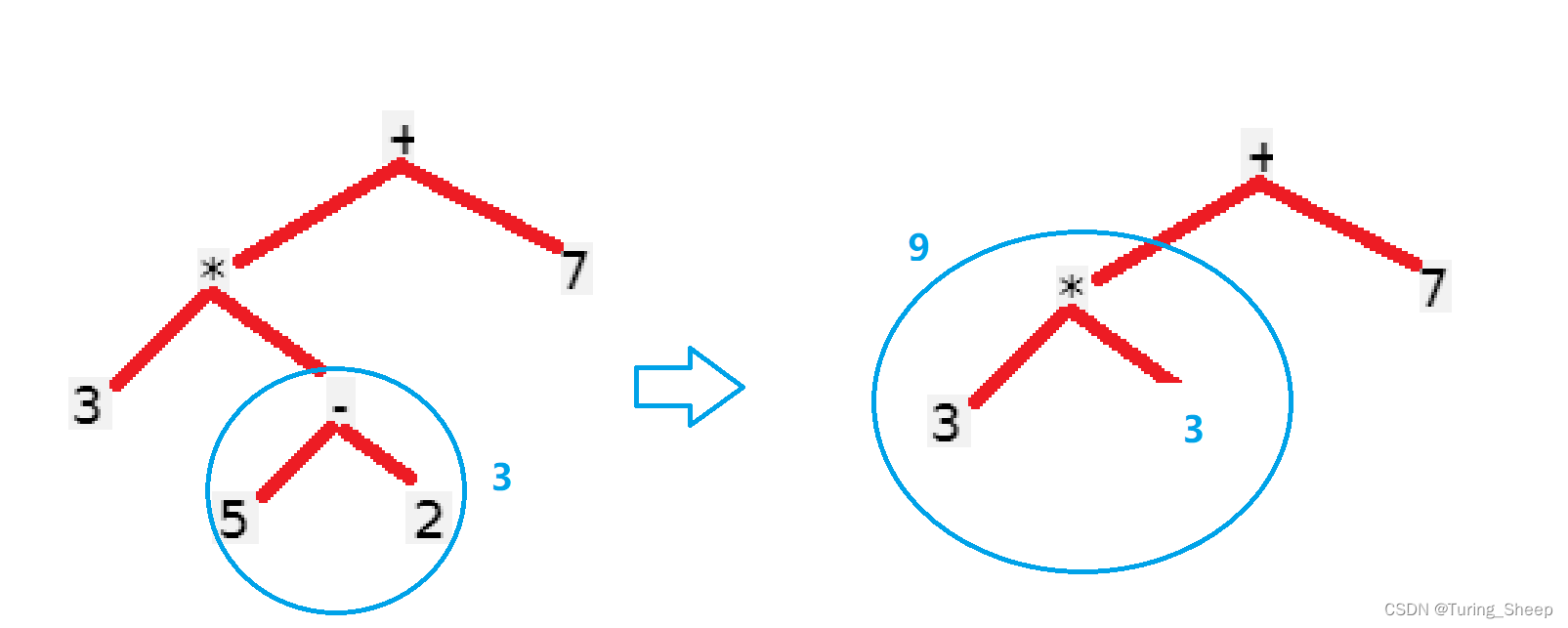
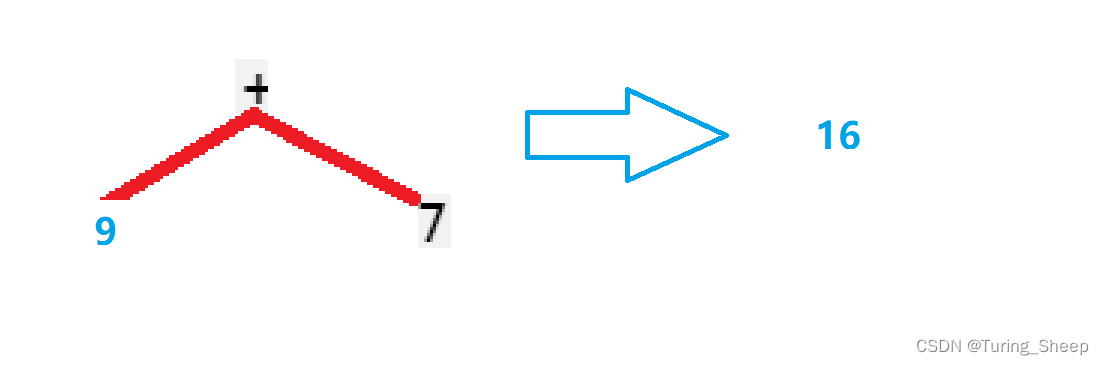
我们发现进行后序遍历后，就会得到我们的最终结果。

而我们后序遍历依次得到的是：

5，2，-
3，3，*
9，7，+

我们会发现，只要遇到符号，就将该符号前面的数字拿出来计算。
而且我们拿出来的数据不是最先加进去的，而是运算符前面的后进的数据。而这种后进先出的特点恰好符合数据结构中栈的特点。

因此，我们使用栈来解决这个问题。

我们创建一个栈$stk$来存储数字。

我们读取字符串，读到数字的话，我们就让这个数字进入$stk$中，每当读到字符的时候，我们就从$stk$中取出两个栈顶元素，进行运算。然后，我们再将运算的结果放回栈中。

最终当所有的运算都结束后，我们的$stk$中应当仅仅剩余一个元素。而这个元素就是我们的最终答案。

三、代码实现

#include<iostream>
#include<stack>
using namespace std;
stack<int>stk;
int cal(char a)
{
    int t1=stk.top();
    stk.pop();
    int t2=stk.top();
    stk.pop();
    if(a=='+')return t2+t1;
    else if(a=='-')return t2-t1;
    else if(a=='*')return t2*t1;
    else return t2/t1;
}
int main()
{
    string s;
    cin>>s;
    for(int i=0;i<s.size()-1;i++)
    {
        if(s[i]<='9'&&s[i]>='0')
        {
            int t=0;
            while(s[i]<='9'&&s[i]>='0')
            {
                t=t*10+s[i]-'0';
                i++;
            }
            stk.push(t);
        }
        if(s[i]!='.')
        {
            stk.push(cal(s[i]));
        }
    }
    cout<<stk.top()<<endl;
    return 0;
}