文章目录
- 一:基本概念
- 1.1 介绍
- 1.2 原理
- 1.3 插入排序法思想
- 二:代码实现
- 2.1 源码
- 2.2 执行结果
- 2.3 测试八万条数据
- 三:算法分析
- 3.1 时间复杂度
- 3.2 空间复杂度
- 3.3 稳定性
一:基本概念
1.1 介绍
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
1.2 原理
一般也被称为 直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排席方法,它的基本思想是
将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。在其实现过程使用双层循环,外层循环对除
了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
1.3 插入排序法思想
插入排序(InsertionSorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
- 将待排序序列分为两部分,一部分有序一部分无序。
- 我们把第一个元素看作有序序列,从第二个元素到最后为无序序列。
- 将无序序列中每一个元素依次插入到有序序列的合适位置–从小到大(从大到小)。

二:代码实现
2.1 源码
/**
* 插入排序
*
* @author ikun
*/
public class InsertSort {
public static void main(String[] args) {
int[] array = new int[5];
for (int i = 0; i < array.length; i++) {
//Math.random() * 80000生成0到100的随机数
array[i] = (int) (Math.random() * 80);
}
System.out.println("排序前:" + Arrays.toString(array));
insertSort(array);
}
/**
* 插入排序
*
* @param array 需要排序的数组
*/
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
//使用逐步推倒的方式来讲解,便于理解
//第一轮 {101, 34, 119, 1} -> { 34,101,119,1}
//定义待插入的数据
//第一轮的话,待插入的数就是array[1]
int insertVal = array[i];
//定义待插入数据的下标,即array[1]的前一个下标
//int insertIndex = 1 - 1;
int insertIndex = i - 1;
//给insertVal找到一个插入的位置
//说明
//1.insertIndex >= 0是保证再给insertIndex找插入位置时,不会数组下标越界
//2.insertVal < array[insertIndex]说明待插入的数,还没找到插入的位置
//3.此时需要将array[insertIndex],也就是101后移
while (insertIndex >= 0 && insertVal < array[insertIndex]) {
//将array[insertIndex]后移
array[insertIndex + 1] = array[insertIndex];
//因为要和前面每一个数据进行比较,所以要将要插入的位置减一,挨个比较
insertIndex--;
}
//当退出while循环时,说明插入的位置找到,则insertIndex + 1
array[insertIndex + 1] = insertVal;
System.out.println("第" + i + "轮插入后:" + Arrays.toString(array));
}
}
}
2.2 执行结果
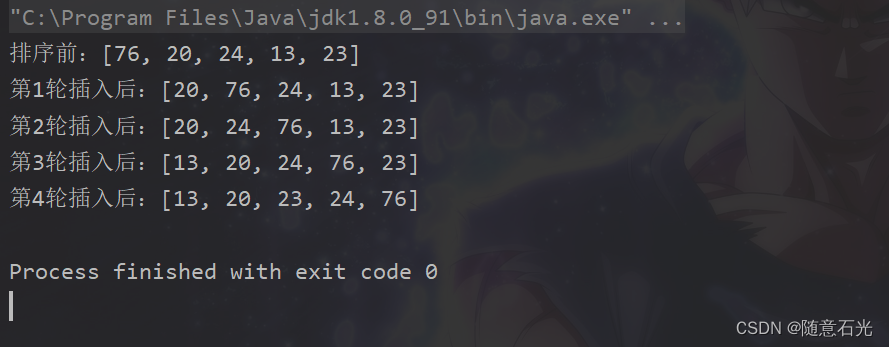
2.3 测试八万条数据
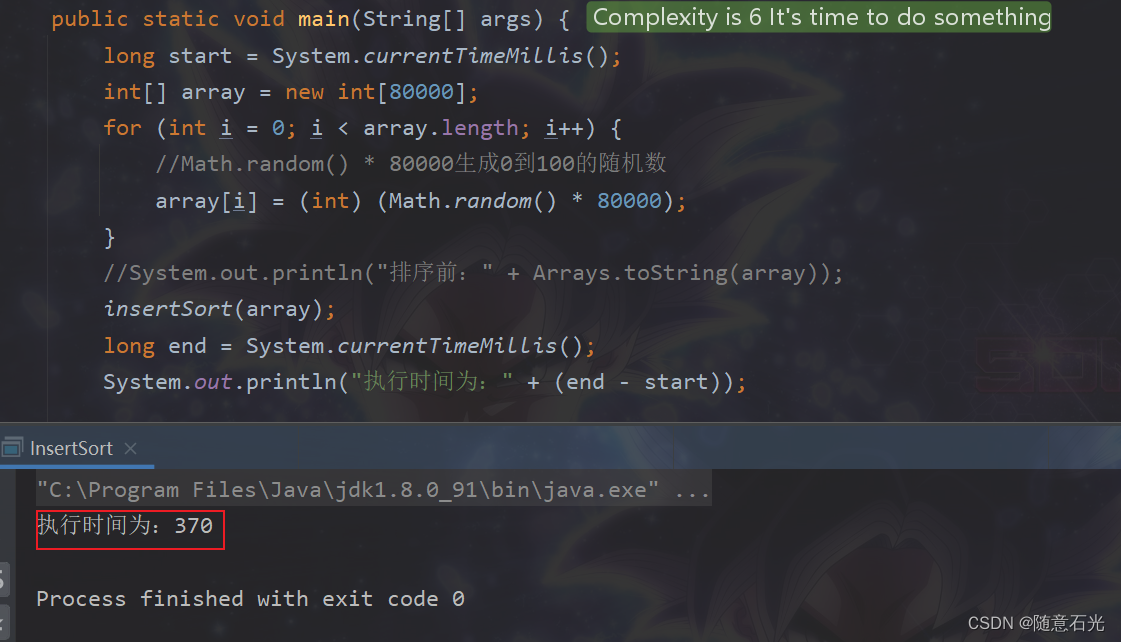
可以看出执行的时间只有370ms,是低于冒泡排序和选择排序的
三:算法分析
3.1 时间复杂度
O(n2)
3.2 空间复杂度
O(1)
3.3 稳定性
稳定的排序算法,其稳定性在于相同值的元素进行插入排序完成后相对位置不发生改变。