一、分治法的定义

分而治之可称为分治法，即逐个击破，分而治之，含义是将一个复杂问题分解成多个子问题来解决，一直分下去直到每个子问题都可以简单地求解出来，最后合并所有的解，从而得到复杂问题的解。该方法在《数据结构》中的应用场景有查找算法（二分查找）、排序算法（快速排序、归并排序）等等。

一个问题可以采用分治法的特征有以下：
①问题可分解为很多小规模的相同子问题；【前提】
②分解后的子问题后可以很容易地解决；
③各个子问题是相互独立的；【效率】
④分解的子问题的解最后可以合并。【关键】

二、分治法的基本步骤

• 分治法主要分为分解、治理两大步骤，分解，是将问题分解成多个规模上较小、内容上相互独立、性质上与原问题相同的子问题；治理，是对各个子问题直接求解，若仍不容易解决，则再进行进一步分解后再求解，由于性质相同，所以求解子问题的解决方法和原问题是相同的；治理中包含合并，是将得到的各个子问题的解进行合并，从而得到原问题的解。

三、分治法的应用

（一）查找算法

二分（折半）查找

• 二分查找中运用到了分治法，它属于一种线性查找，只适用于有序的顺序表，首先，将有序序列分为两部分，每次取中间元素与查找元素进行比较，若为中间元素则停止查找，此时查找成功；若小于中间元素则沿序列左半部分继续缩小范围进行查找【左半部分分解和治理】，若大于中间元素则沿序列右半部分继续缩小范围进行查找【右半部分分解和治理】，一直缩小直到查找到该元素为止，此时查找成功，否则，查找失败。

其基本步骤如下：
（1）通过一个一维数组s[n]来存放具有n个元素的有序顺序表，设查找元素为x；
（2）初始化查找范围，令变量low=0，high=n-1，分别指向数组的头和尾；
（3）取中间元素，即变量mid=⌊(low+high)/2⌋（向下取整，取比它小的最大整数）；
（4）将指定查找的元素x与中间元素进行比较，若相等，则查找成功，查找的元素即为mid指向的位置；若不相等，根据大小关系，选择中间元素的另一边元素继续进行比较：
①若查找关键字小于中间元素，左半部分分解和治理，low不变，high=mid-1；
②若查找关键字大于中间元素，右半部分分解和治理，high不变，low=mid+1。
（5）重复以上(3)、(4)步骤，直到查找成功或查找范围超出（low>high）为止结束算法。

通过二分查找算法在有序序列{-7，-2，0，1，3，4，5，9}中查找元素6。

假定该有序序列存放在一个一维数组s[8]中，长度为8，如下：

下标	0	1	2	3	4	5	6	7
元素	-7	-2	0	1	3	4	5	9

首先，令low=0，high=7，即mid=⌊(low+high)/2⌋=⌊7/2⌋=⌊3.5⌋=3，将序列一分为二：

由于x=6大于mid=3的元素1，即6>1，此时向右半部分分解和治理，即x可能位于序列s[mid+1，high]范围内，即s[4，7]中。此时high=7不变，low=mid+1=4，mid=⌊(low+high)/2⌋=⌊11/2⌋=⌊5.5⌋=5，将序列一分为二：

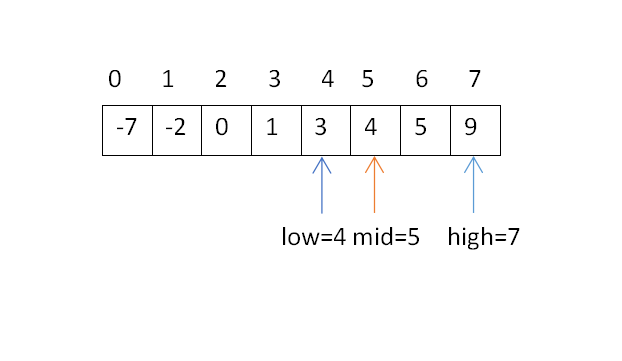
由于x=6大于mid=5的元素4，即6>4，继续向右半部分分解和治理，即x可能位于序列s[mid+1，high]范围内，即s[6，7]中。此时high=7不变，low=mid+1=6，mid=⌊(low+high)/2⌋=⌊13/2⌋=⌊6.5⌋=6，将序列一分为二：

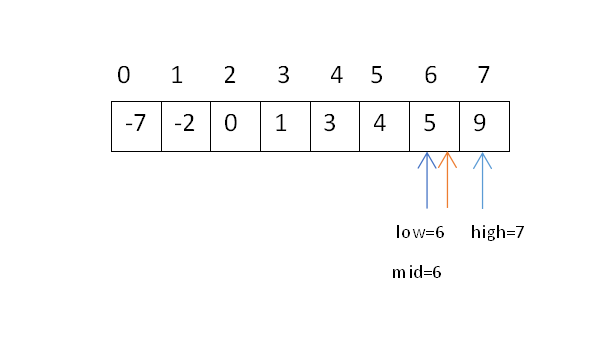
由于x=6大于mid=6的元素5，即6>5，继续向右半部分分解和治理：

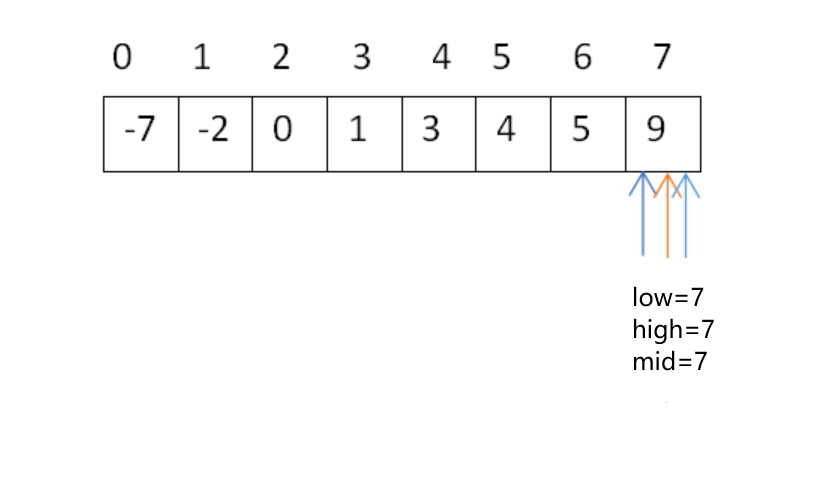
此时仍未找到要查找的元素，所以查找失败，序列中无该元素。

• 通过以上可以得出，当有序序列为n=1时，查找元素x需要的时间复杂度为T(n)=O(1)；而当n>1时，子问题的规模为n/2，其递归关系式为T(n)=T(n/2^x)+xO(1)，即令n=2^x，则x=log₂n，二分查找的T(n)=O(1)+O(log₂n)，即二分查找的时间复杂度为O(log₂n)。

也可以通过在折半判定树求出时间复杂度，由于比较次数最多不会超过树的高度h=⌈log2(n+1)⌉，即折半查找的时间复杂度为O(log₂n)。

（二）排序算法

在之前的文章，数据结构学习笔记—— 排序算法总结【ヾ(≧▽≦*)o所有的排序算法考点看这一篇你就懂啦！！！】，我们分析过：

• 快速排序、堆排序和归并排序是改进型的排序算法，其平均时间复杂度均为O(nlog₂n)，快速排序和归并排序都采用分治的思想，而堆排序是通过使用堆这种数据结构。

排序算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度
快速排序	O(nlog2n)	O(nlog2n)	O(n2)
堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)
归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)

1、交换排序——快速排序

快速排序基于分治，通过多次划分操作来实现排序思想。每一趟排序中选取一个关键字作为枢轴，枢轴将待排序的序列分为两个子序列，比枢轴小的元素移到其前，比枢轴大的元素移到其后，这是一趟快速排序，然后分别对两个部分按照枢轴划分规则继续进行排序，直至每个区域只有一个元素为止，最后达到整个序列有序。快速排序的代码中有递归的应用，其递归的进行需要栈来辅助，代码如下：

/*快速排序*/
void QuickSort(int r[],int low,int high) {
	int temp,i=low,j=high;
	temp=r[i];	//将其设为枢轴，对序列进行划分
	while(i<j) {
		while(i<j&&r[j]>=temp)	//从右往左寻找，找到小于temp的元素
			j--;
		r[i]=r[j];	//放在枢轴temp的左边
		while(i<j&&r[i]<=temp)	//从左往右寻找，找到大于temp的元素
			i++;
		r[j]=r[i];	//放在枢轴temp的右边
	}
	r[i]=temp;	//一趟快速排序结束，枢轴temp被放到其最终位置
	if(low<i-1)
		QuickSort(r,low,i-1);	//递归，对枢轴temp的左边区域进行快速排序
	if(i+1<high)
		QuickSort(r,i+1,high);	//递归，对枢轴temp的右边区域进行快速排序
}

其基本步骤如下：
（1）分解，首先选择一个枢轴元素temp，枢轴元素的位置大小为low ≤ temp ≤ high，以该元素划分为两个子序列；

由于快速排序每趟只确定枢轴元素的最终位置，所以第n趟快速排序完成时，会有n个以上的元素处于其最终结果位置上，即它们两边的元素分别比它大或小。

（2）治理，对子序列进行治理，然后使两个子序列中的所有元素小于等于和大于等于枢轴元素，即[low，temp-1] ≤ temp和[temp+1，high] ≥ temp：
①求解子问题，对枢轴元素两边的子序列[low，temp-1]（枢轴temp的左边区域）、[temp+1，high]（枢轴temp的右边区域）分别递归调用快速排序函数QuickSort(r,low,i-1)、QuickSort(r,i+1,high)继续进行快速排序；
②合并子问题，当两个子序列都有序时，由于是基于枢轴元素排序的，所以整体序列也呈有序。

设一组初始记录关键字序列{5，8，6，3，2}，以第一个记录关键字5为基准进行一趟从大到小快速排序。

以第一个元素5为枢轴，原位置空出，i和j指向序列的头、尾元素，开始进行第一趟快速排序：

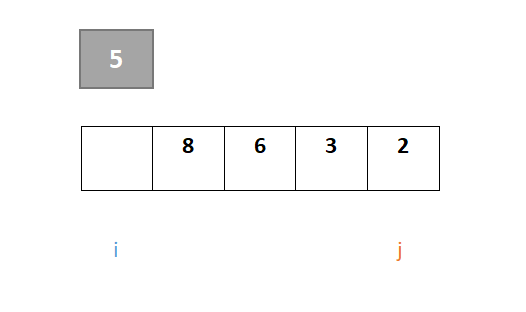
整个过程保证i指针左边是比枢轴元素小的元素，j指针右边是比枢轴元素大的元素（j指针找小于，i指针找大于）。首先对于j，从右往左一直寻找，找到小于枢轴元素的元素，若找到则j停下，由于元素2大于枢轴元素5，此时j的值与i的值交换：


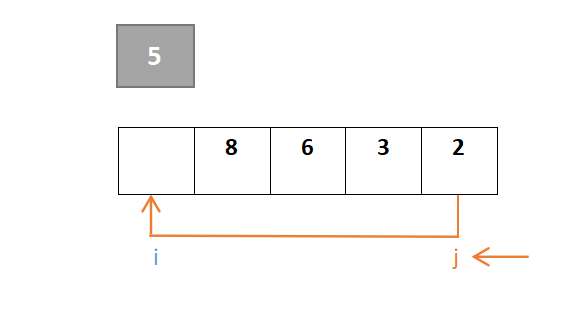
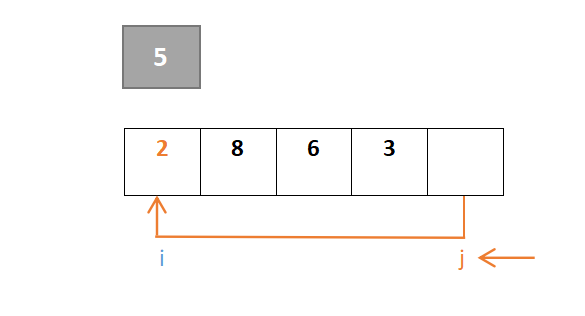
然后对于i，从左往右一直寻找，找到大于枢轴元素的元素，若找到则i停下，由于元素2小于则继续向右，到元素8停下，8>5：


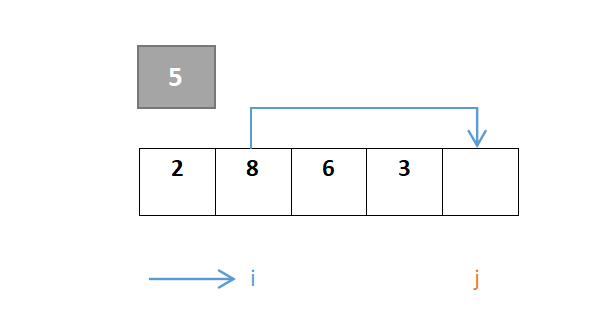
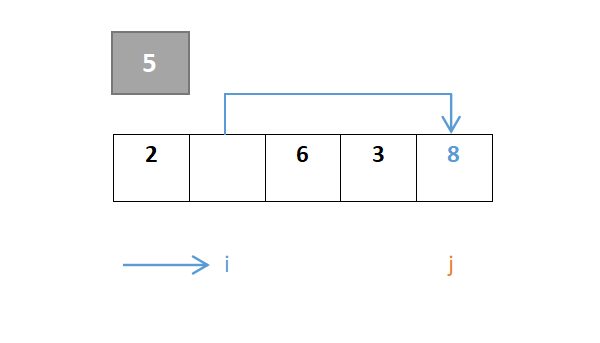
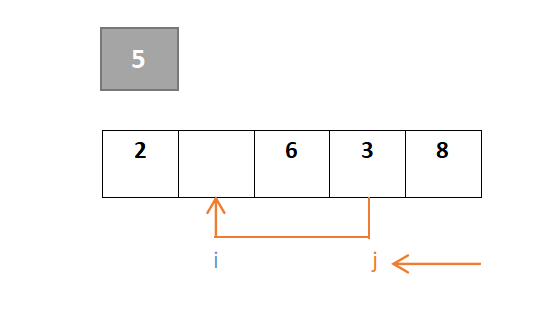
j继续移动，由于元素8大于则继续向左，到元素3停下，3<5，此时j与i交换：


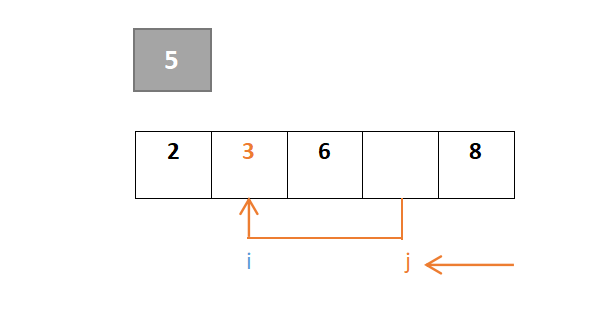
…………重复步骤：


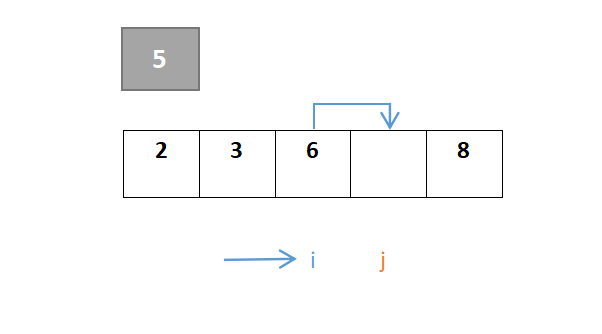
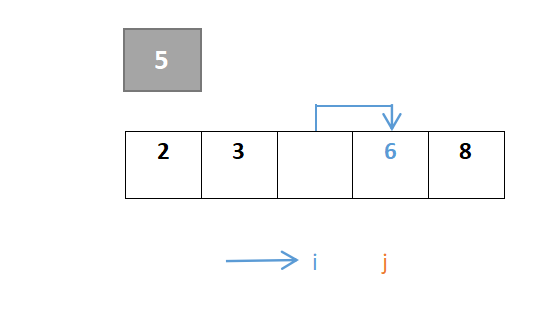
j继续移动，此时i与j相遇，最终位置即是枢轴元素的位置：

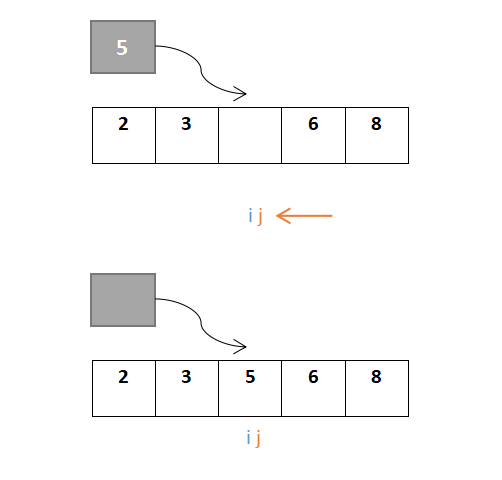
故快速排序的结果为{2，3，5，6，8}。

可以从划分操作和原序列排列上进行分析其时间复杂度：

• 当快速排序的初始序列为有序或逆序时（或划分取的枢轴元素为当前序列最大或最小元素），为最坏情况，当n=1时为T(n)=O(1)，而n>1时，递归函数为T(n)=T(n-1)+O(n)=O[n(n+1)/2]=O(n²)，即最坏时间复杂度会达到O(n²)；而初始序列越接近无序或基本上无序时（或划分取的枢轴元素为当前序列中值元素），为最好情况，当n=1时为T(n)=O(1)，而n>1时，递归函数为T(n)=2T(n/2)+O(n)=O(nlog₂n)，即最好时间复杂度为O(nlog₂n)；当平均情况下，其平均时间复杂度也为O(nlog₂n)。

排序算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度
快速排序	O(nlog2n)	O(nlog2n)	O(n2)

• 快速排序中需借助栈来进行递归，其空间复杂度与递归层数（栈的深度）有关，最坏情况下二叉树为最大高度，为n层，即最大递归深度，所需要的栈的空间为n，即最坏空间复杂度为O(n)；而最好情况下为二叉树的最小高度⌊
  log₂n ⌋，即最小递归深度，此时需要的栈的空间为⌊
  log₂n ⌋，即最好空间复杂度为O(log₂n)；平均情况下，所需要的栈的空间为log₂n，即平均空间复杂度为O(log₂n)。

2、归并排序

归并排序是将两个或两个以上的有序表组合成一个新的有序表，它也采用的是分治思想，例如将两个有序表合并成一个有序表。另外，对于N个元素进行k路归并排序，其排序的趟数m满足k^m=N，即m=⌈log_kN⌉（⌈⌉表示向上取整，取比自己大的最小整数）。

归并排序也是一个递归的过程，分别对划分后的左右子序列进行处理，Merge()函数中借助到了一个辅助数组r1，首先将划分的子序列放在该数组相邻位置，每次从该数组的两段子序列中取出元素进行比较，较小者放回原本的数组r[]中，代码如下，：

/*归并*/
void Merge(int r[],int low,int mid,int high) {
	int *r1=(int *)malloc((high-low+1)*sizeof(int));	//辅助数组r1 
	for(int k=low; k<=high; k++)
		r1[k]=r[k];	//将r中的所有元素复制到r1中 
	for(i=low,j=mid+1,k=i; i<mid&&j<=high; k++) {//low指向为第一个有序表的第一个元素，j指向第二个有序表的第一个元素
		if(r1[i]<=r1[j])	//比较r1的左右两段中的元素 
			r[k]=r1[i++];	//将较小值复制到r1中 
		else
			r[k]=r[j++];
	}
	while(i<=mid)
		r[k++]=r1[i++];	//若第一个表没有归并完的部分复制到尾部 
	while(i<=high)
		r[k++]=r1[j++];	//若第二个表没有归并完的部分复制到尾部 
}

/*归并排序*/
void MergeSort(int r[],int low,int high) {
	if(low<high) {
		int mid=(low+high)/2;	//划分 
		MergeSort(r,low,mid);	//对左有序子表递归 
		MergeSort(r,mid+1,high);	//对右有序子表递归 
		Merge(r,low,mid,high);	//归并
	}
}

以二路归并排序为例，其基本步骤如下：
（1）分解，将序列分为两个大致相同的子序列；

（2）治理，对子序列进行治理：
①求解子问题，将两个子序列递归进行排序；
②合并子问题，将已经呈有序的两个子序列进行合并，从而整体序列也呈有序。

例如，对于序列{34，15，13，93，65，74，20，17}，对其进行归并排序，基本过程如下：

将初始序列分为8个只含有1个元素的子序列：

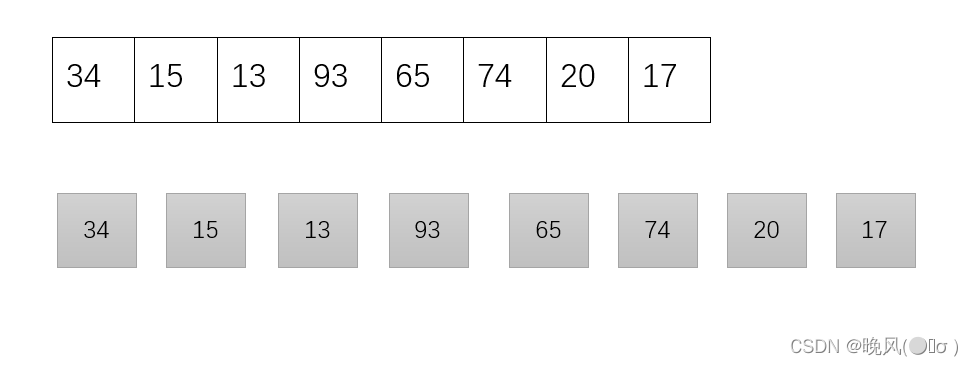
第一趟归并，两两归并，形成若干个由两个元素组成的子序列：

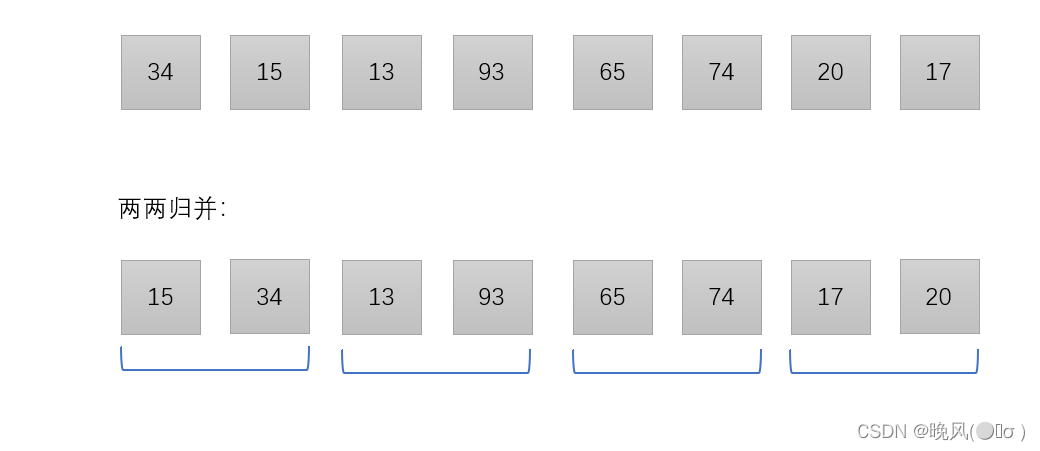
第二趟归并，继续两两归并，形成两个由四个元素组成的子序列：

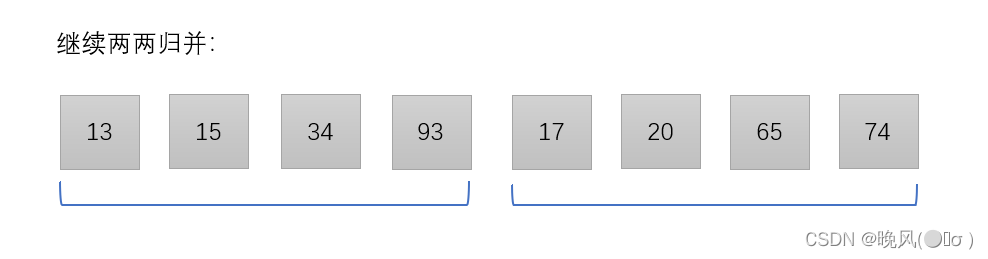
第三趟归并，继续两两归并，即可形成一个完整的有序序列：

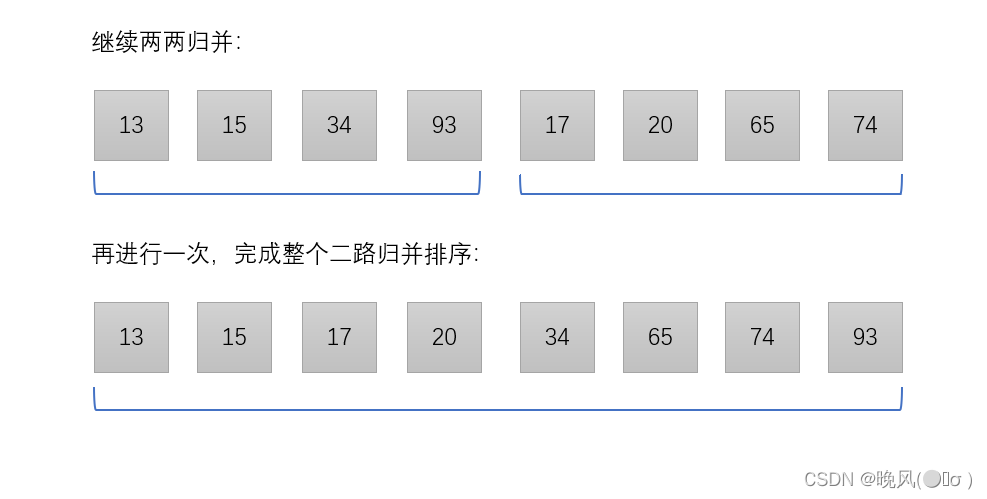
最终序列为{13、15、17、20、34、65、74、93}。

• 归并排序中，比较次数与初始序列无关，即分割子序列与初始序列是无关的，所以其时间复杂度没有最坏和最好情况。当有序序列为n=1时，需要的时间复杂度为T(n)=O(1)；而当n>1时，分割的子序列所需规模为2T(n/2)，Merge()函数的时间为O(n)进行比较和复制，所以递归关系式为T(n)=2^xT(n/2^x)+xO(n)，即令n=2^x，则x=log₂n，归并排序的T(n)=nO(1)+log₂n，即归并排序的时间复杂度为O(nlog₂n)。

排序算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度
归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)

• 由于归并排序中也用到了栈，其递归工作栈的空间复杂度为O(log₂n)，由于另外还需用到辅助数组，其空间复杂度为O(n)，所以该排序算法的空间复杂度为O(n)。