http://cplusoj.com/d/senior/p/SS231007C

考虑枚举gcd，然后容斥，恰好转至少。$g$ 表示gcd恰好为 $d$，$f$ 表示至少为 $d$

显然有 $f(d)={\sum }_{d|n}g(n)$，可以直接莫反成：$g(d)={\sum }_{d|n}f(n{)}^{\mu (\frac{n}{d})}$，但其实不用这么麻烦。从大往小处理 $d$，则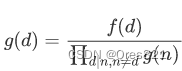

考虑如何计算 $f$，直接上拆贡献。枚举每个质因子。对于 $d$ 我们可以直接计算。对于 $p^c$ 的东西，我们要保证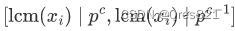

直接算很麻烦。考虑容，然后发现不用容，直接恰好转至少后变差分就行了。

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 2000010
//#define M
#define mo 998244353
int pw(int a, int b) {
	int ans=1; 
	while(b) {
		if(b&1) ans*=a; 
		a*=a; b>>=1; 
		ans%=mo; a%=mo; 
	}
	return ans; 
}
int pw(int a, int b, int p) {
	int ans=1; 
	while(b) {
		if(b&1) ans*=a; 
		a*=a; b>>=1; 
		ans%=p; a%=p; 
	}
	return ans; 
}
int fac[N], inv[N], ifac[N]; 
void init(int n) {
	int i; 
	for(i=fac[0]=1; i<=n; ++i) fac[i]=fac[i-1]*i%mo; 
	ifac[n]=pw(fac[n], mo-2); 
	for(i=n-1; i>=0; --i) ifac[i]=ifac[i+1]*(i+1)%mo; 
    for(i=1; i<=n; ++i) inv[i]=ifac[i]*fac[i-1]%mo; 
}
int C(int n, int m) {
	if(m>n) return 0;
	return fac[n]*ifac[m]%mo*ifac[n-m]%mo; 
}
void Add(int &a, int b) {
	a+=b; if(a>=mo || a<=-mo) a%=mo; 
    if(a<0) a+=mo; 
}
void Mul(int &a, int b) {
	a*=b; if(a>=mo || a<=-mo) a%=mo; 
    if(a<0) a+=mo; 
}
void Mod(int &a) {
	if(a>=mo || a<=-mo) a%=mo; 
    if(a<0) a+=mo; 
}
void Mod(int &a, int p) {
	if(a>=p || a<=-p) a%=p; 
    if(a<0) a+=p; 
}
void Add(int &a, int b, int p) {
	a+=b; if(a>=p || a<=-p) a%=p; 
    if(a<0) a+=p; 
}
const int iv2=pw(2, mo-2); 
int b[N]; 
vector<int>z; 
void prim(int n) {
	memset(b, -1, sizeof(b)); b[1]=0;  
	for(int i=2; i<=n; ++i) {
		if(b[i]) z.pb(i); 
		for(int j : z) {
			if(i*j>n) break; 
			b[j*i]=0; if(i%j==0) break; 
		}
	}
}
int n, m, i, j, k, T;
int ans, lim, lstlim, d, D, g[N], f[N], c, p, P; 
int S[N], s[N]; 

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
		freopen("number.in", "r", stdin);
	freopen("number.out", "w", stdout);
//	T=read();
//	while(T--) {
//
//	}
	n=read(); m=read(); init(2000000); 
	prim(2000000); 
	lstlim=0; ans=1; 
	for(d=m; d>=1; --d) {
		lim=m/d; 
//		if(lim==lstlim) {
//			f[d]=f[d+1]; g[d]=g[d+1];
//		}
//		else {
			f[d]=pw(d, pw(lim, n, mo-1)); 
			for(auto p : z) {
				if(p>lim) break; 
//				printf("%lld : \n", p); 
				for(c=0, P=1; P<=lim; P*=p, ++c) {
					S[c]=pw(lim-lim/(P*p), n, mo-1); 
//					printf("S %lld : %lld %lld\n", c, S[c], lim-lim/(P+1)); 
				}
				for(c=1, P=p; P<=lim; P*=p, ++c) {
					s[c]=S[c]-S[c-1]; Mod(s[c], mo-1); 
//					printf("s %lld : %lld\n", c, s[c]); 

					Mul(f[d], pw(P, s[c])); 
//					printf("%lld\n", f[d]); 
				}
			}
			g[d]=f[d]; 
			for(D=2*d; D<=m; D+=d) Mul(g[d], pw(g[D], mo-2)); 
//		}
//		lstlim=lim; 
//		printf("%lld : %lld %lld %lld\n", d, f[d], g[d], pw(g[d], d)); 
		Mul(ans, pw(g[d], d)); 
	}
	Mod(ans); 
	printf("%lld", ans); 
	return 0;
}