一、题目描述与要求

二叉树中和为某一值的路径(二)_牛客题霸_牛客网 (nowcoder.com)

题目描述

输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。

1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点

2.叶子节点是指没有子节点的节点

3.路径只能从父节点到子节点，不能从子节点到父节点

4.总节点数目为n

如二叉树root为{10,5,12,4,7},expectNumber为22

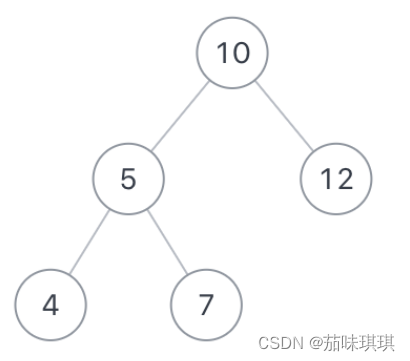
则合法路径有[[10,5,7],[10,12]]

数据范围:

树中节点总数在范围 [0, 5000] 内

-1000 <= 节点值 <= 1000

-1000 <= expectNumber <= 1000

示例

示例1：

输入：{10,5,12,4,7},22

返回值：[[10,5,7],[10,12]]

说明：返回[[10,12],[10,5,7]]也是对的

示例2：

输入：{10,5,12,4,7},15

返回值：[]

示例3：

输入：{2,3},0

返回值：[]

示例4：

输入：{1,3,4},7

返回值：[]

---

二、解题思路

根据题目描述，我们需要找到二叉树中结点值的和为target的所有路径。

路径定义为从树的根结点开始往下一直到叶子结点所经过的结点，因而我们需要从根结点开始遍历所有结点一直到叶子结点的所有路径，并且判断其是否满足target，而我们怎么去实现遍历完一条分支之后转移到另一条分支呢？那就是回溯，也就是当我们访问完当前这一条路径并且到达叶子结点的时候，我们返回上一个结点，去访问另一个分支，这样就能够找出所有的路径。

这一思路也就是遍历图的深度优先算法思想。

首先我们定义两个vector，一个用来存储符合题目要求的所有路径，另一个用来存储目前所走的路径，需要设置为全局变量，因为dfs函数时另外写的，方便访问，而不用通过传参；

然后我们调用dfs函数来寻找路径。

首先先判断是否为空树/空节点，是的话就返回空/返回上一级；

然后就是将当前结点存入path中，这里用emplace_back/push_back都可以，emplace_back的效率会更高一点；

然后更新目前的目标值，也就是减去当前结点的值；

然后判断当前结点是否为叶子结点，如果是的话判断此时的target是否等于0，如果以上条件都满足的话就说明当前路径是满足条件的路径，将路径存入v中，否则则对当前结点的左右子树继续进行遍历；

每遍历完一条分支之后，都需要回溯到上一个结点，从而去访问另一条分支，因而需要将当前结点弹出；

最后返回v即可。

---

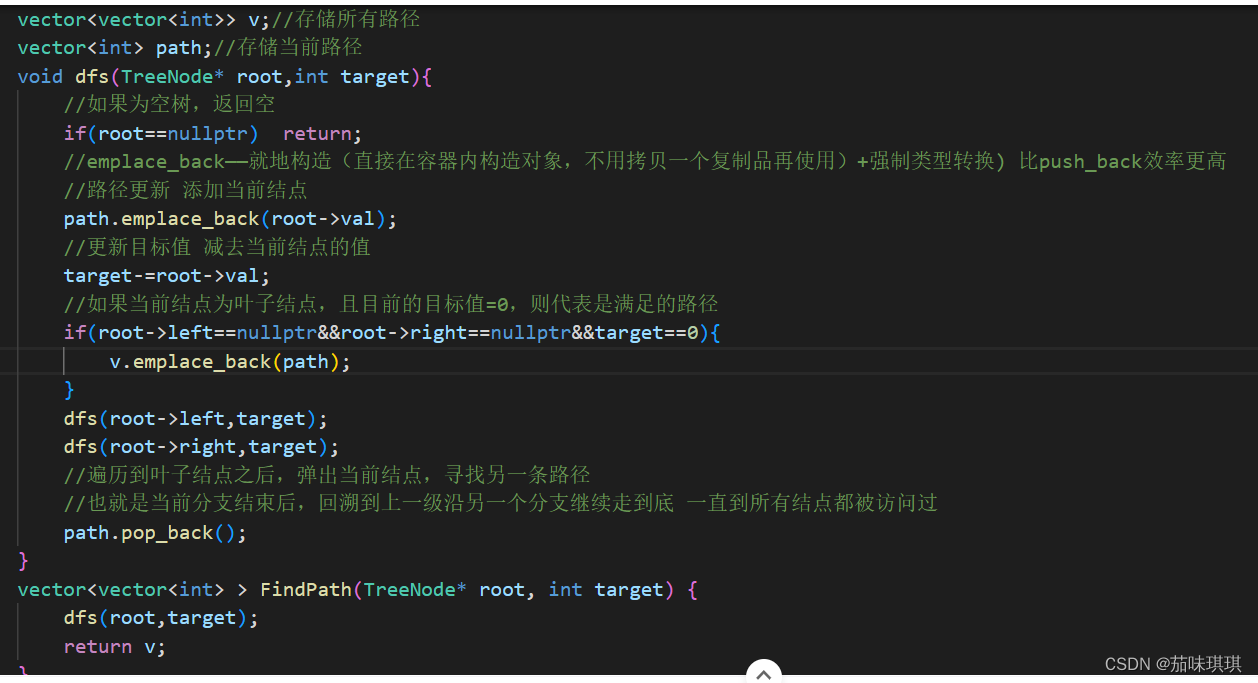
三、具体代码

#include <vector>
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @param target int整型 
     * @return int整型vector<vector<>>
     */
    vector<vector<int>> v;//存储所有路径
    vector<int> path;//存储当前路径
    void dfs(TreeNode* root,int target){
        //如果为空树，返回空
        if(root==nullptr)  return;
        //emplace_back——就地构造（直接在容器内构造对象，不用拷贝一个复制品再使用）+强制类型转换) 比push_back效率更高
        //路径更新 添加当前结点
        path.emplace_back(root->val);
        //更新目标值 减去当前结点的值
        target-=root->val;
        //如果当前结点为叶子结点，且目前的目标值=0，则代表是满足的路径
        if(root->left==nullptr&&root->right==nullptr&&target==0){
            v.emplace_back(path);
        }
        dfs(root->left,target);
        dfs(root->right,target);
        //遍历到叶子结点之后，弹出当前结点，寻找另一条路径
        //也就是当前分支结束后，回溯到上一级沿另一个分支继续走到底 一直到所有结点都被访问过
        path.pop_back();
    }
    vector<vector<int> > FindPath(TreeNode* root, int target) {
        dfs(root,target);
        return v;
    }
};