单源最短路径

🚀最短路径：从图G的某个顶点出发到达另一个顶点的最短路径，其中最短是指路径上边的权值和最小。
🚀单源最短路径：从图G中的某一顶点出发到达其余顶点的最短路径。

Dijkstra

算法原理

🚀针对一个带权有向图，将所有的顶点划分为两个集合S和Q，S是已经确定最短路径的顶点结合，Q是还未确定最短路径的顶点集合。每次从Q中找出一个从起点s到达该结点代价最小(权值和最小)的结点u(可见迪杰斯特拉算法同样采取的是贪心策略)，将u从集合Q中移除，并放入S中，对u所邻接的顶点做一次松弛操作。松弛操作即对结点u的邻接点v，判断从起点s到u的代价+u到v的代价是否小于s到v的代价，若小于那么对s到v的代价替换为s到u的代价+u到v的代价。这样依次从Q中选出结点u，直到Q为空为止。

算法特点：比较与其他最短路径的算法，迪杰斯特拉算法的效率较优。但是，此算法只能用于没有负权值的图。

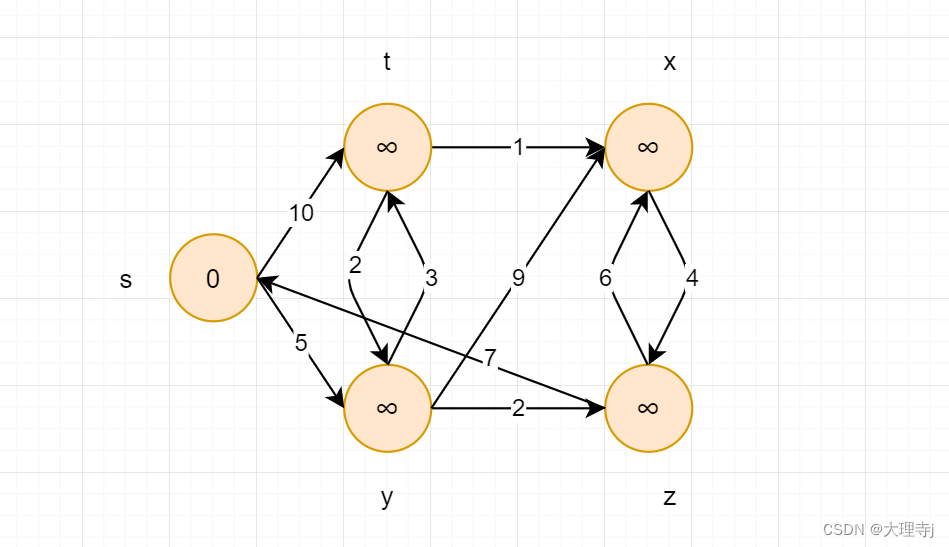
源点为s，即求s到达其他顶点的最短路径。在初始时，s到达其他边的路径长度均为无穷大 ，到达自身的距离为0。

算法执行过程：

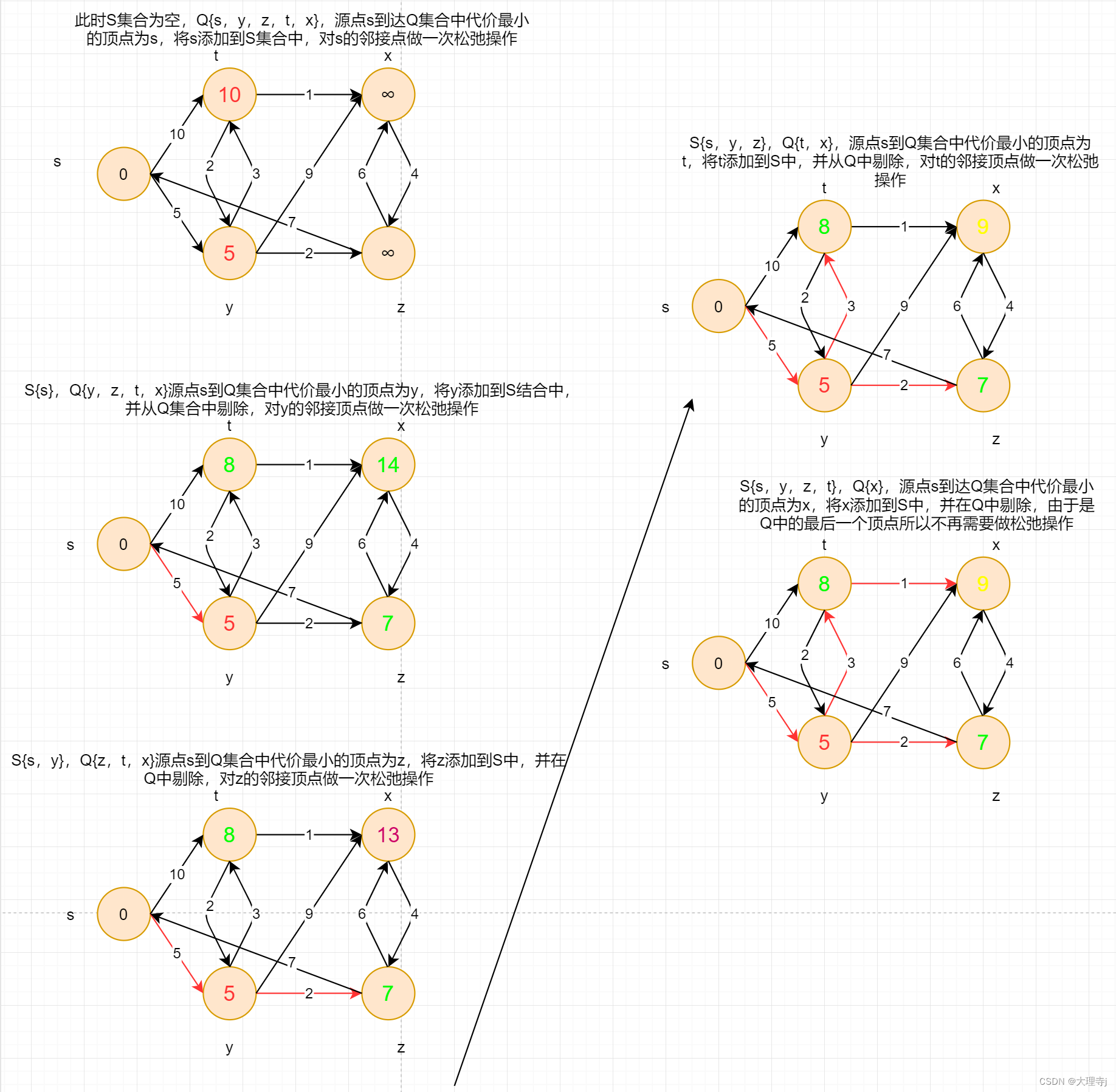
代码实现

void Dijkstra(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {
	//初始化工作
	size_t n = _vertex.size();
	size_t srci = this->GetVertexIndex(src);
	dist.resize(n, W_MAX);
	dist[srci] = 0;
	parent_path.resize(n, -1);
	std::vector<bool> S(n, false); //已选出的顶点集合S
	for (size_t i = 0; i < n; i++) {
		//从dist中选出最短的一条边，S->u
		size_t u = -1;
		W min_eg = W_MAX;
		for (size_t j = 0; j < n; j++) {
			if (dist[j] < min_eg && false == S[j]) {
				u = j;
				min_eg = dist[j];
			}
		}
		//将这个顶点添加到S集合中
		S[u] = true;
		//更新从起始点srci能够到达的其他点的最短路径dist数组
		for (size_t i = 0; i < n; i++) {
			if (_matrix[u][i] != W_MAX && false == S[i] && dist[u] + _matrix[u][i] < dist[i]) {
				dist[i] = dist[u] + _matrix[u][i];
				parent_path[i] = u;
			}
		}
	}
}

dist数组和parent_path数组解释：将源点s到达其他顶点的最短路径数值存储在dist数组中，dist[i]即为源点s到达i号顶点的最短距离。parent_path数组用来记录源点s到达其他顶点的最短路径，采用的是双亲表示法，即该结点存储的内容为源点s到达这个结点路径上的上一个结点的下标。

🚀上面例子中最终两个数值的内容如下：

Bellman-Ford

算法原理

🚀迪杰斯特拉算法不能解决带负权值路径的情况，贝尔曼算法可以解决这一问题。相比于迪杰斯特拉的贪心策略，贝尔曼算法是一种较为暴力的解法，即对每一个结点都做一次松弛操作，但是一轮松弛操作往往不能得到最终结果，存在最短路径于最短路径权值和对应不上的情况，所以要经过多轮更新才能得到最终结果。最多轮次为n-1轮(n:顶点个数)，如果说第n轮更新还能有顶点松弛成功说明存在权值和为负数的环路情况，这种情况贝尔曼算法也是解决不了的(权值和为负数的环路意味着每轮更新都能得到一个更小的结果，是无休止的)。

只经过一轮更新不能的到最终结果的例子：

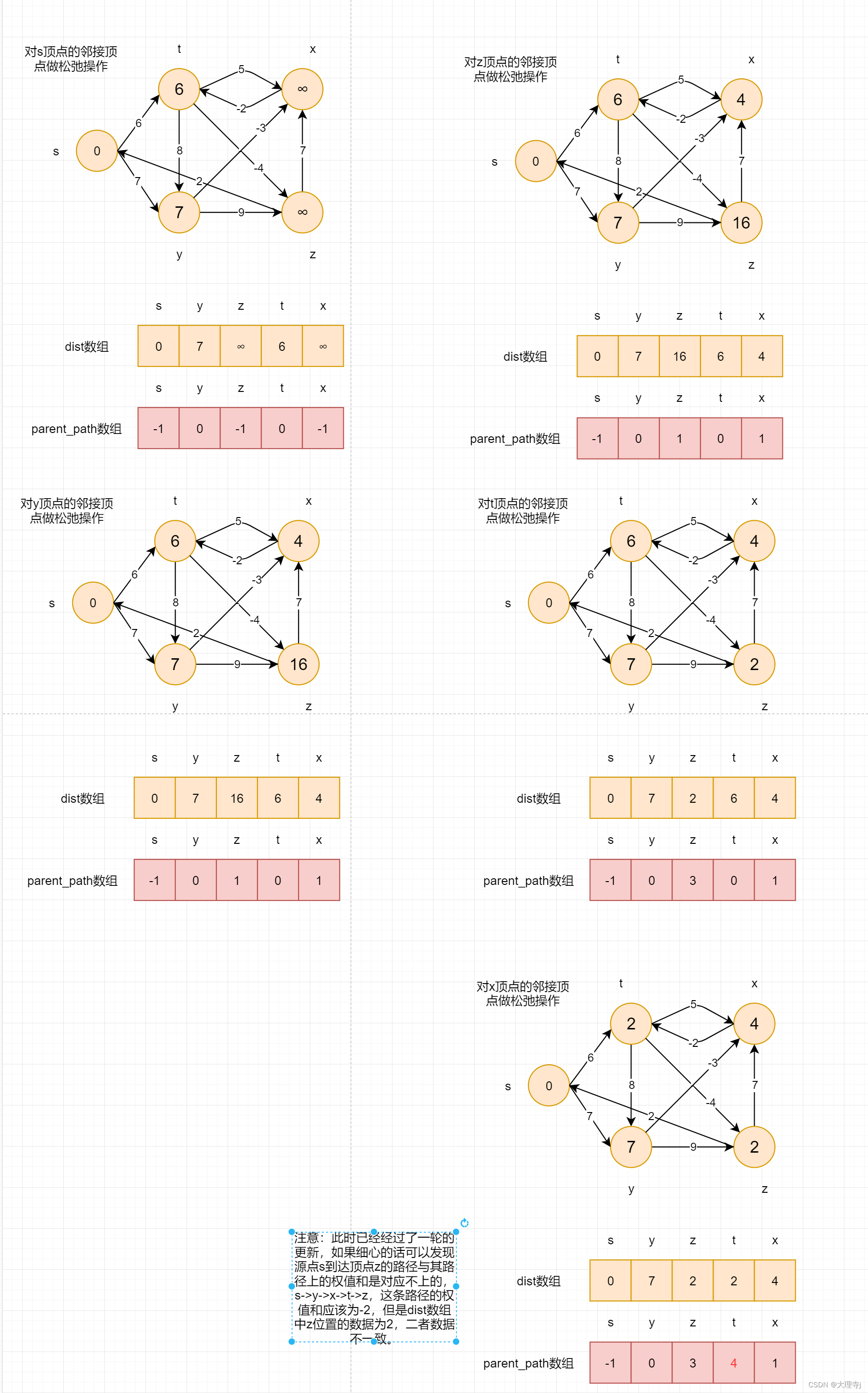
产生上图中这样结果的原因在于更新源点s到达z顶点的最短路径是由对t顶点的邻接顶点做松弛操作得到的，但是在更新源点s到达z的最短路径之后，在对x的邻接顶点做松弛操作的时候，又重新修改了源点s到达t顶点的最短路径，此时在parent_path数组中t位置的数据修改成了x的下标，同样也因此导致了s到达z顶点的路径于路径上的权值和不一致的情况。所以要对t的邻接顶点重新做一次松弛操作，上面这种情况再对t的邻接顶点做一次松弛操作就可以解决问题，但是对于其他更为复杂的问题可能仍旧需要新一轮的松弛操作。那么，松弛操作轮数的上限是多少次呢？n - 1次因为源点出发到达另一个顶点的最短路径至多经过n - 1条边，所以至多经过n - 1轮的更新就能得到最终结果，但是如果第n轮时仍旧存在到达某个点的最短路径发生了更新，那么就说明存在权值和为负数的环路问题。

代码实现

bool Bellman(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {
	//初始化结构
	size_t n = _vertex.size();
	size_t srci = this->GetVertexIndex(src);
	dist.resize(n, W_MAX);
	dist[srci] = 0;
	parent_path.resize(n, -1);
	//寻找最短路径
	for (size_t k = 0; k < n - 1; ++k) {
		bool update = false;
		//update小的优化--如果此轮更新中没有任何一条边松弛成功，此时就可以break退出
		std::cout << "第" << k + 1 << "轮更新: \n";
		for (size_t i = 0; i < n; i++) {
			for (size_t j = 0; j < n; j++) {
				if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j]) {
					update = true;
					dist[j] = dist[i] + _matrix[i][j];
					std::cout << i << "->" << j << ":" << dist[j] << std::endl;
					parent_path[j] = i;
				}
			}
		}
		if (false == update) {
			break;
		}
	}
	//如果经过n-1轮还能进行更新说明出现了负权值环路问题
	for (size_t i = 0; i < n; i++) {
		for (size_t j = 0; j < n; j++) {
			if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j]) {
				return false;
			}
		}
	}
	return true;
}

SPFA优化

🚀在上面分析一轮的松弛操作可能不能得到最终结果的问题时，解决方案就是再对t顶点的邻接顶点做一次松弛操作即可，并不用再对其他顶点做一次松弛操作，也就是说如果要在下一轮中再次对某个顶点的邻接顶点做松弛操作，那么这个顶点一定在本轮中得到了最短路径的更新，否则其不会对其他顶点产生影响。

🚀SPFA算法就是对上面代码中写的贝尔曼算法的一个优化，就是说如果要在下一轮中再次对某个顶点的邻接顶点做松弛操作，那么这个顶点一定在本轮中得到了最短路径的更新，所以在第一轮更新中所有顶点都需要更新，把所有的顶点都入队列，在后续的更新中，如果某个顶点在本轮没有被更新那么其也不会对其他顶点产生影响，就不用再次入队列，相反需要再次入队列， 这样循环置队列为空即可。

SPFA代码实现

void BellmanSPFA(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {
	//初始化结构
	size_t n = _vertex.size();
	size_t srci = this->GetVertexIndex(src);
	dist.resize(n, W_MAX);
	dist[srci] = 0;
	parent_path.resize(n, -1);
	std::queue<size_t> q;
	std::vector<bool> flag(n, false);
	q.push(srci);
	flag[srci] = true;
	while (!q.empty()) {
		size_t top = q.front();
		q.pop();
		flag[top] = false;
		for (size_t i = 0; i < n; i++) {
			if (_matrix[top][i] != W_MAX && dist[top] + _matrix[top][i] < dist[i]) {
				dist[i] = dist[top] + _matrix[top][i];
				parent_path[i] = top;
				if (flag[i] == false) {
					q.push(i);
					flag[i] = true;
				}
			}
		}
	}
}

多元最短路径

Floyd-Warshall

算法原理

🚀佛洛依德算法是一个解决多源的最短路径问题的经典算法，它能够计算出每个顶点到达其余顶点的最短路径，对应用场景通常是带负权值的多源最短路径问题。

🚀佛洛依德算法采用的是动态规划的思想，顶点i到达顶点j的最短路径上至少经过了0个其他顶点，至多经过了n - 2个其他顶点，其状态标识可以定义为dp[i][j][m]，标识顶点i到达顶点j的最短路径上经过了k个其余顶点，其余顶点就是除了起始顶点和终止顶点的其他顶点记作k(k有n-2种取值可能)，所以如果i到j的最短路径经过k，那么dp[i][j][m] = dp[i][k][m-1] + dp[k][j][m-1]，如果i到j的最短路径不经过k，dp[i][j][m] = dp[i][j][m-1]，所以最终dp[i][j][m] = min(dp[i][j][m-1],dp[i][k][m-1]+dp[k][j][m-1])。在正常写代码时通常将其优化为二维的动态规划，因为第三维的m总是依赖于m-1的。

代码实现

void Floyd(std::vector<std::vector<W>>& dist, std::vector<std::vector<int>>& parent_path) {
	//初始化结构
	size_t n = _vertex.size();
	dist.resize(n);
	parent_path.resize(n);
	for (size_t i = 0; i < n; ++i) {
		dist[i].resize(n, W_MAX);
		parent_path[i].resize(n, -1);
	}
	//初始化直接相连的边
	for (size_t i = 0; i < n; i++) {
		for (size_t j = 0; j < n; j++) {
			if (_matrix[i][j] != W_MAX) {
				dist[i][j] = _matrix[i][j];
				parent_path[i][j] = i;
			}
			if (i == j) {
				dist[i][j] = 0;
			}
		}
	}
	//动态规划
	for (size_t k = 0; k < n; ++k) {
		for (size_t i = 0; i < n; ++i) {
			for (size_t j = 0; j < n; ++j) {
				if (dist[i][k] != W_MAX && dist[k][j] != W_MAX &&
					dist[i][k] + dist[k][j] < dist[i][j]) {
					//更新
					dist[i][j] = dist[i][k] + dist[k][j];
					parent_path[i][j] = parent_path[k][j];
				}
			}
		}
	}
}