Leetcode 1492.n的第k个因子

给你两个正整数 n 和 k 。

如果正整数 i 满足 n % i == 0 ，那么我们就说正整数 i 是整数 n 的因子。

考虑整数 n 的所有因子，将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ，请你返回 -1 。

示例 1：

输入：n = 12, k = 3
输出：3
解释：因子列表包括 [1, 2, 3, 4, 6, 12]，第 3 个因子是 3 。

示例 2：

输入：n = 7, k = 2
输出：7
解释：因子列表包括 [1, 7] ，第 2 个因子是 7 。

示例 3：

输入：n = 4, k = 4
输出：-1
解释：因子列表包括 [1, 2, 4] ，只有 3 个因子，所以我们应该返回 -1 。

提示：

1 <= k <= n <= 1000

进阶：

你可以设计时间复杂度小于 O(n) 的算法来解决此问题吗？

一、信息

1.给我两个整数n和k.

2.因子的定义

3.首先获取所有因子然后升序排列，返回第k个因子如果n小于k返回-1

二、分析

条件1.告诉我函数参数的类型

条件2.告诉我因子的定义

条件3.目的

三、步骤

第一步获取两个整型变量 n和k

第二步我们直接循环遍历用i来模拟除数然后循环取余找到所有的能整除N的i它们其实就是N的因子。问题出现用什么装这些数呢？我们用数组来存就行了方便索引

第三步输入k 判断k的范围然后选择对应的路如果K<=n那么就直接按照数组索引就行了，如果大于返回-1.

步骤图：

四、问题出现

五、实现

错误代码：

C语言：

int kthFactor(int N,int k){
	int i,a[1000],sign=0;
	for(i=0;i<=N;i++){
		if(N%(i+1)==0){
			a[i]=i+1;
			sign++;
		}
	}
	if(k<sign){
		return printf("%d",a[k]);
	}else{
		return -1;
	}
}

错误原因：

我的代码思路是基本正确的，但是有几个问题。

1. 数组`a`应该只存储n的因子。在你的代码中，由于使用`a[i]`来存储因子，这可能导致数组的不连续性，即有的数组位置是空的。

2. 当判断`if(k<sign)`时，应该是`k <= sign`。因为如果`k`正好等于因子的数量，那么仍然有一个有效的答案。

3. 当返回结果时，我使用`printf`，但题目要求的是返回整数值。所以我应该直接返回整数而不是打印它。

下面是修改后的代码：

int kthFactor(int N, int k) {
    int i, a[1000], sign = 0;
    
    for (i = 1; i <= N; i++) { // 从1开始遍历到N
        if (N % i == 0) {
            a[sign] = i;  // 存储因子到数组a中的连续位置
            sign++;
        }
    }
    
    if (k <= sign) {  // k应该小于等于因子的数量
        return a[k - 1];  // 注意，因为数组是从0开始的，所以返回的应该是a[k-1]
    } else {
        return -1;
    }
}

这样，我的函数能够正确返回第k个因子，在因子数量少于k时返回-1。

六、标准答案

大师的答案：

C语言：

#include <stdio.h>

int kthFactor(int n, int k) {
    int count = 0; // 用来记录已经找到的因子的数量
    for (int i = 1; i <= n; i++) {
        if (n % i == 0) { // 判断i是否为n的因子
            count++;
            if (count == k) { // 如果已经找到k个因子，则返回当前的因子
                return i;
            }
        }
    }
    return -1; // 如果遍历完所有数字后还没有找到k个因子，则返回-1
}

int main() {
    printf("%d\n", kthFactor(12, 3));  // 3
    printf("%d\n", kthFactor(7, 2));   // 7
    printf("%d\n", kthFactor(4, 4));   // -1
    return 0;
}

改正后我的答案：

C语言：

int kthFactor(int N, int k) {
    int i, a[1000], sign = 0;
    
    for (i = 1; i <= N; i++) { // 从1开始遍历到N
        if (N % i == 0) {
            a[sign] = i;  // 存储因子到数组a中的连续位置
            sign++;
        }
    }
    
    if (k <= sign) {  // k应该小于等于因子的数量
        return a[k - 1];  // 注意，因为数组是从0开始的，所以返回的应该是a[k-1]
    } else {
        return -1;
    }
}

英雄师傅答案：

C语言版本：

int kthFactor(int n,int k){
	int i;
	int cnt=0;
	for(i=1;i<=n;i++){
		if(n%i==0){
			++cnt;
			if(cnt==k){
				return i;
			}
		}
	}
	return -1;
}

大师的进阶答案：

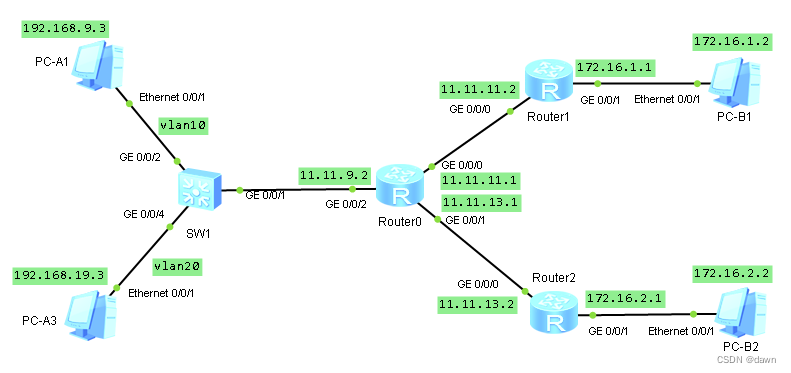
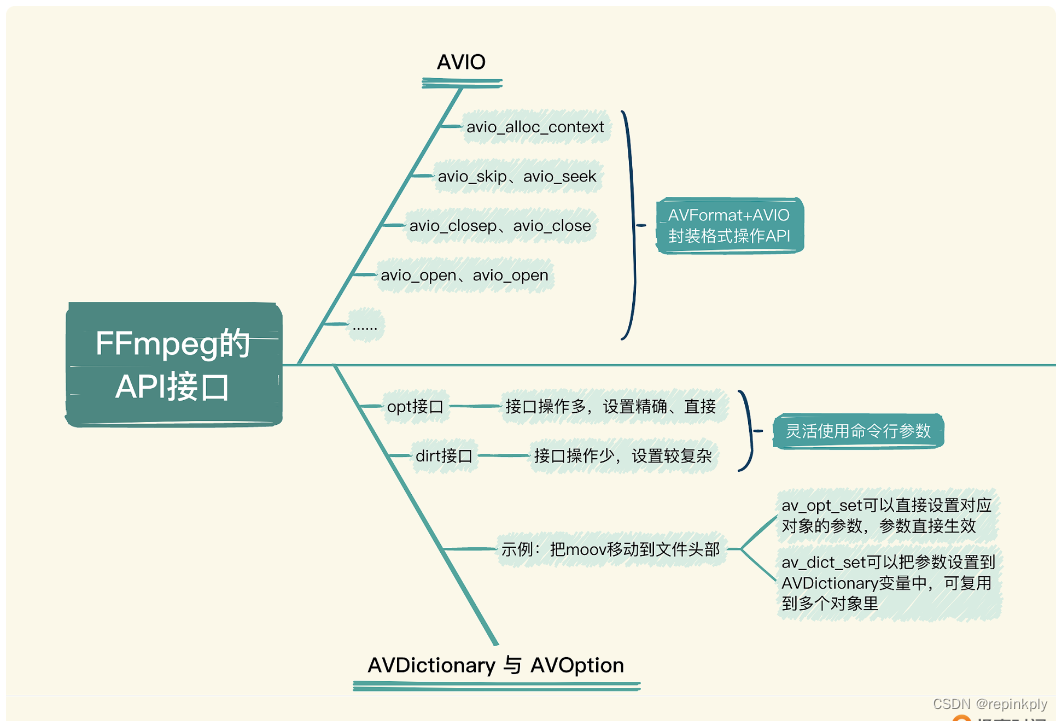
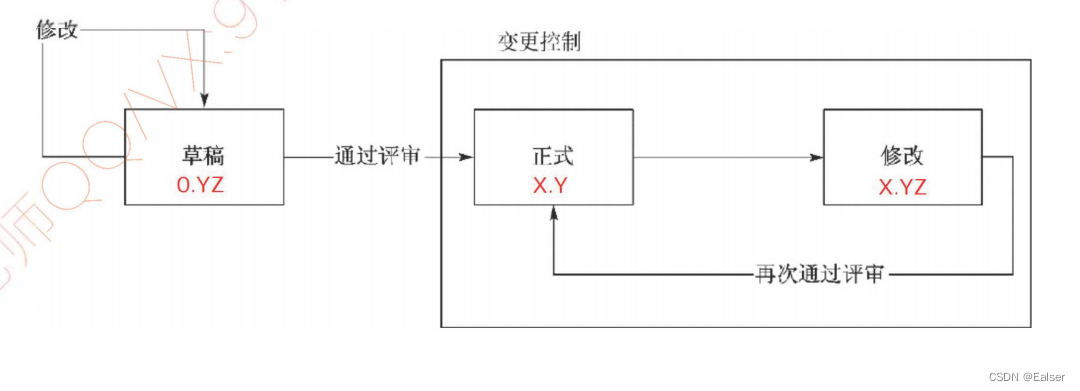
是的，可以设计一个时间复杂度低于 \(O(n)\) 的算法来解决这个问题。一个更高效的方法是只需要遍历到。这是因为n的因子必定是成对出现的（例如，对于n=28，其因子包括1和28、2和14、4和7）。因此，只需遍历到，对于每个找到的因子i，我们可以同时找到另一个因子。

以下是根据这个思路修改的代码：（这个答案是错的正确的在下面）

int kthFactor(int n, int k) {
    int count = 0;

    for (int i = 1; i * i <= n; i++) {
        if (n % i == 0) {
            count++;
            if (count == k) {
                return i;
            }
            
            if (i != n / i) {  // 避免重复计数，例如n=4时，只有一个因子2
                count++;
            }
            if (count == k) {
                return n / i;
            }
        }
    }

    return -1;
}

问题1：不知道你是否会疑问为什么找一个数的因子的时候找到根号下n就可以了，因此我会对这一结论进行证明：

证明问题1：

首先我们要引入一个数学中新的概念——因子配对特性

"因子配对"特性是指当你找到一个数 \(n\) 的因子时，你实际上同时找到了两个因子（除非 \(n\) 是一个完全平方数），这两个因子在乘法上互为倒数。

具体来说，如果 \(a\) 是 \(n\) 的一个因子，并且 \(a \leq \sqrt{n}\)，那么必定存在另一个因子 \(b\)，它是 \(n\) 除以 \(a\) 的结果，即 \(b = \frac{n}{a}\)，并且 \(b \geq \sqrt{n}\)。

这两个因子 \(a\) 和 \(b\) 形成一个配对，因为它们都可以乘以对方得到 \(n\)：\(a \times b = n\)。

举例来说，对于 \(n = 28\):

- \(1\) 是一个因子，它的配对因子是 \(28/1 = 28\)。
- \(2\) 是一个因子，它的配对因子是 \(28/2 = 14\)。
- \(4\) 是一个因子，它的配对因子是 \(28/4 = 7\)。

这里的关键观察是，如果 \(n\) 不是一个完全平方数，那么只有在 \(a = \sqrt{n}\) 时，因子 \(a\) 和 \(b\) 才会相同。在所有其他情况下，因子 \(a\) 和 \(b\) 都会不同。因此，只需要检查到 \(\sqrt{n}\) 就足够了，因为这样可以确保你找到 \(n\) 的所有因子。

好接下来是证明部分：

证明：

要证明为什么找因子只需要检查到 \(\sqrt{n}\)，我们可以从因子的配对特性入手。

**证明**:

1. 假设 \(d\) 是 \(n\) 的一个因子，那么存在整数 \(e\) 使得 \(d \times e = n\)。

2. 假设两者都大于 \(\sqrt{n}\)，即 \(d > \sqrt{n}\) 且 \(e > \sqrt{n}\)。那么它们的乘积 \(d \times e\) 会大于 \(n\)（因为 \(d \times e > \sqrt{n} \times \sqrt{n} = n\)），这与我们的假设 \(d \times e = n\) 矛盾。

3. 同样，如果两者都小于 \(\sqrt{n}\)，那么它们的乘积 \(d \times e\) 会小于 \(n\)。

4. 因此，其中一个因子（如 \(d\)）必然小于或等于 \(\sqrt{n}\)，而另一个因子（如 \(e\)）则必然大于或等于 \(\sqrt{n}\)。

5. 这意味着，为了找到 \(n\) 的所有因子，我们只需要检查小于或等于 \(\sqrt{n}\) 的数。对于每个找到的因子 \(d\)，我们可以得到另一个配对的因子 \(e = n/d\)。

综上所述，为了找到一个数的所有因子，只需要检查到该数的平方根即可。

但是大师这道题目做错了——哈哈哈

正确答案：

#include <math.h> // 为了使用 sqrt 函数

int kthFactor(int n, int k) {
    int count = 0, factor;
    for (factor = 1; factor * factor <= n; ++factor) {
        if (n % factor == 0) {
            ++count;
            if (count == k) {
                return factor;
            }
        }
    }
    --factor;
    if (factor * factor == n) {
        --factor;
    }
    for (; factor > 0; --factor) {
        if (n % factor == 0) {
            ++count;
            if (count == k) {
                return n / factor;
            }
        }
    }
    return -1;
}

有谁知道为什么吗？

问题在于如何处理找到的因子，尤其是当考虑完全平方数时。

在我的最初答案中，我尝试在第一个循环内部直接找到并返回第k个因子。但这种方法在处理大于 \(\sqrt{n}\) 的因子时出现了问题，因为我没有再次从 \(\sqrt{n}\) 开始向下遍历来找到这些因子。

而你提供的答案则修复了这个问题。首先，它遍历到 \(\sqrt{n}\) 来找到小于或等于 \(\sqrt{n}\) 的因子。如果n是完全平方数（例如，n = 36，那么 \(\sqrt{n} = 6\)），它会减少因子值以避免下一个循环中的重复。然后从 \(\sqrt{n}\) 开始向下遍历，这样就可以适当地计数并找到大于 \(\sqrt{n}\) 的因子。

我的错误在于没有正确处理和计数大于 \(\sqrt{n}\) 的因子，这导致了答案的不准确性。

Leetcode官方题解

C++：

class Solution {
public:
    int kthFactor(int n, int k) {
        int count = 0, factor;
        for (factor = 1; factor * factor <= n; ++factor) {
            if (n % factor == 0) {
                ++count;
                if (count == k) {
                    return factor;
                }
            }
        }
        --factor;
        if (factor * factor == n) {
            --factor;
        }
        for (; factor > 0; --factor) {
            if (n % factor == 0) {
                ++count;
                if (count == k) {
                    return n / factor;
                }
            }
        }
        return -1;
    }
};