废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是螺旋矩阵,使用【二维数组】这个基本的数据结构来实现
螺旋矩阵【EASY】
二维数组的结构特性入手
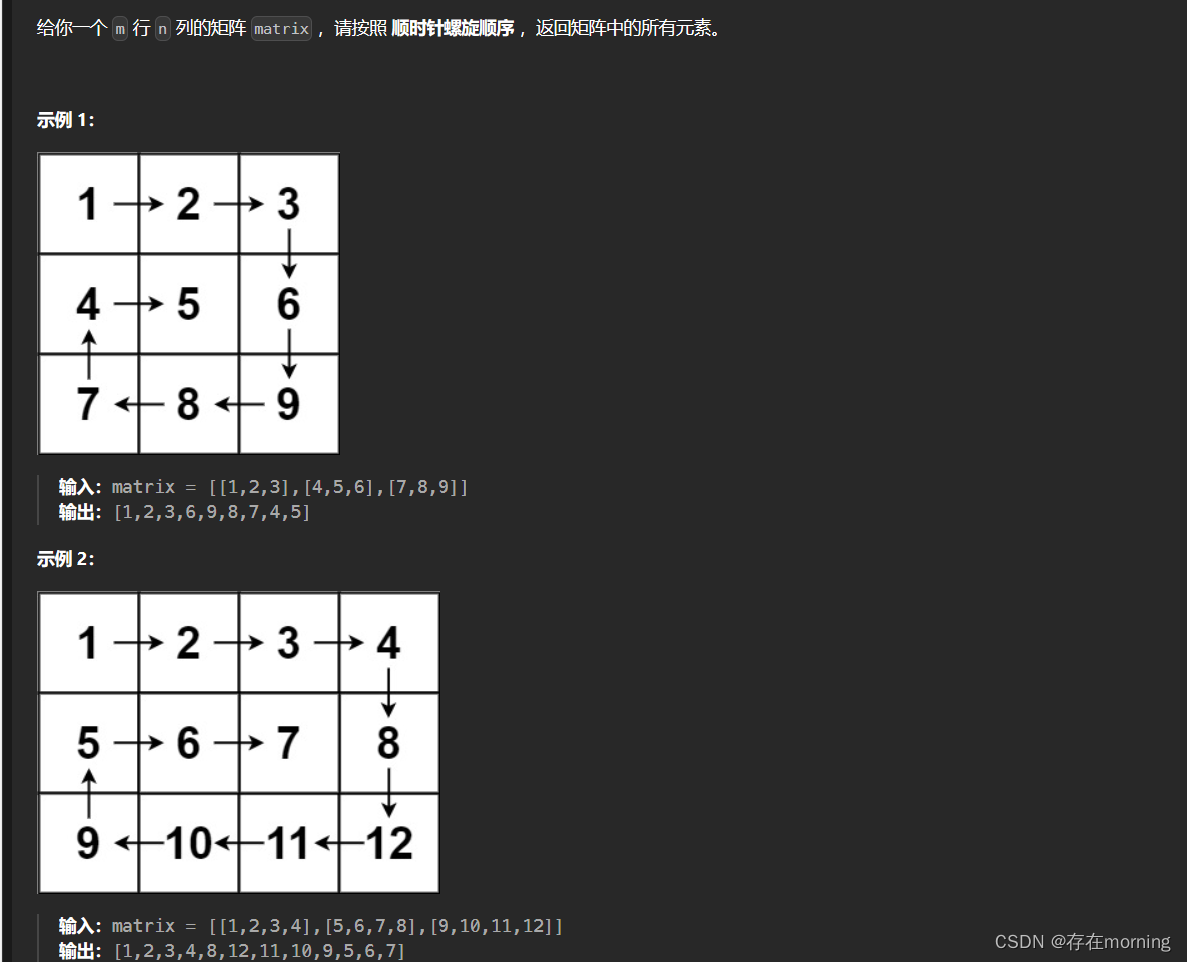
题干
解题思路
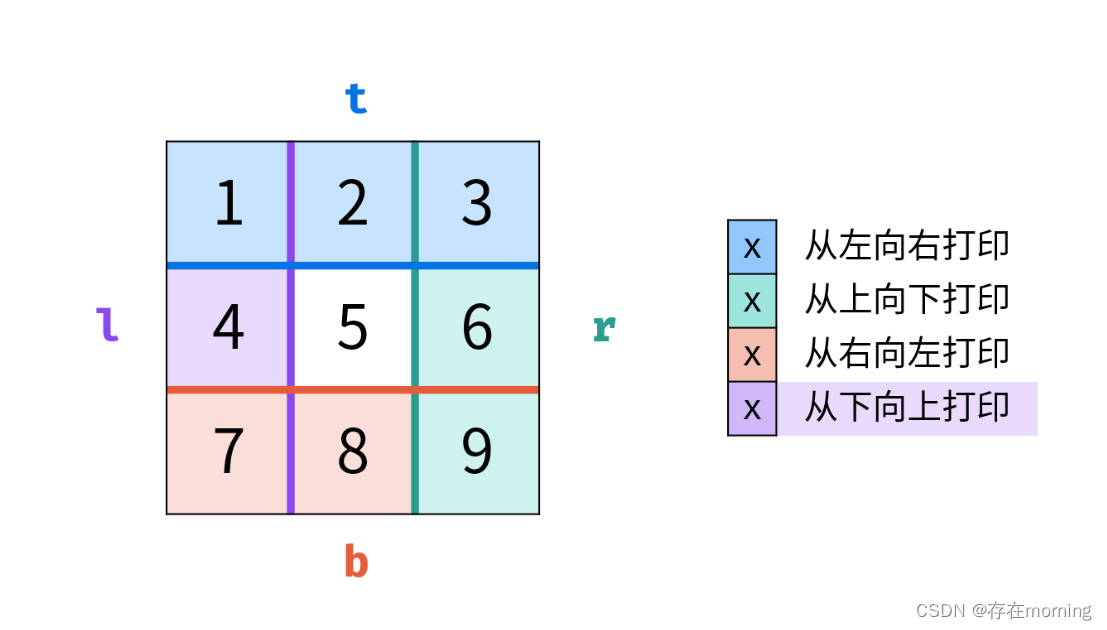
根据题目示例 matrix = [[1,2,3],[4,5,6],[7,8,9]] 的对应输出 [1,2,3,6,9,8,7,4,5] 可以发现,顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。
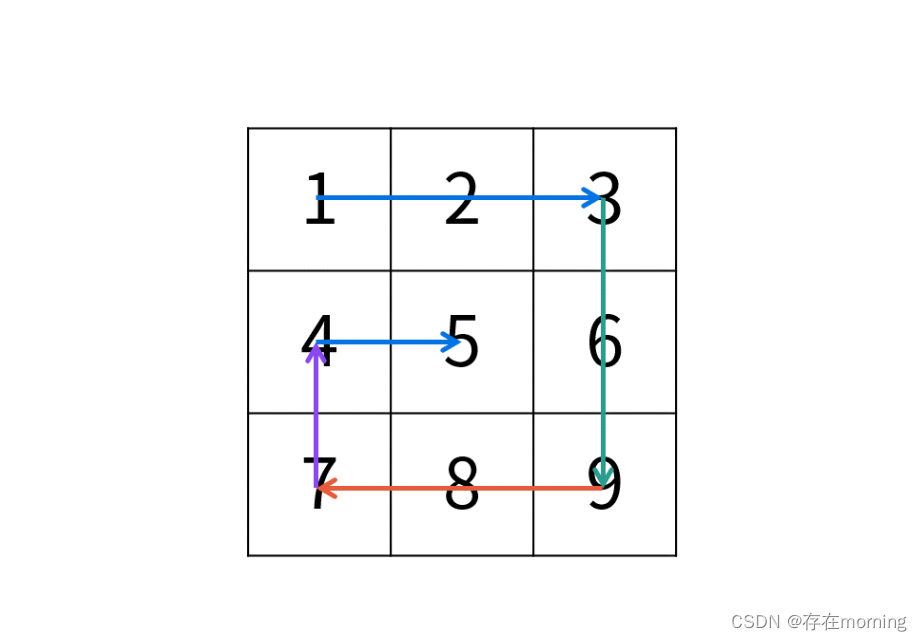
因此,考虑设定矩阵的 “左、上、右、下” 四个边界,模拟以上矩阵遍历顺序,算法流程:
- 空值处理: 当 matrix 为空时,直接返回空列表 [] 即可。
- 初始化: 矩阵 左、右、上、下 四个边界 l , r , t , b ,用于打印的结果列表 res 。
- 循环打印: “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印。
- 根据边界打印,即将元素按顺序添加至列表 res 尾部。
- 边界向内收缩 1 (代表已被打印)。
- ** 判断边界是否相遇**(是否打印完毕),若打印完毕代表下一个方向无需打印,则跳出。
- 返回值: 返回 res 即可。
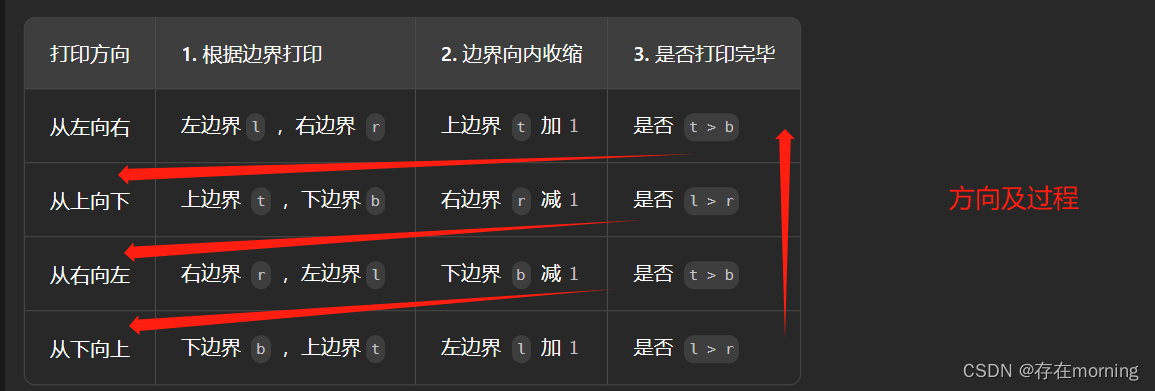
整体的打印过程
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param matrix int整型二维数组
* @return int整型ArrayList
*/
public ArrayList<Integer> spiralOrder (int[][] matrix) {
// 1 入参判断,如果为空数组,返回空集合
if (matrix.length < 1) {
return new ArrayList<Integer>();
}
// 2 定义四条边及返回值
ArrayList<Integer> result = new ArrayList<Integer>();
int left = 0;
int right = matrix[0].length - 1;
int top = 0;
int bottom = matrix.length - 1;
// 3 循环打印四条边
while (true) {
// 3-1 从左向右打印,明确左右边界,打印完后上边界向下移动,并判断是否有必要继续从上到下打印
for (int i = left; i <= right; i++) {
result.add(matrix[top][i]);
}
if (++top > bottom) {
break;
}
// 3-2 从上向下打印,明确上下边界,打印完后右边界向左移动,并判断是否有必要继续从右到左打印
for (int i = top; i <= bottom; i++) {
result.add(matrix[i][right]);
}
if (left > --right) {
break;
}
// 3-3 从右向左打印,明确左右边界,打印完后下边界向上移动,并判断是否有必要继续从下到上打印
for (int i = right; i >= left; i--) {
result.add(matrix[bottom][i]);
}
if (top > --bottom) {
break;
}
// 3-4 从下向上打印,明确上下边界,打印完后左边界向右移动,并判断是否有必要继续从左到右打印
for (int i = bottom; i >= top; i--) {
result.add(matrix[i][left]);
}
if (++left > right) {
break;
}
}
return result;
}
}
++top > bottom 等价于先给 top 自增 1 ,再判断++top > bottom 逻辑表达式
复杂度分析
- 时间复杂度 O(MN) : M,N分别为矩阵行数和列数。
- 空间复杂度 O(1) : 四个边界 l , r , t , b 使用常数大小的额外空间。
旋转图像
和螺旋矩阵类似,也是对一圈数值做处理
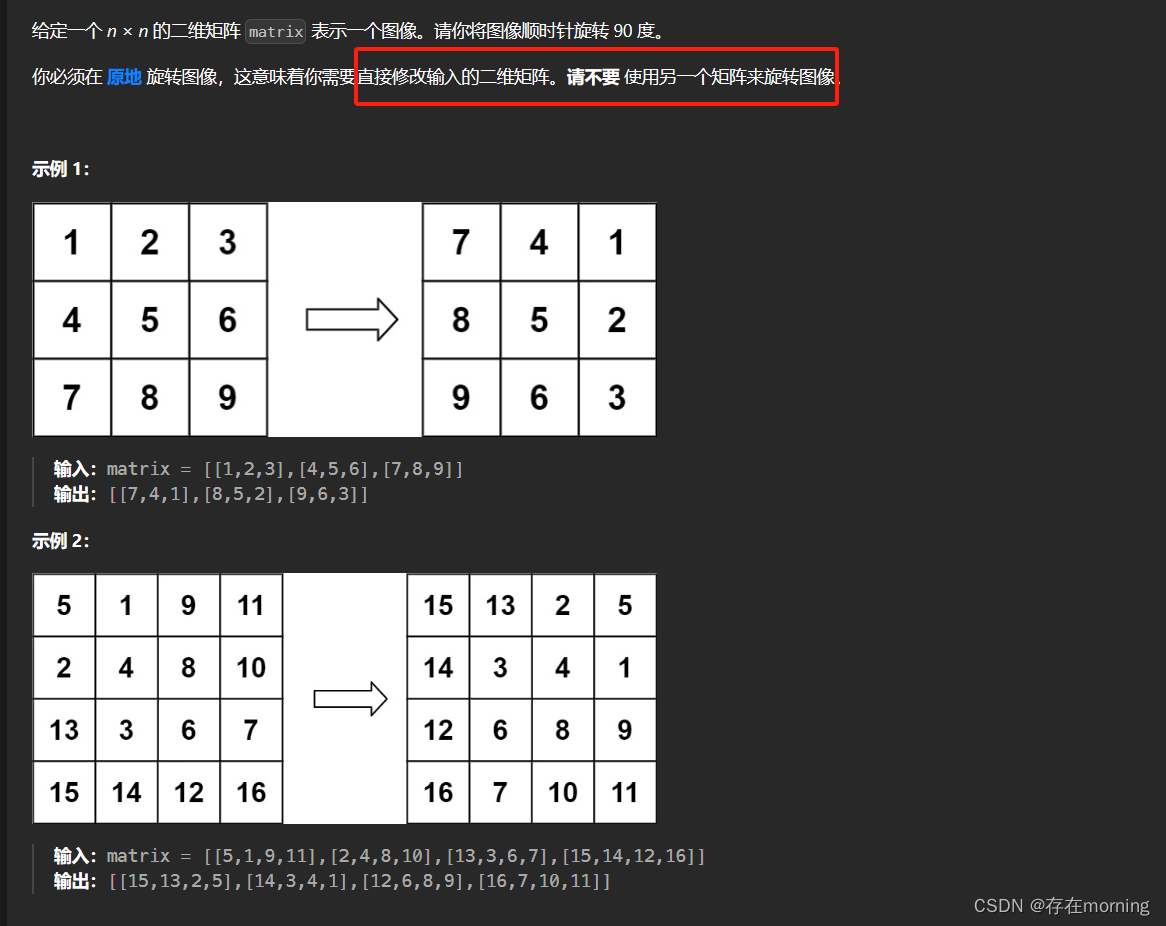
题干
解题思路
由原题知整体的旋转公式如下:

如果可以使用辅助矩阵则按如下方式修改即可:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 深拷贝 matrix -> tmp
int[][] tmp = new int[n][];
for (int i = 0; i < n; i++)
tmp[i] = matrix[i].clone();
// 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[j][n - 1 - i] = tmp[i][j];
}
}
}
}
考虑不借助辅助矩阵,通过在原矩阵中直接「原地修改」,实现空间复杂度 **O(1)**的解法。以位于矩阵四个角点的元素为例,设矩阵左上角元素 A 、右上角元素 B 、右下角元素 C 、左下角元素 D 。矩阵旋转 90º 后,相当于依次先后执行 D→A,C→D, B→C, A→B 修改元素,即如下「首尾相接」的元素旋转操作:

如上图所示,由于第 1 步 D→A已经将 A覆盖(导致 A 丢失),此丢失导致最后第 4步 A→B无法赋值。为解决此问题,考虑借助一个「辅助变量 tmp」预先存储 A ,此时的旋转操作变为:
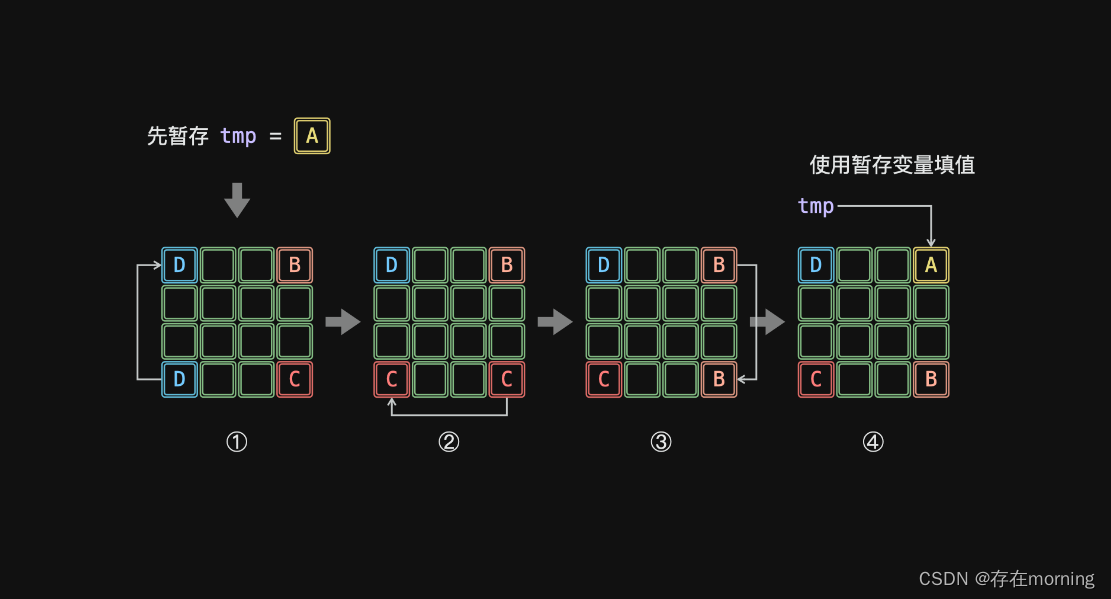
如上图所示,一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/4的各元素为起始点执行以上旋转操作,

将这些元素旋转完成即完成了整个数组的旋转

具体来看,当矩阵大小n为偶数时,行列均取前n/2,当矩阵大小为奇数时,行取n/2,列取(n+1)/2,因为为奇数时,中间的元素不需要旋转
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
class Solution {
public void rotate(int[][] matrix) {
// 1 获取数组长度,依据替换顺序位置matrix[i][j]->matrix[j][n-1-i]推导出ABCD位置
int n = matrix.length;
//int a=matrix[i][j];int b=matrix[j][n-1-i];int c=matrix[n-1-i][n-1-j];int d=matrix[n-1-j][i];
// 2 遍历行列,行取n/2,列取(n+1)/2 为了应对奇数长度的n
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1) / 2; j++) {
// 2-1 暂存A的位置,用来后续替换B
int temp = matrix[i][j];
// 2-2 D替换A
matrix[i][j] = matrix[n - 1 - j][i];
// 2-3 C替换D
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
// 2-4 B替换C
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
// 2-5 A替换B
matrix[j][n - 1 - i] = temp;
}
}
}
}
复杂度分析
时间复杂度 O(N*N): 其中 N 为输入矩阵的行(列)数。需要将矩阵中每个元素旋转到新的位置,即对矩阵所有元素操作一次,使用O(N*N)的时间
空间复杂度 O(1) : 临时变量 tmp使用常数大小的额外空间。值得注意,当循环中进入下轮迭代,上轮迭代初始化的 tmp占用的内存就会被自动释放,因此无累计使用空间。
搜索二维矩阵【MID】
从下题矩阵的特性入手进行查找
题干

解题思路
数组从左到右和从上到下都是升序的,如果从右上角出发开始遍历呢?会发现每次都是向左数字会变小,向下数字会变大,有点和二分查找树相似。二分查找树的话,是向左数字变小,向右数字变大。所以我们可以把 target 和当前值比较。
- 如果 target 的值大于当前值,那么就向下走。
- 如果 target 的值小于当前值,那么就向左走。
- 如果相等的话,直接返回 true 。
也可以换个角度思考
- 如果 target 的值大于当前值,也就意味着当前值所在的行肯定不会存在 target 了,可以把当前行去掉,从新的右上角的值开始遍历。
- 如果 target 的值小于当前值,也就意味着当前值所在的列肯定不会存在 target 了,可以把当前列去掉,从新的右上角的值开始遍历。
看下边的例子
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
如果 target = 9,如果我们从 15 开始遍历, cur = 15
target < 15, 去掉当前列, cur = 11
[1, 4, 7, 11],
[2, 5, 8, 12],
[3, 6, 9, 16],
[10, 13, 14, 17],
[18, 21, 23, 26]
target < 11, 去掉当前列, cur = 7
[1, 4, 7],
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
target > 7, 去掉当前行, cur = 8
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
target > 8, 去掉当前行, cur = 9, 遍历结束
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param target int整型
* @param array int整型二维数组
* @return bool布尔型
*/
public boolean Find (int target, int[][] array) {
// 1 入参判断
if (array.length < 1) {
return false;
}
// 2 定义行列边界,从右上角出发,所以初始化为右上角位置
int right = array[0].length - 1;
int top = 0;
// 3 出发开始遍历,明确左右边界的范围
while (right >= 0 && top <= array.length - 1) {
int curValue = array[top][right];
if (curValue > target) {
// 3-1 如果当前值大于目标值,舍弃本列
right--;
} else if (curValue < target) {
// 3-2 如果当前值小于目标值,舍弃本行
top++;
} else {
// 3-3 如果当前值等于目标值,找到了目标值
return true;
}
}
return false;
}
}
复杂度分析
- 时间复杂度 O(M+N) : 只遍历了一遍
- 空间复杂度 O(1) :没有使用额外空间。
拓展知识:二维数组
二维数组是一种常见的数据结构,它由多行和多列组成,可以用来存储和处理二维数据集合,例如矩阵、表格、图像、地图等。在不同的编程语言中,定义和使用二维数组的方式可能有所不同,以下是一些常见编程语言中的示例。
C/C++:
// 定义一个3x3的整数二维数组
int matrix[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
// 访问元素
int element = matrix[1][2]; // 获取第二行第三列的元素,值为6
Python:
# 定义一个3x3的整数二维数组(使用嵌套列表)
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
# 访问元素
element = matrix[1][2] # 获取第二行第三列的元素,值为6
Java:
// 定义一个3x3的整数二维数组
int[][] matrix = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
// 访问元素
int element = matrix[1][2]; // 获取第二行第三列的元素,值为6
常用方法和操作:
-
访问元素: 使用索引来访问二维数组中的特定元素,例如
matrix[i][j],其中i表示行号,j表示列号。 -
遍历二维数组: 使用嵌套循环来遍历二维数组,通常使用一个循环迭代行,另一个循环迭代列,以访问所有元素。
-
初始化: 在定义二维数组时,可以初始化数组的值。可以使用嵌套列表(Python)、嵌套数组(C/C++)或类似方式来初始化。
-
修改元素: 可以通过索引来修改特定元素的值,例如
matrix[i][j] = newValue。 -
获取数组的行数和列数: 可以使用数组的长度或大小来获取行数和列数。
-
在算法中使用: 二维数组在解决各种问题时非常有用,例如矩阵运算、图算法、迷宫求解等。
-
释放内存(C/C++): 在使用动态分配内存创建二维数组时,需要谨慎释放内存以防止内存泄漏。
二维数组是一种非常灵活和强大的数据结构,可以在各种应用中发挥作用,从简单的数据存储到复杂的算法实现。







![[MIT6.824] Lab 3: Fault-tolerant Key/Value Service](https://img-blog.csdnimg.cn/img_convert/6d7eacf1555fbc281d6d1155a635726e.png)
