图
- 图的基本概念
- 图的概念
- 顶点和边
- 有向图和无向图
- 完全图
- 有向完全图
- 无向完全图
- 邻接顶点
- 顶点的度
- 路径和路径长度
- 简单路径和回路
- 子图
- 生成树
- 连通图
- 强连通图
- 图的存储结构
- 邻接矩阵
- 邻接表
- 图的遍历
- BFS
- DFS
图的基本概念
图的概念
🚀图是由顶点集合及顶点间关系组成的一种数据结构: G = (V,E),其中:顶点集合V = {x|x属于某个数据对象集}是又穷非空集合;
E = {(x,y)|x,y属于V}或者E = {<x,y>|x,y属于V并且path(x,y)}是顶点间关系的有穷集合,也叫做边的集合。
(x,y)表示x与y间的一条双向通路,是没有方向的。<x,y>表示x到y的一条单项路径,是有方向的。
顶点和边
🚀图中的结点就是顶点,第i个顶点记作Vi。两个顶点Vi和Vj相关联称作顶点Vi和顶点Vj之间有一条边,第k条边记作Ek,Ek = (Vi,Vj)或者<Vi,Vj>。
有向图和无向图
🚀在有向图中,顶点对<x,y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边,<x,y>与<y,x>是两条不同的边。
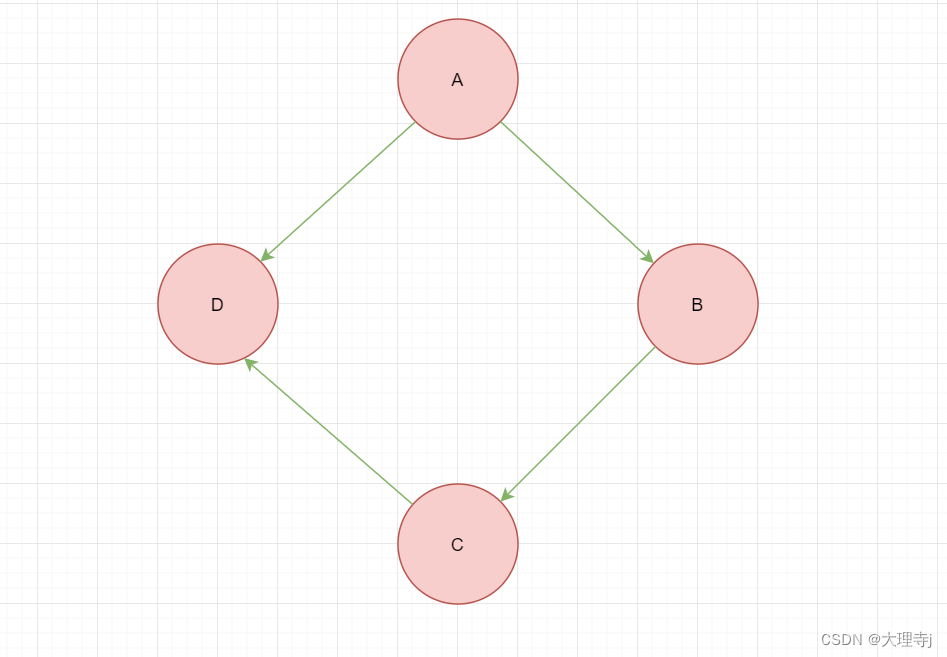
🚀在无向图中,顶点对(x,y)是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边是没有方向的,(x,y)与(y,x)是同一条边。

完全图
有向完全图
🚀在n个顶点的有向图中,存在n*(n - 1)条边,即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图。
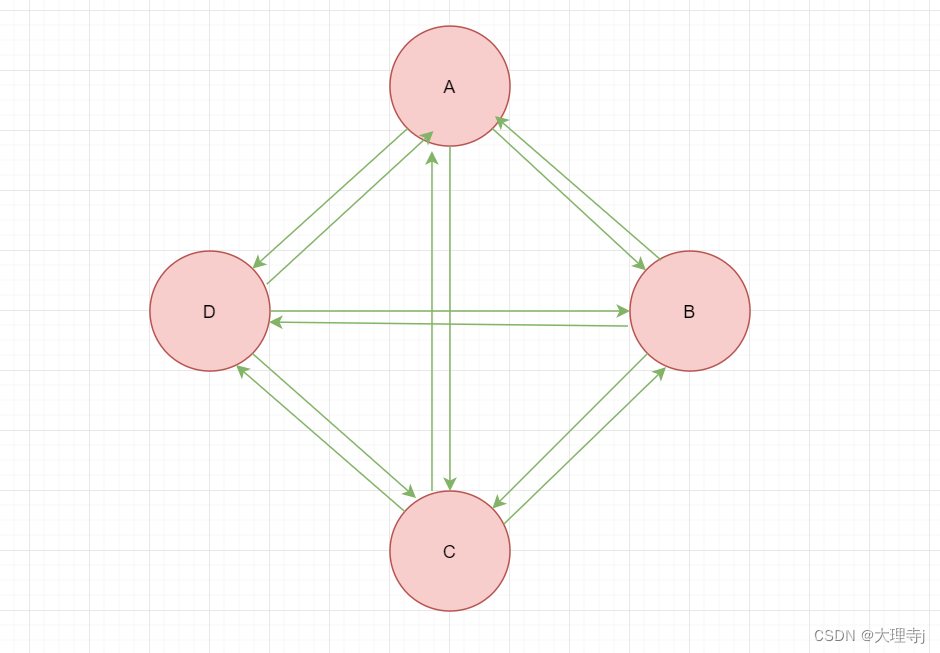
无向完全图
🚀在n个顶点的无向图中,存在n*(n - 1) / 2条边,即任意两个顶点之间有且只有一条边,则称此图为无向完全图。
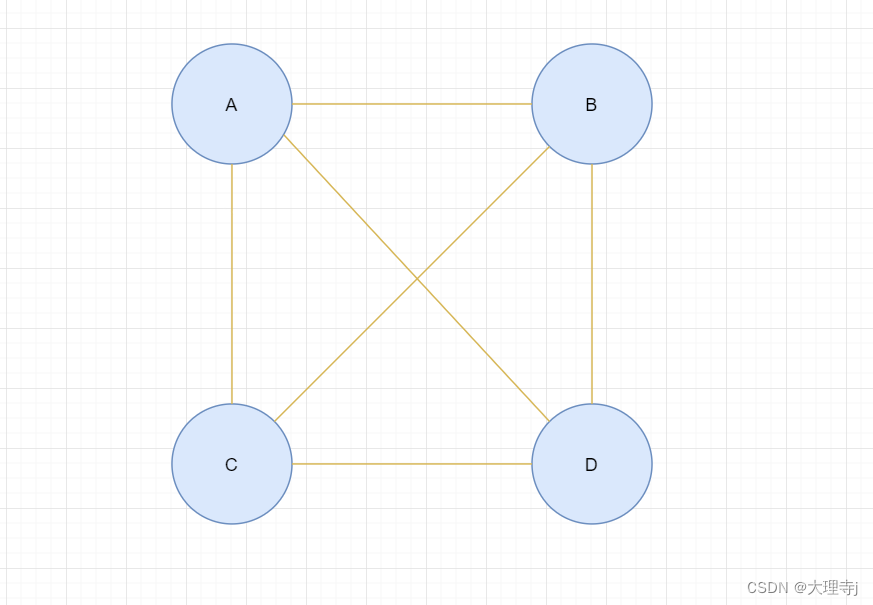
邻接顶点
🚀在无向图G中,若(u,v)是E(G)的一条边,则称u和v互为邻接顶点,并称边(u,v)依附于顶点u和v。在有向图G中,若<u,v>是E(G)中的一条边,则称顶点u邻接到v,v邻接自u,并称边<u,v>与顶点u和顶点v相关联。
顶点的度
🚀顶点的度是指与它相关联边的条数,记作dev(v)。在有向图中,顶点的度等于顶点的入度与顶点的出度之和,其中顶点v的入度是指以v为终点的有向边的条数,记作indev(v)。顶点v的出度是指以v为起点的有向边条数,记作outdev(v)。
🚀对于无向图顶点的度=顶点的入度=顶点的出度,即dev(u) = indev(u) = outdev(u)。
路径和路径长度
🚀在图G(V,E)中,若从顶点Vi出发有一组边可使其到达顶点Vj,则称顶点Vi到顶点Vj经过的顶点序列为Vi到Vj的路径。
🚀对于不带权值的图,路径长度是指该路径上边的条数。对于带权值的图,路径长度是指该路径上各个边上的权值综合。
简单路径和回路
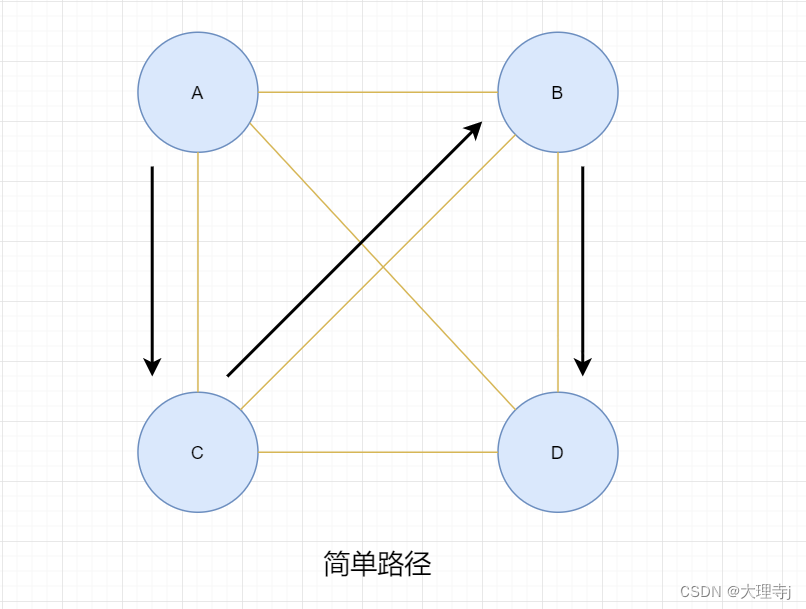
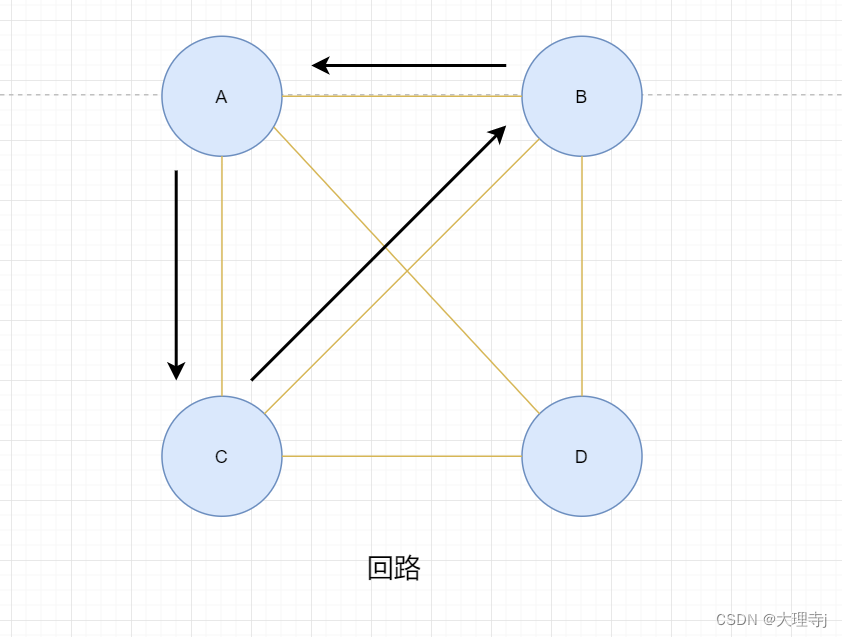
🚀若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路
径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
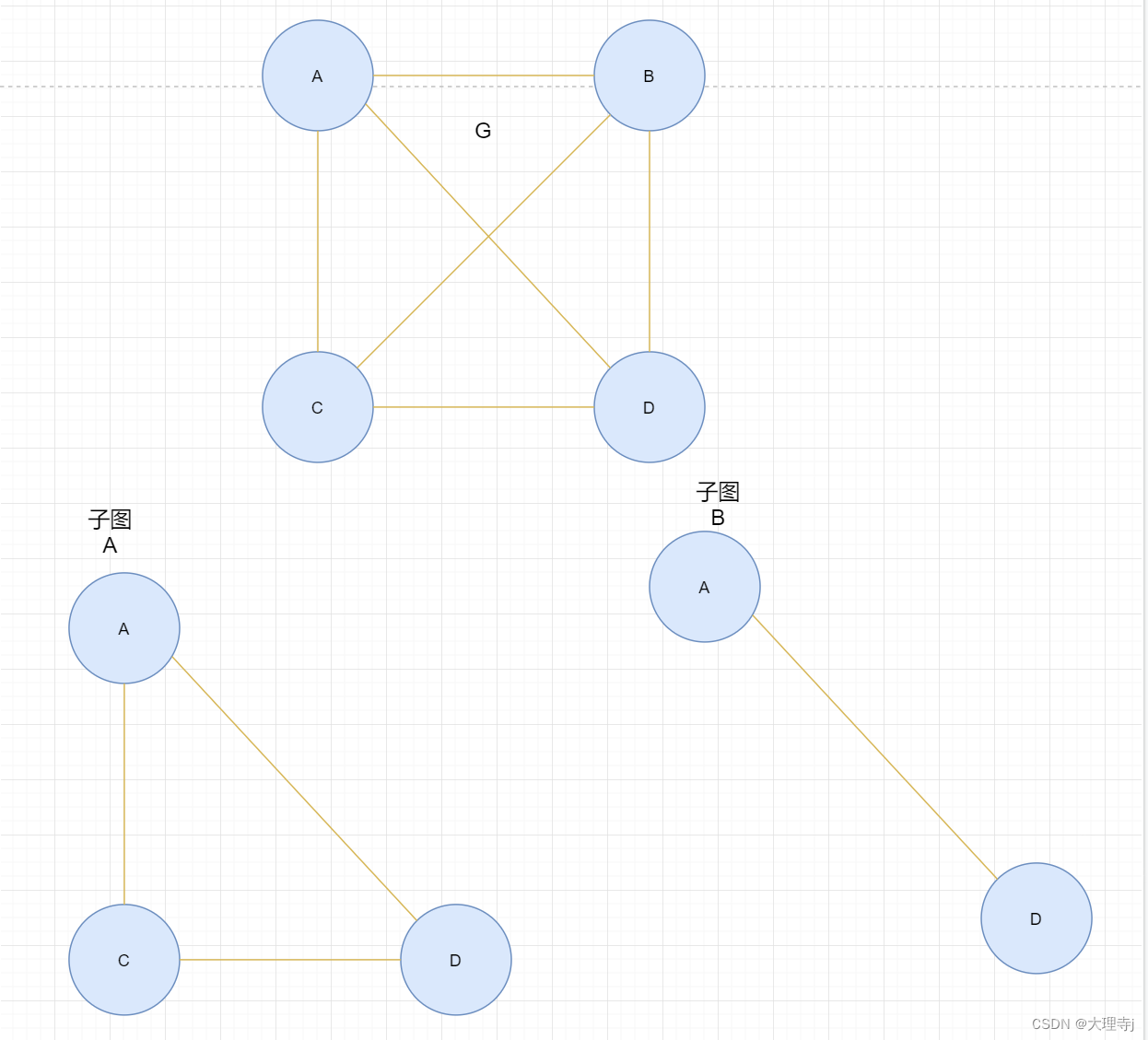
子图
🚀由一个图的若干个顶点和若干条边组成的新的图称为原图的子图。
生成树
🚀一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。
连通图
🚀在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
强连通图
🚀在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图是强连通图。
图的存储结构
邻接矩阵
🚀用一个二维数组来表示任意两点间的联通关系,用0或1表示,对于带权值的图来说如果两个点是来联通的那么邻接矩阵中存储的就是权值,不联通通常存的是无穷大。
🚀对于无向图来说,邻接矩阵是关于对角线对称的,有向图的邻接矩阵不一定是对称的。
🚀邻接矩阵的优点是能够迅速判断两个点的联通关系,缺点是当图结构中边的数量比较少时,是比较浪费空间的。所以邻接矩阵适合存储密集图。
namespace matrix {
template<typename V,typename W,W W_MAX = INT_MAX,bool direction = false>
class Graph {
typedef Graph<V, W, W_MAX, direction> self;
private:
std::vector<V> _vertex; //存储顶点
std::unordered_map<V, int> _index_map; //存储顶点和下标的映射关系
std::vector<std::vector<W>> _matrix; //邻接矩阵
public:
Graph(const V* v,size_t n) {
//顶点集合
_vertex.reserve(n);
for (int i = 0; i < n; i++) {
_vertex.push_back(v[i]);
_index_map[v[i]] = i;
}
//邻接矩阵初始化
_matrix.resize(n);
for (int i = 0; i < n; i++) {
_matrix[i].resize(n,W_MAX);
}
}
Graph() = default; //默认构造
size_t GetVertexIndex(const V& v) {
auto it = _index_map.find(v);
if (_index_map.end() != it) {
return it->second;
}
else {
throw std::invalid_argument("没有此顶点");
return -1;
}
}
void _AddEdge(size_t srci, size_t dsti, const W& w) {
_matrix[srci][dsti] = w;
if (false == direction) {
_matrix[dsti][srci] = w;
}
}
void AddEdge(const V& src, const V& dst, const W& w) {
size_t srci = this->GetVertexIndex(src);
size_t dsti = this->GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}
void PrintGraph() {
//打印顶点与下标的映射关系
for (int i = 0; i < _vertex.size(); i++) {
std::cout << "[" << _vertex[i] << "]->" << i << std::endl;
}
//打印邻接矩阵
std::cout << " ";
for (int i = 0; i < _vertex.size(); ++i) {
//std::cout << i << " ";
printf("%-4d", i);
}
std::cout << "\n";
for (int i = 0; i < _matrix.size(); ++i) {
std::cout << i << " ";
for (int j = 0; j < _matrix[i].size(); ++j) {
if (i == j) {
//std::cout << 0;
printf("%-4d", 0);
}
else {
if (_matrix[i][j] == W_MAX) {
//std::cout << "# ";
printf("%-4c",'#');
}
else {
//std::cout << _matrix[i][j] << " ";
printf("%-4d", _matrix[i][j]);
}
}
}
std::cout << "\n";
}
}
};
}
邻接表
🚀邻接表表示法,用数组表示顶点的集合,使用链表存储边的关系。
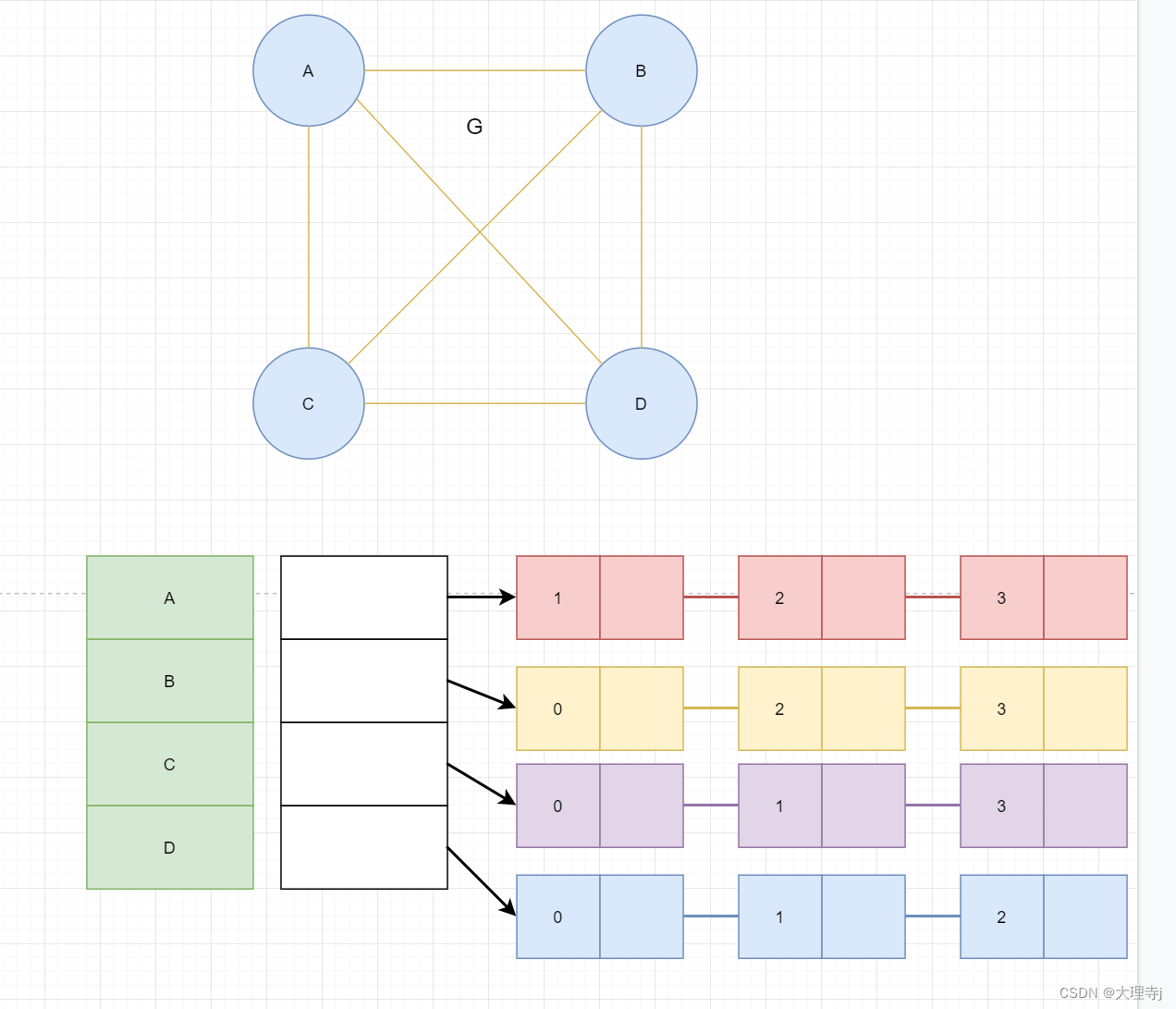
🚀无向图的邻接表,同一条边会出现两次。如果想知道一个顶点的度,只需要知道该顶点Vi边链表集合中的边数目即可。
🚀用邻接表表示法,可以轻松的找到与顶点相连的边,但是不能够立即判断两个点的联通关系。邻接表适合存储稀疏图。
namespace link_table {
template<typename W>
struct Edge {
size_t _dsti;
W _weight;
Edge<W>* _next;
Edge(size_t dsti,const W& weight) :_dsti(dsti),_weight(weight) {}
};
template<typename V, typename W,bool direction = false>
class Graph {
typedef Edge<W> Edge;
private:
std::vector<V> _vertex; //存储顶点
std::unordered_map<V, int> _index_map; //存储顶点和下标的映射关系
std::vector<Edge*> _tables; //邻接表
public:
Graph(const V* v, size_t n) {
//顶点集合
_vertex.reserve(n);
for (int i = 0; i < n; i++) {
_vertex.push_back(v[i]);
_index_map[v[i]] = i;
}
//邻接表初始化
_tables.resize(n, nullptr);
}
size_t GetVertexIndex(const V& v) {
auto it = _index_map.find(v);
if (_index_map.end() != it) {
return it->second;
}
else {
throw std::invalid_argument("没有此顶点");
return -1;
}
}
void AddEdge(const V& src, const V& dst, const W& w) {
size_t srci = this->GetVertexIndex(src);
size_t dsti = this->GetVertexIndex(dst);
Edge* peg = new Edge(dsti,w);
peg->_next = _tables[srci];
_tables[srci] = peg;
if (false == direction) {
Edge* peg = new Edge(srci,w);
peg->_next = _tables[dsti];
_tables[dsti] = peg;
}
}
void PrintGraph() {
//打印顶点与下标的映射关系
for (int i = 0; i < _vertex.size(); i++) {
std::cout << "[" << _vertex[i] << "]->" << i << std::endl;
}
//打印邻接表
for (int i = 0; i < _vertex.size(); ++i) {
std::cout << "[" << _vertex[i] << ":" << i << "]->";
Edge* cur = _tables[i];
while (cur) {
std::cout << "[" << _vertex[cur->_dsti] << ":" << cur->_dsti << ":" << cur->_weight << "]->";
cur = cur->_next;
}
std::cout << "null\n";
}
}
};
}
图的遍历
BFS
🚀图的广度优先遍历与二叉树的广度优先遍历类似,不同点就是对于二叉树而言,每个结点至多有左右子树与其相连,但是图中的某个结点,其邻接点的个数是不确定的,并且在图的遍历中会使用一个标记数组来标识某个顶点是否被访问过(防止重复遍历,甚至出现死循环的现象)。
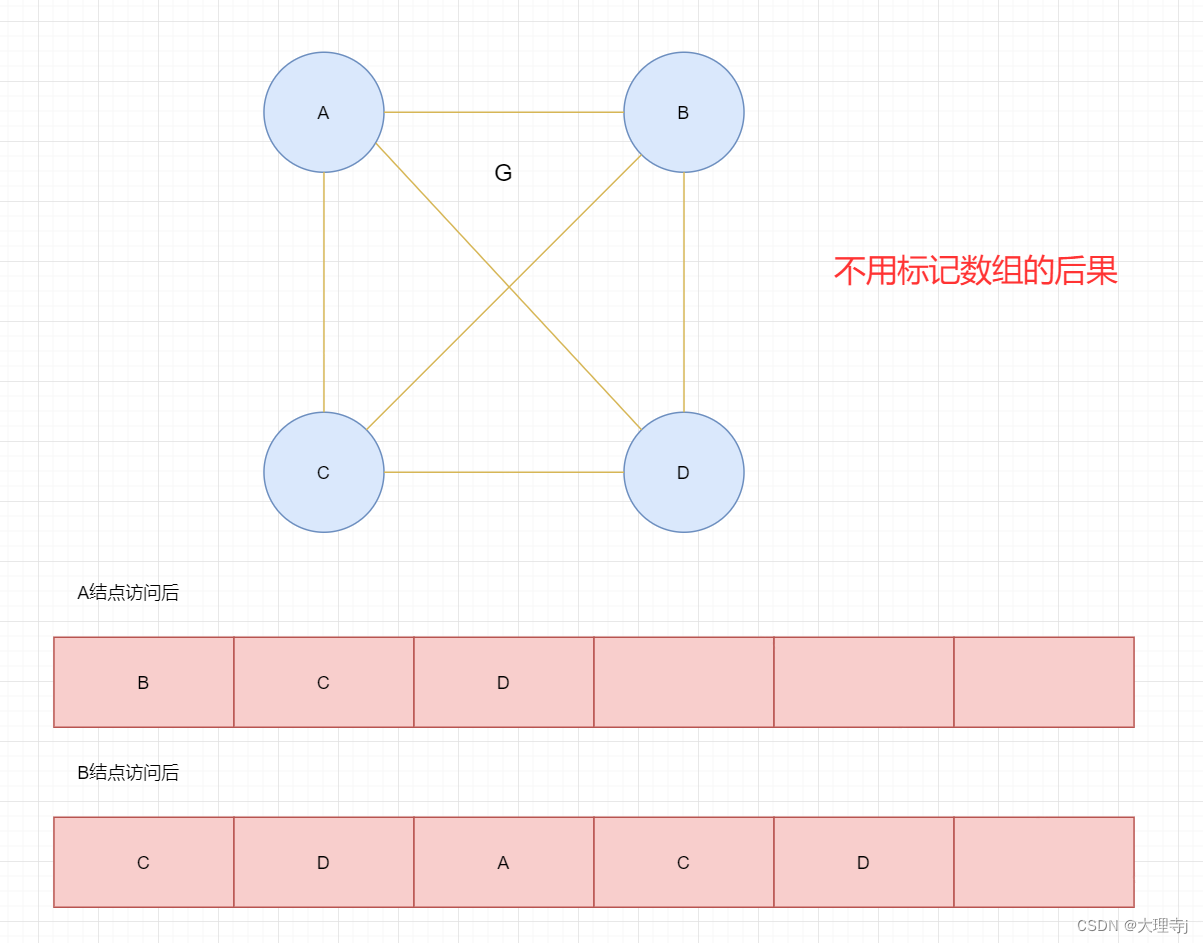
🚀代码实现:
void BFS(const V& src) {
size_t n = _vertex.size();
std::vector<bool> visit(n,false);
std::queue<size_t> q;
size_t srci = GetVertexIndex(src);
q.push(srci);
visit[srci] = true;
size_t level_size = 1;
int cnt = 1;
//一直循环到队列为空,每次取出一个结点并把其临接点带入队列
while (!q.empty()) {
std::cout << "第" << cnt++ << "层: ";
for (int j = 0; j < level_size; ++j) {
size_t top = q.front();
q.pop();
std::cout << "[" << top << ":" << _vertex[top] << "]-";
for (int i = 0; i < n; i++) {
if (_matrix[top][i] != W_MAX && visit[i] != true) {
q.push(i);
visit[i] = true;
}
}
}
std::cout << "null\n";
level_size = q.size();
}
}
DFS
🚀深度优先遍历的原则就是,一条路走到黑,访问完起始结点的邻接点后,就以邻接点为新的起始结点继续向下访问,知道条件不满足时,再返回到上一层函数栈帧中。同样,深度优先遍历也需要一个标记数组来标记一个顶点是否被访问过。
🚀代码实现:
void _DFS(size_t srci, std::vector<bool>& visit) {
std::cout << "[" << srci << ":" << _vertex[srci] << "]\n";
visit[srci] = true;
for (int i = 0; i < _vertex.size(); ++i) {
if (_matrix[srci][i] != W_MAX && visit[i] != true) {
_DFS(i, visit);
}
}
}
void DFS(const V& src) {
size_t n = _vertex.size();
size_t srci = GetVertexIndex(src);
std::vector<bool> visit(n, false);
_DFS(srci, visit);
}