归并排序含非递归版

news2024/10/7 8:26:45

1.归并排序的原理

2.实现归并排序

2.1框架

2.2区间问题和后序遍历

2.3归并并拷贝

2.4归并排序代码

2.5测试

3.非递归实现归并排序

3.1初次实现

3.2测试

3.3修改

3.4修改测试

1.归并排序的原理

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；

即先使每个子序列有序，再使子序列段间有序 若将两个有序表合并成一个有序表，称为二路归并。

可以将数组内容想象成一颗二叉树，通过递归的方式将数组的内容分为左子树和右子树，分出来的左子树和右子树又分别有它们的左子树和右子树。不断地向下进行拆分，直到拆分到没有对应区间和区间只有一个元素(有序)的时候便递归返回。然后使用归并的方式将左子树和右子树归并成有序数组，再将其拷贝会原数组，这样对应的子树便会有序，再递归返回，不断地递归。直到根左子树和根右子树有序，再归并和拷贝，整个数组就会变得有序。

如图所示：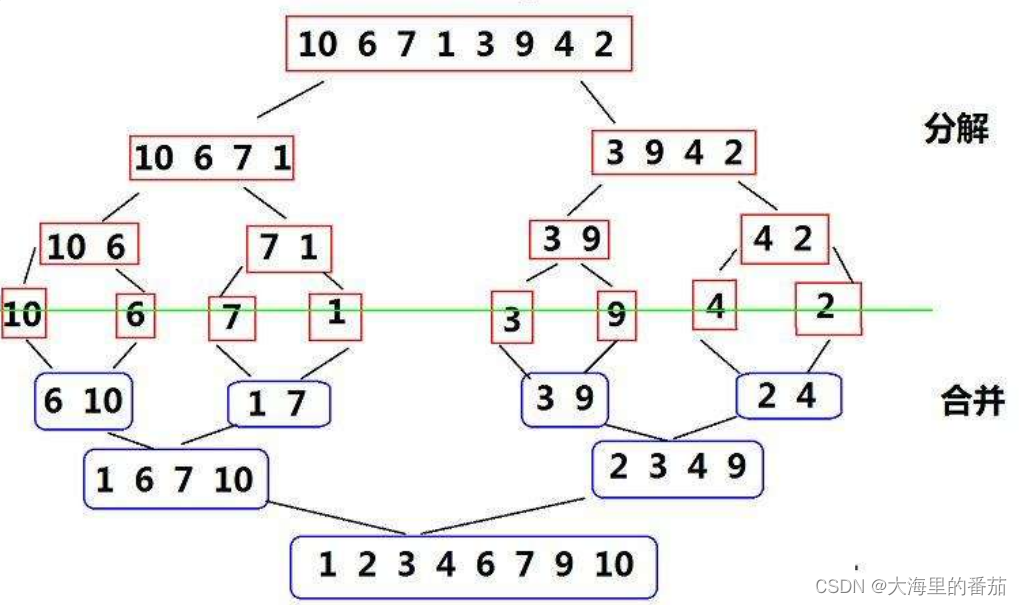

2.实现归并排序

归并排序需要开额外的空间来辅助实现 之所以不在原数组实现，是因为如果你使用交换的方式来进行排序，可能会将原数组已经排好序的部分又一次变回无序，而使用令数组向后移动的方式进行对应的排序，时间复杂度便会大大增加，因此归并排序可以理解成一种以空间换时间的排序方法。

归并排序需要开额外的空间，但每次递归都要开空间显然是不合理的，因此我们使用一个函数来完成递归的部分。思考一下，新创建的函数的参数应该有哪些，首先得有原数组，其次得有我们开辟好的数组，而我们要如二叉树一般形成对应的递归，显然需要区间，而区间的形成需要两个数来辅助，因此可以传递两个代表区间的数进来，可以取名为begin，end(left,right)，这样理解起来轻松一些。

2.1框架

2.2区间问题和后序遍历

如二叉树一般实现后序遍历注意：当begin>=end时代表着区间不存在或者只有一个元素(有序)的时候返回。因为是后序遍历，需要先将区间的分界给计算出来之后才能使用。

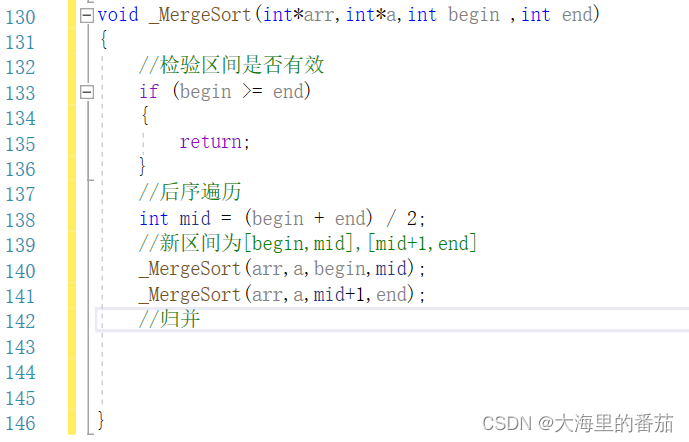
2.3归并并拷贝

可以看出，每次递归都会有两个区间的生成[begin,mid]和[mid+1,end]我们的目标就是将这两个区间归并在一起，这个很简单，循环便可以搞定。注意：两个区间不知道是哪个区间先完成循环，因此在外面需要将未完成循环的区间，补充回辅助数组中。

搞定完归并后，使用memcpy将辅助数组中的内容拷贝回原数组，排序便结束了。注意：我们传递的是闭区间，因此拷贝的长度为，end-begin+1

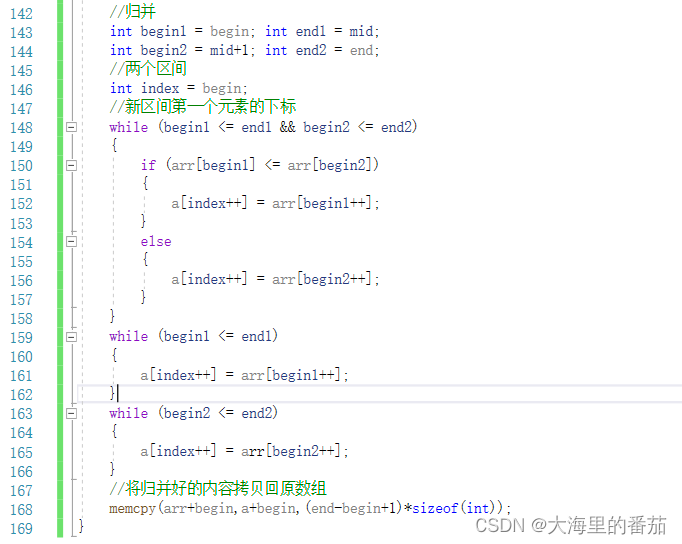
2.4归并排序代码

void MergeSort(int*arr,int n)
//将数组和数组的元素个数传递过来
{
	int* a = (int*)malloc(sizeof(int)*n);
	//创建辅助数组
	if (a == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(arr,a,0,n-1);
    free(a);
}
void _MergeSort(int*arr,int*a,int begin ,int end)
{
	//检验区间是否有效
	if (begin >= end)
	{
		return;
	}
	//后序遍历
	int mid = (begin + end) / 2;
	//新区间为[begin,mid],[mid+1,end]
	_MergeSort(arr,a,begin,mid);
	_MergeSort(arr,a,mid+1,end);
    //归并
	int begin1 = begin; int end1 = mid;
	int begin2 = mid+1; int end2 = end;
	//两个区间
	int index = begin;
	//新区间第一个元素的下标
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] <= arr[begin2])
		{
			a[index++] = arr[begin1++];
		}
		else
		{
			a[index++] = arr[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		a[index++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		a[index++] = arr[begin2++];
	}
	//将归并好的内容拷贝回原数组
	memcpy(arr+begin,a+begin,(end-begin+1)*sizeof(int));
}

2.5测试

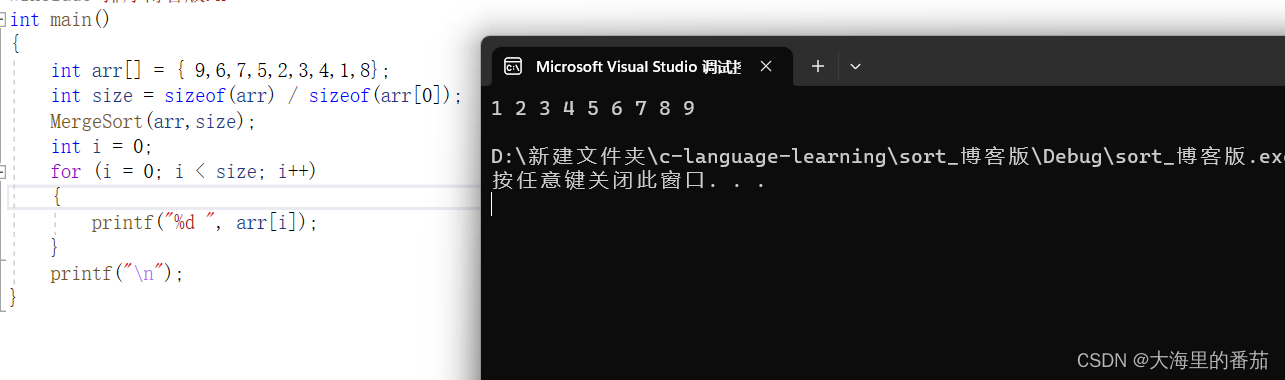
3.非递归实现归并排序

根据我们之前的排序我们可以看到它的本质是和预排序差不多的形态，因此我们可以通过一个整型如gap来区分一个元素和一个元素排序，两个元素和两个元素排序.......

3.1初次实现

void MergeSortNonR(int* arr, int n)
{
	int* a = (int*)malloc(sizeof(int) * n);
	//创建辅助数组
	int gap = 1;
	//gap=1便是1个元素和1个元素归并
	while (gap < n)
	{
		int i = 0;
		for (i = 0; i < n; i += 2 * gap)
			//i+=2*gap跳过一整个区间
		{
			//两个区间
			int begin1 = i; int end1 = i + gap - 1;
			int begin2 = i + gap; int end2 = i + 2 * gap - 1;
			int index = i;	//新区间第一个元素的下标
			//归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] <= arr[begin2])
				{
					a[index++] = arr[begin1++];
				}
				else
				{
					a[index++] = arr[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				a[index++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				a[index++] = arr[begin2++];
			}
			memcpy(arr + i, a + i, sizeof(int) * (2 * gap));
		}
		gap *= 2;
	}
	free(a);
}

3.2测试

出现了越界问题

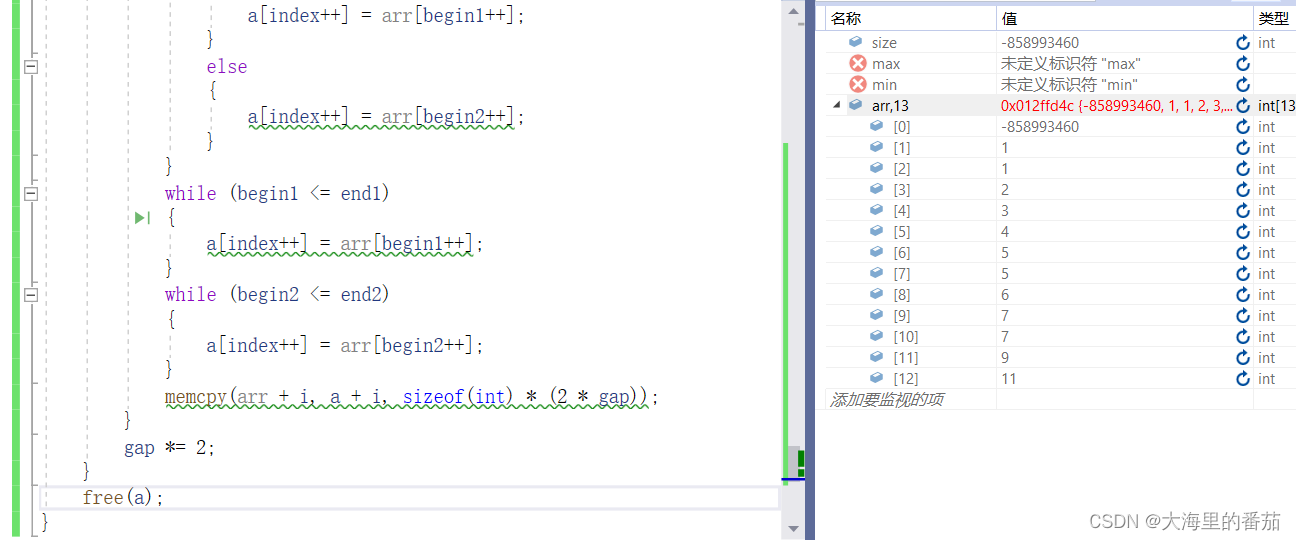
程序在打印之前就被迫中止了

3.3修改

观察可以发现，第一个区间的为[begin1,end1]，第二个区间为[begin2,end2]，那么begin1必然不会越界，而end1和更后面的begin2，end2都可能会越界。而其中end1和begin2越界的话都在说明已经排好序了，而end2越界，begin2没越界，则在说明还有数据未被排序。

再想一想细节，end1越界了，begin2一定越界，而begin2越界，end1不一定越界，所以无需考虑end1越界，只要begin2越界就说明排序已完成直接break 而只有end2越界，便将end2修正成数组的最大下标即可。

注意：我们之前使用拷贝函数均是拷贝2*gap个过去，在这里显然不合适，总区间长度应修正为end2-begin1，这个修正不应该放在最后，因为在进行归并的期间，begin1会++至end1 也不应该放在判断begin2，end2越界之前，因为可能会对end2进行修正。综上所述，得出的代码为

void MergeSortNonR(int* arr, int n)
{
	int* a = (int*)malloc(sizeof(int) * n);
	//创建辅助数组
	int gap = 1;
	//gap=1便是1个元素和1个元素归并
	while (gap < n)
	{
		int i = 0;
		for (i = 0; i < n; i += 2 * gap)
			//i+=2*gap跳过一整个区间
		{
			//两个区间
			int begin1 = i; int end1 = i + gap - 1;
			int begin2 = i + gap; int end2 = i + 2 * gap - 1;
			if (begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
				end2 = n - 1;//修正区间长度
			int order = end2 - begin1+1;//修正要拷贝的长度
			int index = i;	//新区间第一个元素的下标
			//归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] <= arr[begin2])
				{
					a[index++] = arr[begin1++];
				}
				else
				{
					a[index++] = arr[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				a[index++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				a[index++] = arr[begin2++];
			}
			/*int order = 2 * gap;
			if (2 * gap >= n)
			{
				order = n;
			}*/
			memcpy(arr + i, a + i, sizeof(int) * order);
		}
		gap *= 2;
	}
	free(a);
}