特征值与特征向量
设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式:
A x = λ x ( 1 ) Ax = \lambda x\quad\quad(1) Ax=λx(1)
则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x x x 称为矩阵 A A A 的特征向量.
关系式(1)推导得到 ( A − λ E ) x = 0 (A - \lambda E)x = 0 (A−λE)x=0,存在非零解 x x x 的充分必要条件为系数行列式为零:
∣ A − λ E ∣ = 0 ( 2 ) |A-\lambda E| = 0\quad\quad(2) ∣A−λE∣=0(2)
上式是以 λ \lambda λ 为未知数的一元 n 次方程,称为矩阵 A A A 的特征方程。特征方程在复数范围内恒有解,解的个数为方程的次数(重根按重数计算),因此,n 阶矩阵 A A A 在复数范围内有 n 个特征值。
设 n 阶矩阵 A = ( a i j ) A = (a_{ij}) A=(aij) 的特征值为 λ 1 , λ 2 , . . . , λ n \lambda_1, \lambda_2,...,\lambda_n λ1,λ2,...,λn
- ∑ i = 1 n λ i = ∑ i = 1 n a i i = t r ( A ) \sum_{i=1}^n\lambda_i = \sum_{i=1}^na_{ii} = tr(A) ∑i=1nλi=∑i=1naii=tr(A)
- ∏ i = 1 n λ i = ∣ A ∣ \prod_{i=1}^n\lambda_i = |A| ∏i=1nλi=∣A∣
- A 可逆的充分必要条件是 n 个特征值全不为零
有如下性质:
- 设 λ \lambda λ 是方阵 A A A 的特征值,则 λ 2 \lambda^2 λ2 是 A 2 A^2 A2 的特征值;当 A A A 可逆时, 1 / λ 1/\lambda 1/λ 是 A − 1 A^{-1} A−1的特征值.
A , B A,B A,B 都是 n 阶矩阵,若有可逆矩阵 P P P ,使:
P − 1 A P = B P^{-1}AP = B P−1AP=B
则称 B 是 A 的相似矩阵。 P − 1 A P P^{-1}AP P−1AP 称为 A 的相似变换。
定理:相似矩阵的特征值相同.
对于 n 阶矩阵 A , 若存在矩阵 P 满足 P − 1 A P = Λ P^{-1}AP =\Lambda P−1AP=Λ,则称矩阵 A 可对角化。
定理:一个 n 阶方阵 A 如果有 n 个不同的特征值,那么对应的 n 个特征向量互相线性独立
定理:任何 n 阶对称矩阵都有 n 个独立且正交的特征向量
图解特征值的含义:
| A | 特征值&特征向量 | x | Ax |
|---|---|---|---|
| [ 0.5 1 0 2 ] \begin{bmatrix} 0.5 & 1 \\ 0 & 2 \end{bmatrix} [0.5012] | λ 1 = 0.5 , p 1 = [ 1 , 0 ] T λ 2 = 2 , p 2 = [ 0 , 1 ] T \lambda_1 = 0.5, p_1 = [1, 0]^T \\ \lambda_2= 2, p_2 = [0, 1]^T λ1=0.5,p1=[1,0]Tλ2=2,p2=[0,1]T | 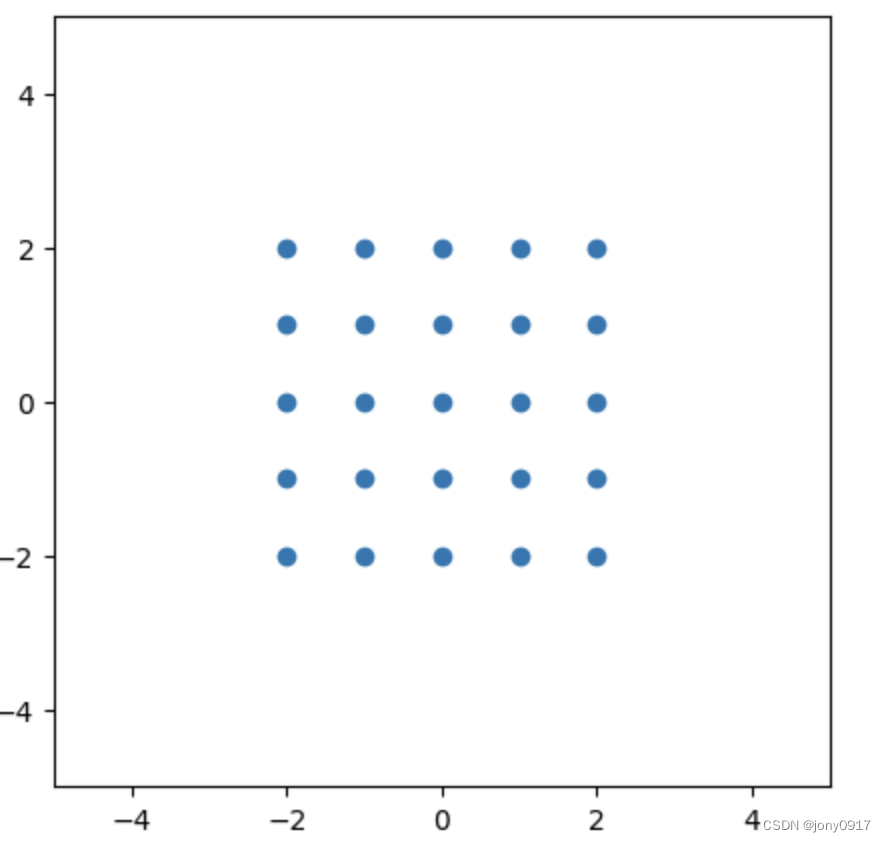 | 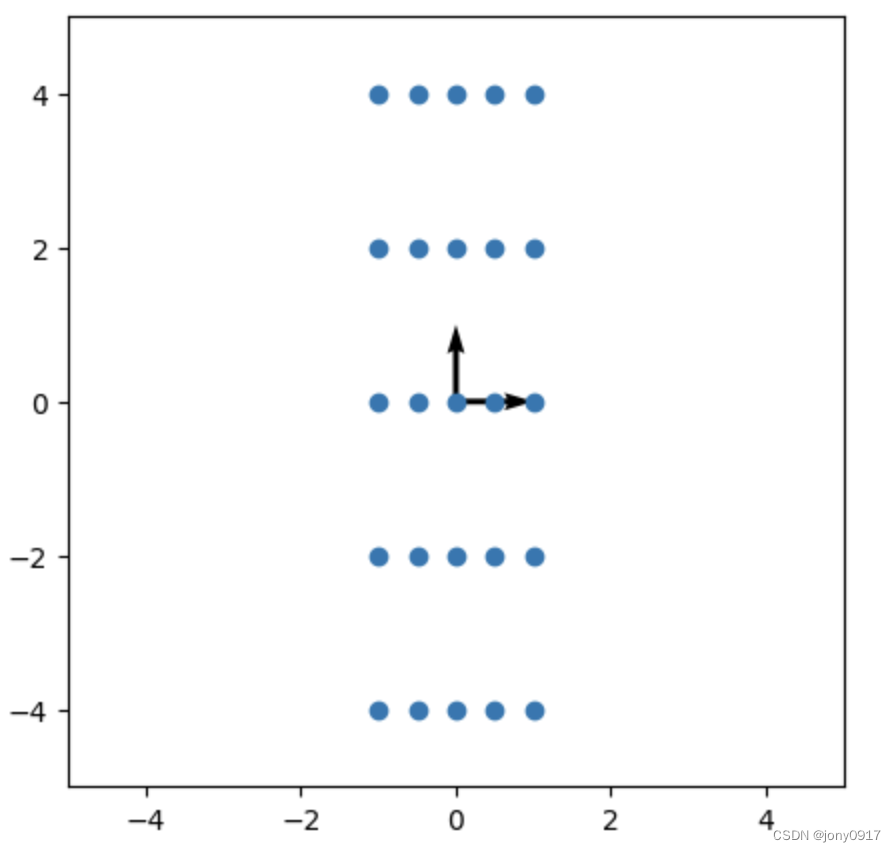 |
| [ 1 − 1 − 1 1 ] \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} [1−1−11] | λ 1 = 0 , p 1 = [ 1 , 1 ] T λ 2 = 2 , p 2 = [ − 1 , 1 ] T \lambda_1 = 0, p_1 = [1, 1]^T \\ \lambda_2= 2, p_2 = [-1, 1]^T λ1=0,p1=[1,1]Tλ2=2,p2=[−1,1]T |  | 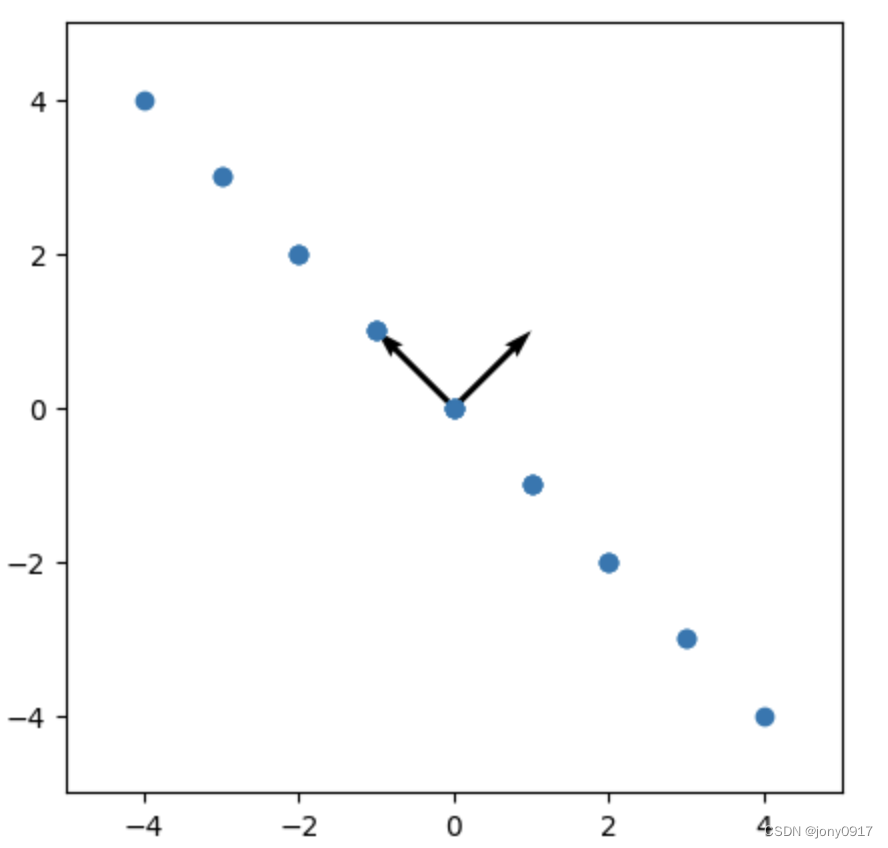 |
| [ 3 − 1 − 1 3 ] \begin{bmatrix} 3 & -1 \\ -1 & 3 \end{bmatrix} [3−1−13] | λ 1 = 2 , p 1 = [ 1 , 1 ] T λ 2 = 4 , p 2 = [ − 1 , 1 ] T \lambda_1 = 2, p_1 = [1, 1]^T \\ \lambda_2= 4, p_2 = [-1, 1]^T λ1=2,p1=[1,1]Tλ2=4,p2=[−1,1]T |  | 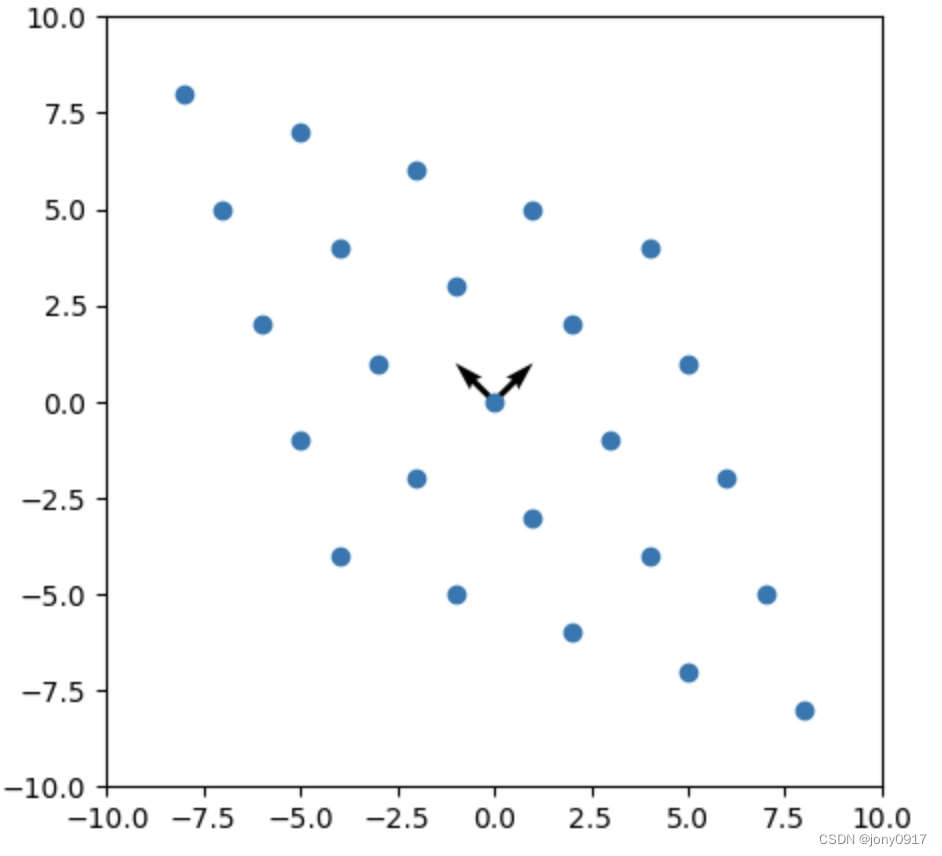 |
Cholesky 分解(Cholesky Decomposition)
把一个对称正定的矩阵表示成一个下三角矩阵 L 与其转置的乘积的形式。
A = L L T A = LL^T A=LLT
特征值分解(Eigen Decomposition)
对角化条件:当且仅当A满秩(有n个独立的特征向量)时,有 A = P − 1 D P A = P^{-1}DP A=P−1DP,P 为A的特征矩阵组成的可逆矩阵,D是有A的特征值组成的对角矩阵。
任何对称矩阵都可以对角化:
S = P D P − 1 S = PDP^{-1} S=PDP−1
其中 P 是由 n 个正交特征向量组成的矩阵,D 是有特征值组成的对角矩阵。
图解特征值分解:
| S = P D P − 1 S=PDP^{-1} S=PDP−1 | x | P − 1 x P^{-1}x P−1x | D P − 1 x DP^{-1}x DP−1x | P D P − 1 x PDP^{-1}x PDP−1x |
|---|---|---|---|---|
|
[
2
−
1
−
1
2
]
=
\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} =
[2−1−12]= [ 1 1 1 − 1 ] [ 1 0 0 3 ] [ 1 2 1 2 1 2 − 1 2 ] \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}\begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \end{bmatrix} [111−1][1003][212121−21] |  | 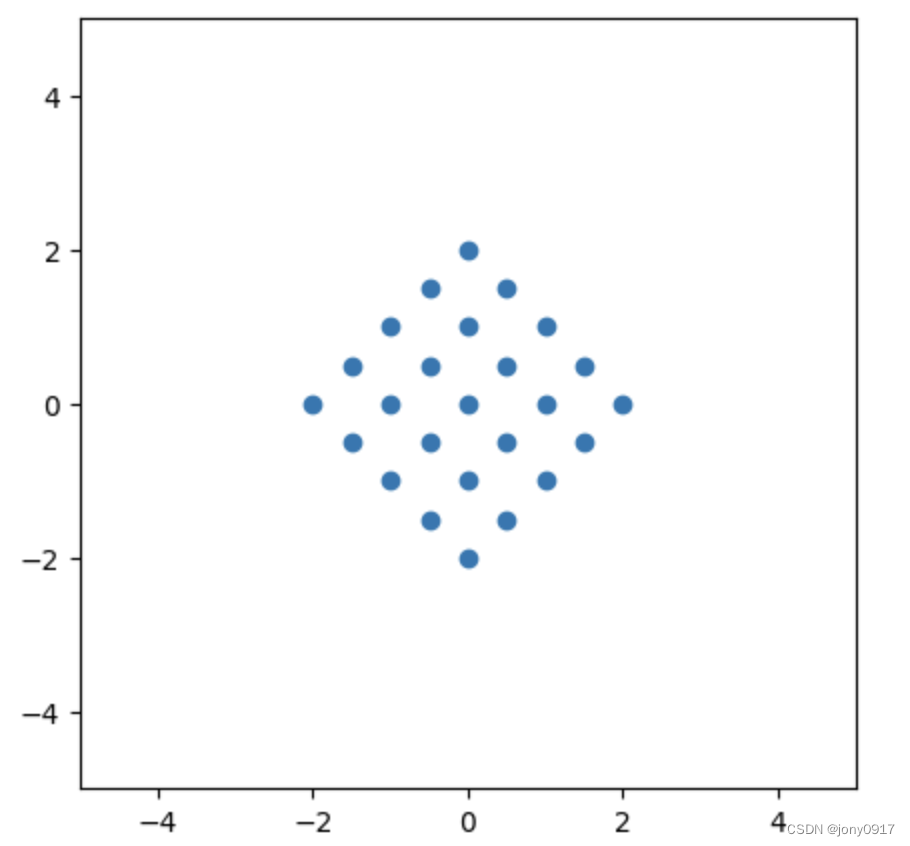 | 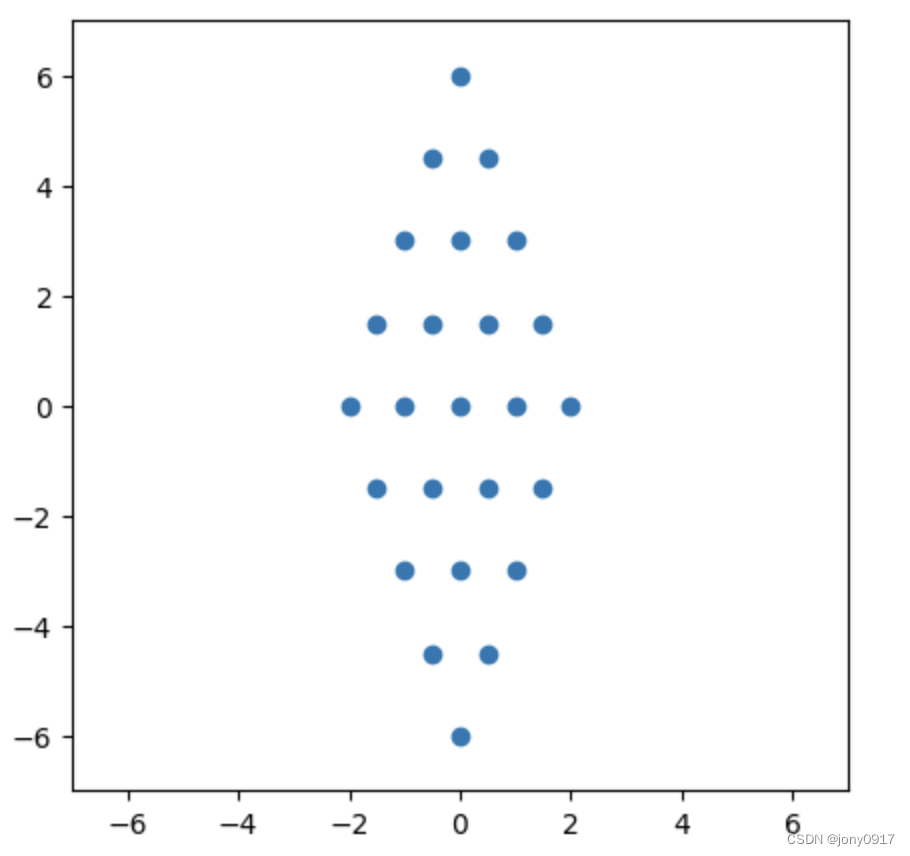 | 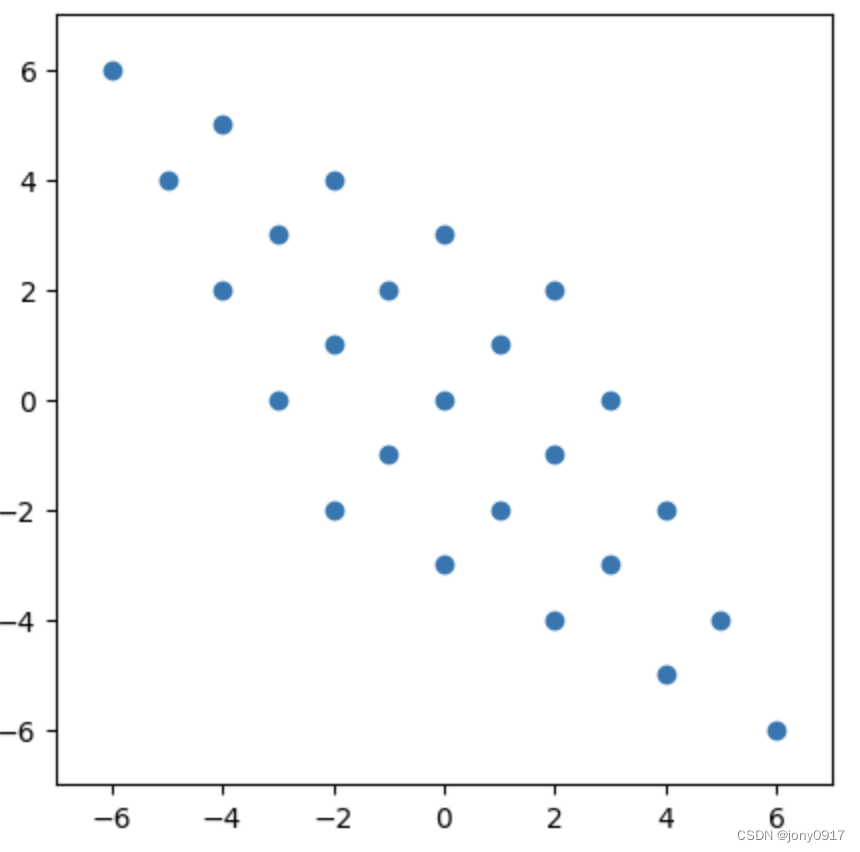 |
奇异值分解(Singular Value Decomposition)
SVD定理:设矩阵 A m × n A^{m\times n} Am×n 的秩为 r ∈ ( 0 , m i n ( m , n ) ) r\in (0, min(m,n)) r∈(0,min(m,n)),矩阵 A 的奇异值分解形式如下
A = U Σ V T A = U\Sigma V^T A=UΣVT
其中 U ∈ R m × m , V ∈ R n × n U\in R^{m\times m},V\in R^{n\times n} U∈Rm×m,V∈Rn×n 是正交矩阵, Σ ∈ R m × n \Sigma\in R^{m\times n} Σ∈Rm×n 满足 Σ i i = σ i ≥ 0 , Σ i j = 0 , i ≠ j \Sigma_{ii} = \sigma_i \ge 0, \Sigma_{ij} = 0, i\ne j Σii=σi≥0,Σij=0,i=j, σ i \sigma_i σi称为奇异值。
图解奇异值分解:
| A = U Σ V T A = U\Sigma V^T A=UΣVT | x | V T x V^Tx VTx | Σ V T x \Sigma V^T x ΣVTx | U Σ V T x U\Sigma V^T x UΣVTx |
|---|---|---|---|---|
|
[
1
1
1
1
0
0
]
=
\begin{bmatrix} 1 & 1 \\ 1 & 1 \\ 0 & 0 \end{bmatrix} =
110110
= [ 1 2 − 1 2 0 1 2 1 2 0 0 0 1 ] [ 2 0 0 0 0 0 ] [ 1 2 − 1 2 1 2 1 2 ] T \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}^T 21210−21210001 200000 [2121−2121]T |  | 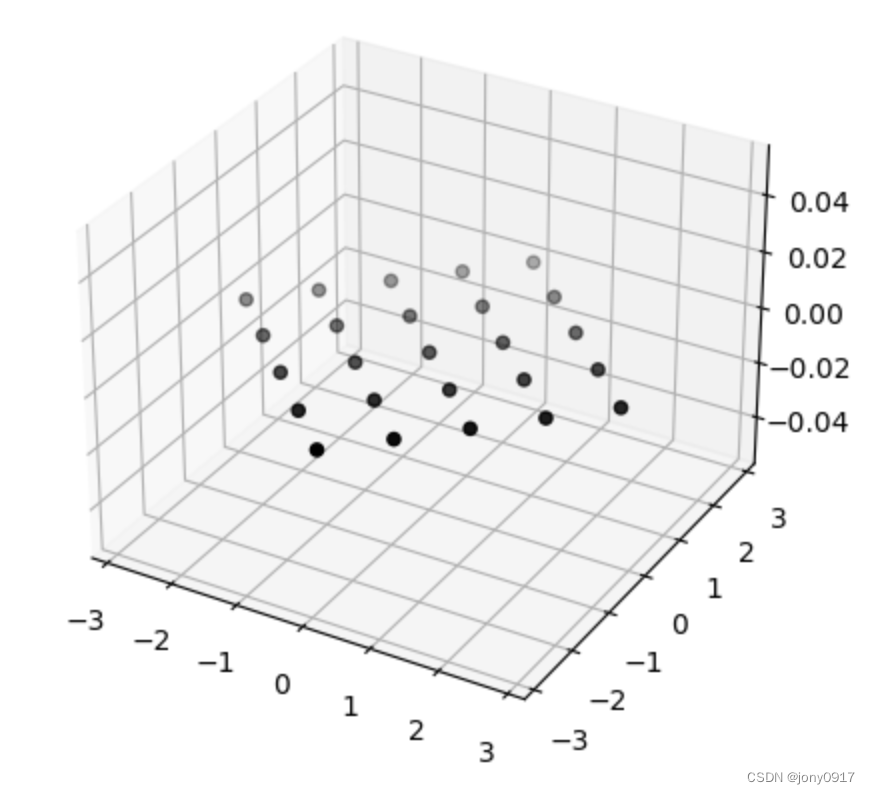 | 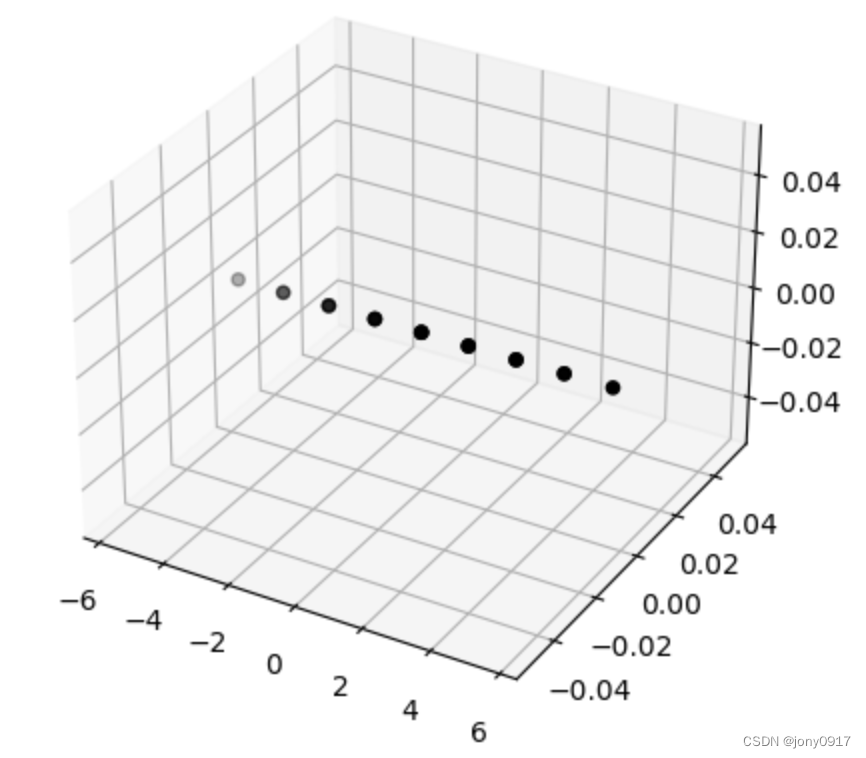 | 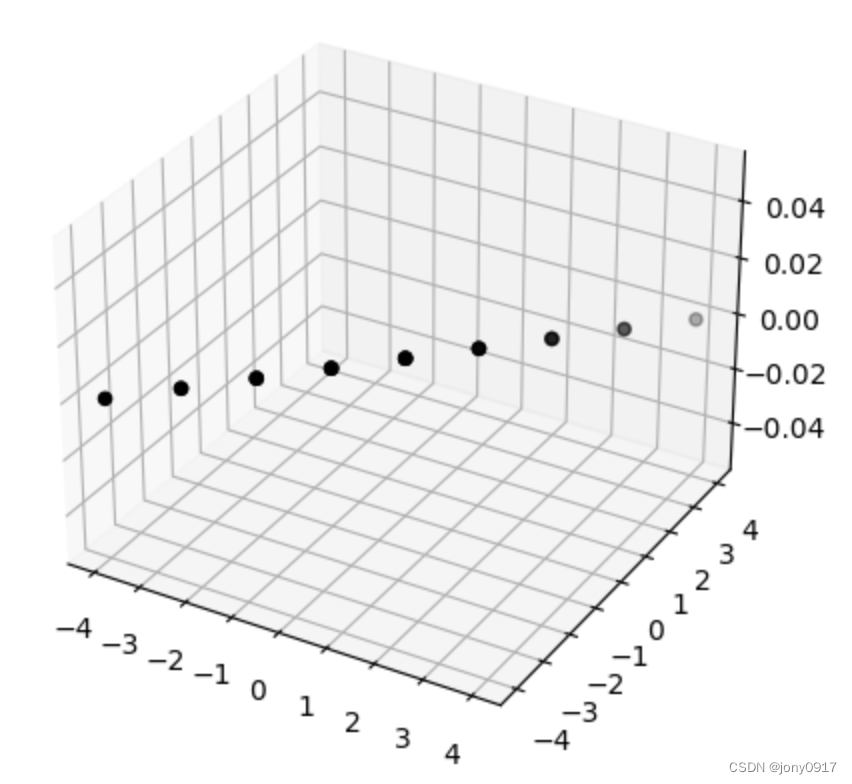 |
|
[
0
1
1
1
1
0
]
=
\begin{bmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{bmatrix} =
011110
= [ 1 6 1 2 1 3 2 6 0 − 1 3 1 6 − 1 2 1 3 ] [ 3 0 0 1 0 0 ] [ 1 2 − 1 2 1 2 1 2 ] T \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}\begin{bmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}^T 616261210−2131−3131 300010 [2121−2121]T |  | 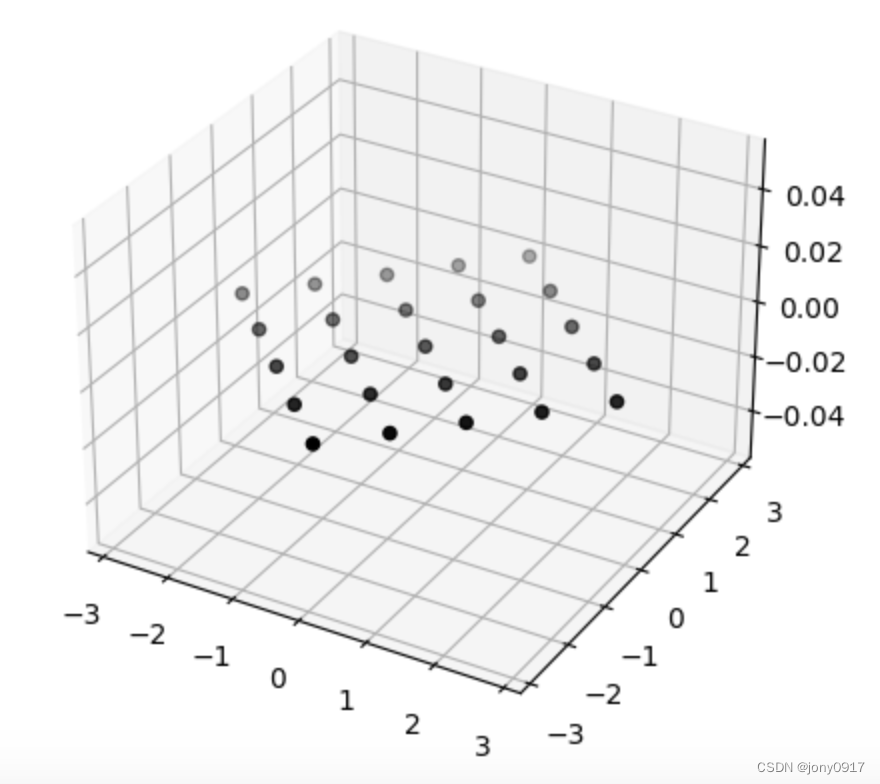 |  |  |