6.1.3 矩阵范数产生向量范数
C n × n C^{n\times n} Cn×n 上任一矩阵范数 ∥ ∙ ∥ \Vert \bullet\Vert ∥∙∥ 都产生一个向量范数 φ ( X ) = ∥ X ∥ V \varphi(X)=\Vert X\Vert_V φ(X)=∥X∥V
- 矩阵范数与向量范数的相容性: φ ( A x ) ≤ ∥ A ∥ φ ( x ) \varphi(Ax)\le \Vert A\Vert\varphi(x) φ(Ax)≤∥A∥φ(x) ,即 ∥ A X ∥ V ≤ ∥ A ∥ ⋅ ∥ X ∥ V \Vert AX\Vert_V\le \Vert A\Vert\cdot\Vert X\Vert_V ∥AX∥V≤∥A∥⋅∥X∥V , ∀ A ∈ C n , n , ∀ X ∈ C n \forall A\in C^{n,n},\forall X\in C^n ∀A∈Cn,n,∀X∈Cn
证明:
设向量范数
φ
(
X
)
=
Δ
∥
X
α
T
∥
,
∀
X
∈
C
n
,
α
=
(
a
1
⋮
a
n
)
≠
0
⃗
为权向量
,
表示对每个列向量放缩形成矩阵
则
φ
(
X
)
=
Δ
∥
X
α
T
∥
=
∥
a
1
X
,
a
2
X
,
⋯
,
a
n
X
∥
,右边为一个矩阵范数
显然①正性:
φ
(
X
)
=
∥
X
α
T
∥
≥
0
②齐性:
φ
(
k
X
)
=
∥
(
k
X
)
α
T
∥
=
∥
a
1
k
X
,
a
2
k
X
,
⋯
,
a
n
k
X
∥
=
∣
k
∣
∥
a
1
X
,
a
2
X
,
⋯
,
a
n
X
n
∥
=
∣
k
∣
φ
(
X
)
③三角性:令
X
,
Y
∈
C
n
,
∵
φ
(
X
+
Y
)
=
∥
(
X
+
Y
)
α
T
∥
=
∥
X
α
T
+
Y
α
T
∥
≤
∥
X
α
T
∥
+
∥
Y
α
T
∥
=
φ
(
X
)
+
φ
(
Y
)
④相容性:
φ
(
A
X
)
=
∥
(
A
X
)
α
T
∥
=
∥
A
(
X
α
T
)
∥
≤
∥
A
∥
⋅
∥
X
α
T
∥
=
∥
A
∥
⋅
φ
(
X
)
可证,
∥
A
X
∥
V
≤
∥
A
∥
⋅
∥
X
∥
V
,
即矩阵范数与向量范数有相容性
\begin{aligned} &设向量范数 \varphi(X)\overset{\Delta}{=}\Vert X\alpha^T\Vert,\forall X\in C^n,\alpha=\left( \begin{matrix} a_1\\\vdots\\a_n \end{matrix} \right)\neq \vec{0}为权向量,表示对每个列向量放缩形成矩阵\\ &则\varphi(X)\overset{\Delta}{=}\Vert X\alpha^T\Vert=\Vert a_1X,a_2X,\cdots,a_nX\Vert,右边为一个矩阵范数\\ &显然 ①正性:\varphi(X)=\Vert X\alpha^T \Vert\ge 0\\ & ②齐性:\varphi(kX)=\Vert (kX)\alpha^T\Vert=\Vert a_1kX,a_2kX,\cdots,a_nkX\Vert=\vert k\vert\Vert a_1X,a_2X,\cdots,a_nX_n\Vert=\vert k\vert\varphi(X)\\ &③三角性:令X,Y\in C^n,\\ &\quad \because \varphi(X+Y)=\Vert (X+Y)\alpha^T\Vert =\Vert X\alpha^T+Y\alpha^T \Vert\le \Vert X\alpha^T\Vert+\Vert Y\alpha^T\Vert =\varphi(X)+\varphi(Y)\\ &④相容性:\varphi(AX)=\Vert (AX)\alpha^T\Vert=\Vert A(X\alpha^T)\Vert\le \Vert A\Vert\cdot\Vert X\alpha^T\Vert=\Vert A\Vert\cdot\varphi(X)\\ &可证,\Vert AX\Vert_V\le \Vert A\Vert\cdot\Vert X\Vert_V,即矩阵范数与向量范数有相容性 \end{aligned}
设向量范数φ(X)=Δ∥XαT∥,∀X∈Cn,α=
a1⋮an
=0为权向量,表示对每个列向量放缩形成矩阵则φ(X)=Δ∥XαT∥=∥a1X,a2X,⋯,anX∥,右边为一个矩阵范数显然①正性:φ(X)=∥XαT∥≥0②齐性:φ(kX)=∥(kX)αT∥=∥a1kX,a2kX,⋯,ankX∥=∣k∣∥a1X,a2X,⋯,anXn∥=∣k∣φ(X)③三角性:令X,Y∈Cn,∵φ(X+Y)=∥(X+Y)αT∥=∥XαT+YαT∥≤∥XαT∥+∥YαT∥=φ(X)+φ(Y)④相容性:φ(AX)=∥(AX)αT∥=∥A(XαT)∥≤∥A∥⋅∥XαT∥=∥A∥⋅φ(X)可证,∥AX∥V≤∥A∥⋅∥X∥V,即矩阵范数与向量范数有相容性
eg
- F范数与向量2-范数相容: ∥ A x ∥ 2 ≤ ∥ A ∥ F ⋅ ∥ x ∥ 2 \Vert Ax\Vert_2\le \Vert A\Vert_F\cdot\Vert x\Vert_2 ∥Ax∥2≤∥A∥F⋅∥x∥2
- 总和范数与1-范数, ∞ \infty ∞-范数相容: ∥ A x ∥ 1 ≤ ∥ A ∥ M ⋅ ∥ x ∥ 1 \Vert Ax\Vert_1\le \Vert A\Vert_M\cdot \Vert x \Vert_1 ∥Ax∥1≤∥A∥M⋅∥x∥1 , ∥ A x ∥ ∞ ≤ ∥ A ∥ M ⋅ ∥ x ∥ ∞ \Vert Ax\Vert_\infty\le \Vert A\Vert_M\cdot \Vert x\Vert_\infty ∥Ax∥∞≤∥A∥M⋅∥x∥∞
- G范数与1-范数, ∞ \infty ∞-范数相容,2-范数相容: ∥ A x ∥ 1 ≤ ∥ A ∥ G ⋅ ∥ x ∥ 1 \Vert Ax\Vert_1\le \Vert A\Vert_G\cdot \Vert x \Vert_1 ∥Ax∥1≤∥A∥G⋅∥x∥1 , ∥ A x ∥ 2 ≤ ∥ A ∥ G ⋅ ∥ x ∥ 2 \Vert Ax\Vert_2\le \Vert A\Vert_G\cdot \Vert x \Vert_2 ∥Ax∥2≤∥A∥G⋅∥x∥2 , ∥ A x ∥ ∞ ≤ ∥ A ∥ G ⋅ ∥ x ∥ ∞ \Vert Ax\Vert_\infty\le \Vert A\Vert_G\cdot \Vert x \Vert_\infty ∥Ax∥∞≤∥A∥G⋅∥x∥∞
a. 特别生成公式
令 e 1 = ( 1 0 ⋮ 0 ) e_1=\left(\begin{matrix}1\\0\\\vdots\\0\end{matrix}\right) e1= 10⋮0 ,取 e 1 T e^T_1 e1T 作为向量 X X X 的放缩量,将向量范数与矩阵范数建立联系
φ ( X ) = Δ ∥ X e 1 T ∥ V = ∥ X ( 1 , 0 , ⋯ , 0 ) ∥ = ∥ ( x 1 0 ⋯ 0 x 2 0 ⋯ 0 ⋮ ⋮ ⋱ ⋮ x n 0 ⋯ 0 ) ∥ ∗ \varphi(X)\overset{\Delta}{=}\Vert Xe_1^T\Vert_V=\Vert X(1,0,\cdots,0)\Vert=\left\Vert \left(\begin{matrix} x_1&0&\cdots&0\\x_2&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\x_n&0&\cdots&0\end{matrix}\right)\right\Vert_* φ(X)=Δ∥Xe1T∥V=∥X(1,0,⋯,0)∥= x1x2⋮xn00⋮0⋯⋯⋱⋯00⋮0 ∗ , X = ( x 1 ⋮ x n ) ∈ C n X =\left(\begin{matrix}x_1\\\vdots\\x_n\end{matrix}\right)\in C^n X= x1⋮xn ∈Cn ,且 ∥ X ∥ V \Vert X\Vert_V ∥X∥V 满足相容性 ∥ A X ∥ V ≤ ∥ A ∥ ∗ ⋅ ∥ X ∥ V \Vert AX\Vert_V\le \Vert A\Vert_*\cdot\Vert X\Vert_{V} ∥AX∥V≤∥A∥∗⋅∥X∥V , A ∈ C n , n A\in C^{n,n} A∈Cn,n , X ∈ C n X\in C^n X∈Cn
eg
取 F 范数
∥
A
∥
=
∥
A
∥
F
\Vert A\Vert=\Vert A\Vert_F
∥A∥=∥A∥F ,验证F范数与向量2-范数的相容性
由特别生成公式,
∥
X
∥
V
=
Δ
∥
X
e
1
T
∥
=
∥
(
x
1
0
⋯
0
x
2
0
⋯
0
⋮
⋮
⋱
⋮
x
n
0
⋯
0
)
∥
F
=
∣
x
1
∣
2
+
∣
x
2
∣
2
+
⋯
+
∣
x
n
∣
2
=
∥
X
∥
2
,
即有
F
范数
∥
A
∥
F
可产生向量范数
∥
X
∥
2
对相容性的验证:
∀
A
∈
C
n
,
n
,
∥
A
X
∥
2
=
∥
(
A
X
)
e
1
T
∥
=
∥
A
(
X
e
1
T
)
∥
≤
∥
A
∥
F
⋅
∥
X
∥
2
\begin{aligned} &由特别生成公式,\Vert X\Vert_V\overset{\Delta}{=}\Vert Xe_1^T\Vert=\left\Vert \left(\begin{matrix} x_1&0&\cdots&0\\x_2&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\x_n&0&\cdots&0\end{matrix}\right)\right\Vert_F = \sqrt{\vert x_1\vert^2+\vert x_2\vert^2+\cdots+\vert x_n\vert^2}\\ &=\Vert X\Vert_2,即有F范数\Vert A\Vert_F可产生向量范数 \Vert X\Vert_2\\ &对相容性的验证:\\ &\forall A\in C^{n,n},\Vert AX\Vert_2=\Vert (AX)e_1^T\Vert=\Vert A(Xe_1^T)\Vert\le \Vert A\Vert_F\cdot \Vert X\Vert_2 \end{aligned}
由特别生成公式,∥X∥V=Δ∥Xe1T∥=
x1x2⋮xn00⋮0⋯⋯⋱⋯00⋮0
F=∣x1∣2+∣x2∣2+⋯+∣xn∣2=∥X∥2,即有F范数∥A∥F可产生向量范数∥X∥2对相容性的验证:∀A∈Cn,n,∥AX∥2=∥(AX)e1T∥=∥A(Xe1T)∥≤∥A∥F⋅∥X∥2
取总和范数
∥
A
∥
M
=
∑
∣
a
i
j
∣
\Vert A\Vert_M=\sum \vert a_{ij}\vert
∥A∥M=∑∣aij∣ ,写出矩阵范数产生的向量范数,并写出相容性
由特别生成公式
,
∥
X
∥
V
=
Δ
∥
X
e
1
T
∥
=
∥
(
x
1
0
⋯
0
x
2
0
⋯
0
⋮
⋮
⋱
⋮
x
n
0
⋯
0
)
∥
M
=
∑
∣
a
i
j
∣
=
∥
X
∥
1
即有相容性:
∥
A
X
∥
1
=
∥
A
X
e
1
T
∥
≤
∥
A
∥
⋅
∥
X
∥
1
=
∥
A
∥
M
⋅
∥
X
∥
1
至于
M
范数与
∞
−
范数相容,则需要其他的生成公式证明
\begin{aligned} &由特别生成公式,\Vert X\Vert_V\overset{\Delta}{=}\Vert Xe_1^T\Vert=\left\Vert \left(\begin{matrix} x_1&0&\cdots&0\\x_2&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\x_n&0&\cdots&0\end{matrix}\right)\right\Vert_M=\sum \vert a_{ij}\vert =\Vert X\Vert_1\\ &即有相容性:\Vert AX\Vert_1=\Vert AXe_1^T\Vert\le \Vert A\Vert\cdot\Vert X\Vert_1=\Vert A\Vert_M\cdot \Vert X\Vert_1\\ &至于M范数与\infty-范数相容,则需要其他的生成公式证明 \end{aligned}
由特别生成公式,∥X∥V=Δ∥Xe1T∥=
x1x2⋮xn00⋮0⋯⋯⋱⋯00⋮0
M=∑∣aij∣=∥X∥1即有相容性:∥AX∥1=∥AXe1T∥≤∥A∥⋅∥X∥1=∥A∥M⋅∥X∥1至于M范数与∞−范数相容,则需要其他的生成公式证明
取行范数
∥
A
∥
∞
\Vert A\Vert_\infty
∥A∥∞ ,写出矩阵范数产生的向量范数,并写出相容性
由特别生成公式,
∥
X
∥
V
=
Δ
∥
X
e
1
T
∥
=
∥
(
x
1
0
⋯
0
x
2
0
⋯
0
⋮
⋮
⋱
⋮
x
n
0
⋯
0
)
∥
∞
=
max
1
≤
i
≤
n
{
∣
x
i
∣
}
=
∥
X
∥
∞
∥
A
X
∥
∞
≤
∥
A
∥
∞
∥
X
∥
∞
\begin{aligned} &由特别生成公式,\Vert X\Vert_V\overset{\Delta}{=}\Vert Xe_1^T\Vert=\left\Vert \left(\begin{matrix} x_1&0&\cdots&0\\x_2&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\x_n&0&\cdots&0\end{matrix}\right)\right\Vert_\infty=\max_{1\le i\le n}\{\vert x_i\vert\}=\Vert X\Vert_{\infty}\\ &\Vert AX\Vert_\infty\le\Vert A\Vert_\infty\Vert X\Vert_\infty \end{aligned}
由特别生成公式,∥X∥V=Δ∥Xe1T∥=
x1x2⋮xn00⋮0⋯⋯⋱⋯00⋮0
∞=1≤i≤nmax{∣xi∣}=∥X∥∞∥AX∥∞≤∥A∥∞∥X∥∞
取列范数 ∥ A ∥ 1 \Vert A\Vert_1 ∥A∥1 ,由特别生成公式 ∥ X ∥ V = Δ ∥ X ∥ 1 \Vert X\Vert_V\overset{\Delta}{=}\Vert X \Vert_1 ∥X∥V=Δ∥X∥1 , ∥ A X ∥ 1 ≤ ∥ A ∥ 1 ⋅ ∥ X ∥ 1 \Vert AX\Vert_1 \le \Vert A\Vert_1 \cdot \Vert X \Vert_1 ∥AX∥1≤∥A∥1⋅∥X∥1
6.1.4 谱范不等式
a. 谱半径
ρ ( A ) = m a x { ∣ λ 1 ∣ , ∣ λ 2 ∣ , ⋯ , ∣ λ n ∣ } 为方阵 A = A n × n 的谱半径, 其中,方阵 A 的特征根为 λ ( A ) = { λ 1 , ⋯ , λ n } \begin{aligned} &\rho(A)=max\{\vert \lambda_1\vert,\vert \lambda_2\vert,\cdots,\vert \lambda_n\vert\}为方阵 A=A_{n\times n} 的谱半径,\\ &其中,方阵A的特征根为\lambda(A)=\{\lambda_1,\cdots,\lambda_n\} \end{aligned} ρ(A)=max{∣λ1∣,∣λ2∣,⋯,∣λn∣}为方阵A=An×n的谱半径,其中,方阵A的特征根为λ(A)={λ1,⋯,λn}
eg
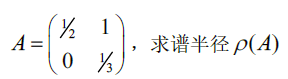
∵ λ 1 = 1 2 , λ 2 = 1 3 , ∴ ρ ( A ) = λ 1 = 1 2 \begin{aligned} &\because \lambda_1=\frac{1}{2},\lambda_2=\frac{1}{3},\therefore \rho(A)=\lambda_1=\frac{1}{2} \end{aligned} ∵λ1=21,λ2=31,∴ρ(A)=λ1=21
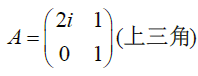
λ ( A ) = { 2 i , 1 } , ρ ( A ) = 2 \begin{aligned} &\lambda(A)=\{2i,1\},\rho(A)=2 \end{aligned} λ(A)={2i,1},ρ(A)=2
a. 谱半径性质
-
正性:任一方阵 A n × n A_{n\times n} An×n 必有 ρ ( A ) ≥ 0 \rho(A)\ge 0 ρ(A)≥0
-
齐次公式: ρ ( k A ) = ∣ k ∣ ρ ( A ) \rho(kA)=\vert k\vert \rho(A) ρ(kA)=∣k∣ρ(A)
可写齐次公式 ρ ( A k ) = 1 ∣ k ∣ ρ ( A ) \rho(\frac{A}{k})=\frac{1}{\vert k\vert}\rho(A) ρ(kA)=∣k∣1ρ(A)
可取正数 k = ρ ( A ) + ϵ , ϵ > 0 k=\rho(A)+\epsilon,\epsilon>0 k=ρ(A)+ϵ,ϵ>0 ,则有 ρ ( A k ) = ρ ( A ρ ( A ) + ϵ ) = 1 ρ ( A ) + ϵ ρ ( A ) < 1 \rho(\frac{A}{k})=\rho(\frac{A}{\rho(A)+\epsilon})=\frac{1}{\rho(A)+\epsilon}\rho(A)<1 ρ(kA)=ρ(ρ(A)+ϵA)=ρ(A)+ϵ1ρ(A)<1
-
幂公式: ρ ( A k ) = [ ρ ( A ) ] k \rho(A^k)=[\rho(A)]^k ρ(Ak)=[ρ(A)]k
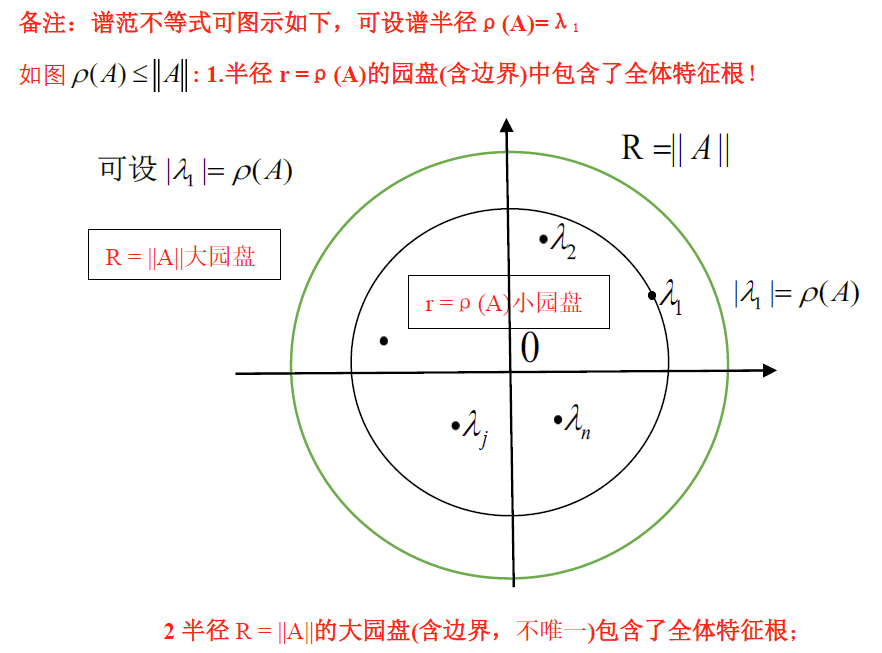
b. 谱范不等式
ρ ( A ) ≤ ∥ A ∥ \rho(A)\le \Vert A\Vert ρ(A)≤∥A∥ 对于一切矩阵范数 ∥ A ∥ \Vert A\Vert ∥A∥ 成立
- SP:若 A 是正规阵,则 ρ ( A ) = ∥ A ∥ 2 \rho(A)=\Vert A\Vert_2 ρ(A)=∥A∥2
- ρ ( A ) = lim k → ∞ ∥ A k ∥ 1 k \rho(A)=\lim_{k\rightarrow \infty}\limits\Vert A^k\Vert^{\frac{1}{k}} ρ(A)=k→∞lim∥Ak∥k1
证明:
λ
(
A
)
=
{
λ
1
,
λ
2
,
⋯
,
λ
n
}
,
λ
1
=
m
a
x
{
∣
λ
1
∣
,
⋯
,
∣
λ
n
∣
}
=
ρ
(
A
)
取特根
X
≠
0
,
使
A
X
=
λ
1
X
,
令矩阵
B
=
(
X
,
X
,
⋯
,
X
)
n
×
n
≠
0
可知
A
B
=
(
A
X
,
⋯
,
A
X
)
=
λ
1
B
,
∣
λ
1
∣
∥
B
∥
=
∥
A
B
∥
≤
∥
A
∥
⋅
∥
B
∥
,且
∥
B
∥
>
0
∴
∣
λ
1
∣
<
∥
A
∥
,
由谱半径定义得:
ρ
(
A
)
=
∥
A
∥
\begin{aligned} &\lambda(A)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\} ,\lambda_1=max\{\vert\lambda_1\vert,\cdots,\vert \lambda_n\vert\} =\rho(A)\\ &取特根X\neq 0,使AX=\lambda_1X,令矩阵B=\left(X,X,\cdots,X\right)_{n\times n}\neq 0\\ &可知AB=(AX,\cdots,AX)=\lambda_1B,\vert \lambda_1\vert\Vert B\Vert=\Vert AB\Vert\le \Vert A\Vert\cdot\Vert B\Vert,且\Vert B\Vert>0\\ &\therefore \vert \lambda_1\vert<\Vert A\Vert,由谱半径定义得:\rho(A)=\Vert A\Vert \end{aligned}
λ(A)={λ1,λ2,⋯,λn},λ1=max{∣λ1∣,⋯,∣λn∣}=ρ(A)取特根X=0,使AX=λ1X,令矩阵B=(X,X,⋯,X)n×n=0可知AB=(AX,⋯,AX)=λ1B,∣λ1∣∥B∥=∥AB∥≤∥A∥⋅∥B∥,且∥B∥>0∴∣λ1∣<∥A∥,由谱半径定义得:ρ(A)=∥A∥
证明2:
任取矩阵范数
∥
A
∥
,
产生向量范数
∥
X
∥
,
且
∥
A
X
∥
≤
∣
A
∥
⋅
∥
X
∥
任取
A
的特征值
λ
,
有特向
X
≠
0
,
使
A
X
=
λ
X
则
∣
λ
∣
∥
X
∥
=
∥
λ
X
∥
=
∥
A
X
∥
≤
∥
A
∥
⋅
∥
X
∥
,
且
∥
X
∥
>
0
∴
∣
λ
∣
≤
∥
A
∥
⇒
ρ
(
A
)
≤
∥
A
∥
\begin{aligned} &任取矩阵范数 \Vert A\Vert,产生向量范数\Vert X\Vert,且 \Vert AX\Vert\le \vert A\Vert\cdot\Vert X\Vert\\ &任取A的特征值\lambda,有特向X\neq 0,使 AX=\lambda X\\ &则\vert \lambda\vert\Vert X\Vert=\Vert \lambda X\Vert=\Vert AX\Vert\le \Vert A\Vert\cdot \Vert X\Vert,且 \Vert X\Vert>0\\ &\therefore \vert \lambda\vert\le \Vert A\Vert\Rightarrow \rho(A)\le \Vert A\Vert \end{aligned}
任取矩阵范数∥A∥,产生向量范数∥X∥,且∥AX∥≤∣A∥⋅∥X∥任取A的特征值λ,有特向X=0,使AX=λX则∣λ∣∥X∥=∥λX∥=∥AX∥≤∥A∥⋅∥X∥,且∥X∥>0∴∣λ∣≤∥A∥⇒ρ(A)≤∥A∥
c. 小范数定理
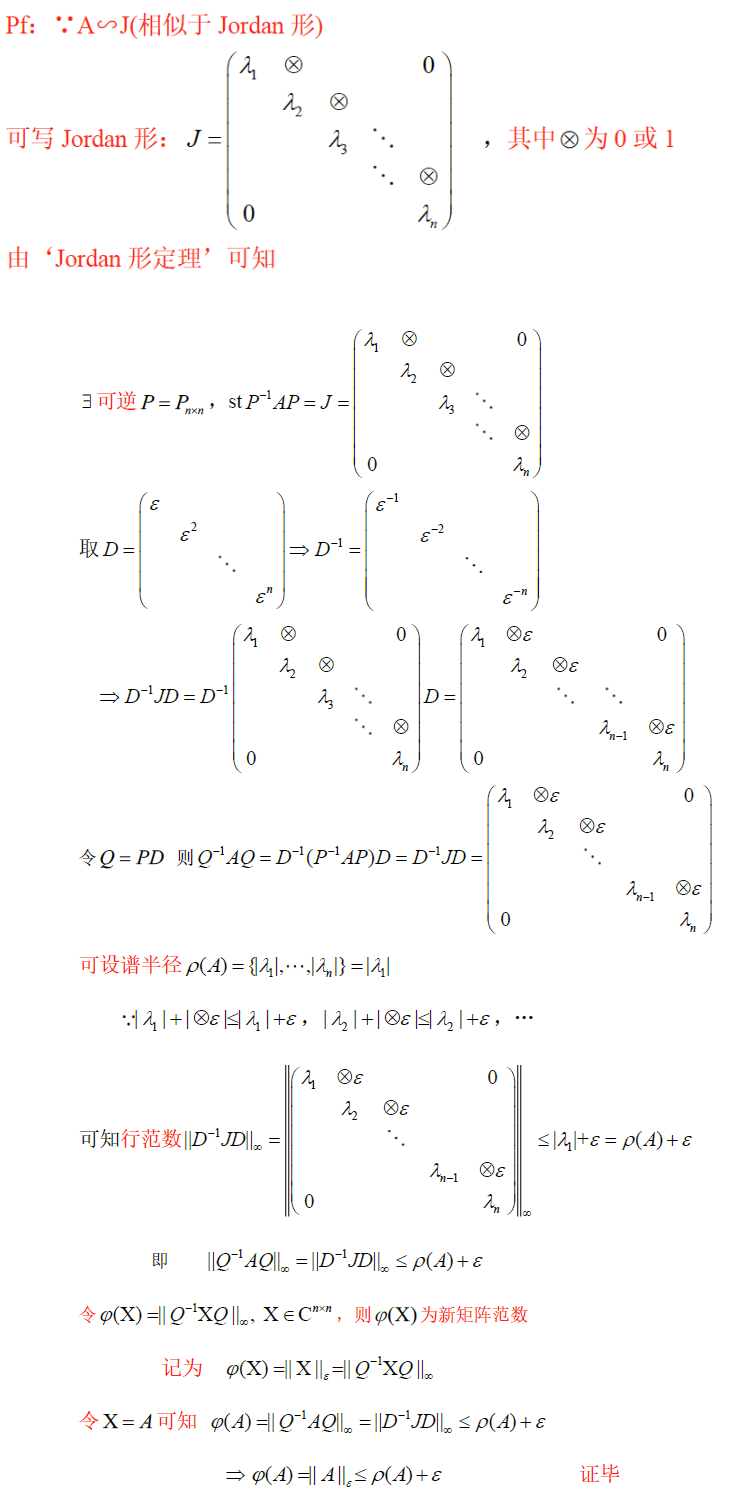
设 A ∈ C n , n A\in C^{n,n} A∈Cn,n 固定,任取很小正数 ϵ > 0 \epsilon>0 ϵ>0 ,则有矩阵范数 ∥ ∙ ∥ ϵ \Vert \bullet\Vert_\epsilon ∥∙∥ϵ ,使 ∥ A ∥ ϵ ≤ ρ ( A ) + ϵ \Vert A\Vert_\epsilon\le \rho(A)+\epsilon ∥A∥ϵ≤ρ(A)+ϵ
证明小范数定理
新范数公式:固定可逆阵 P = P n × n P=P_{n\times n} P=Pn×n , ∥ A ∥ \Vert A\Vert ∥A∥ 为矩阵范数 A ∈ C n × n A\in C^{n\times n} A∈Cn×n ,令 φ ( A ) = ∥ P − 1 A P ∥ \varphi(A)=\Vert P^{-1}AP\Vert φ(A)=∥P−1AP∥ ,则 φ ( A ) \varphi(A) φ(A) 为矩阵范数,记新范数为 φ ( A ) = ∥ A ∥ P \varphi(A)=\Vert A\Vert_P φ(A)=∥A∥P 或 $\varphi(A)=\Vert A\Vert_新 $


推论
若
ρ
(
A
)
<
1
\rho(A)<1
ρ(A)<1 ,则有某个范数
∥
A
∥
ϵ
<
1
\Vert A\Vert_\epsilon<1
∥A∥ϵ<1
∵
ρ
(
A
)
<
1
,则
1
−
ρ
(
A
)
>
0
,
取
ϵ
>
0
很小,任意
ϵ
<
1
2
[
1
−
ρ
(
A
)
]
可知
ρ
(
A
)
+
ϵ
<
ρ
(
A
)
+
1
2
[
1
−
ρ
(
A
)
]
=
1
2
[
1
+
ρ
(
A
)
]
<
1
,
由小范数定理,
∃
∥
A
∥
ϵ
<
ρ
(
A
)
+
ϵ
<
1
\begin{aligned} &\because \rho(A)<1,则1-\rho(A)>0,取\epsilon>0很小,任意\epsilon <\frac{1}{2}[1-\rho(A)]\\ &可知 \rho(A)+\epsilon<\rho(A)+\frac{1}{2}[1-\rho(A)] = \frac{1}{2}[1+\rho(A)]<1,\\ &由小范数定理,\exist\Vert A\Vert_\epsilon<\rho(A)+\epsilon<1 \end{aligned}
∵ρ(A)<1,则1−ρ(A)>0,取ϵ>0很小,任意ϵ<21[1−ρ(A)]可知ρ(A)+ϵ<ρ(A)+21[1−ρ(A)]=21[1+ρ(A)]<1,由小范数定理,∃∥A∥ϵ<ρ(A)+ϵ<1
总结
给定方阵 A n × n A_{n\times n} An×n , ∀ ϵ > 0 \forall \epsilon >0 ∀ϵ>0 ,有某个范数 ∥ ∙ ∥ ϵ < ρ ( A ) + ϵ \Vert \bullet\Vert_\epsilon<\rho(A)+\epsilon ∥∙∥ϵ<ρ(A)+ϵ
SP:若 ρ ( A ) < 1 \rho(A)<1 ρ(A)<1 ,则有某范数 ∥ A ∥ ϵ < 1 \Vert A\Vert_\epsilon<1 ∥A∥ϵ<1
若 A = A n × n A=A_{n\times n} A=An×n 为单阵(相似与对角阵) ,则存在矩阵范数 ∥ X ∥ P , X ∈ C n × n \Vert X\Vert_P,X\in C^{n\times n} ∥X∥P,X∈Cn×n ,使得 $\Vert A\Vert_P=\rho(A) $
e. 谱范的应用——矩阵绝对收敛判定
若方阵A满足 A k → 0 ( k → ∞ ) A^k\rightarrow 0(k\rightarrow \infty) Ak→0(k→∞) ,即 lim k → ∞ A k = 0 \lim_{k\rightarrow\infty}\limits A^k=0 k→∞limAk=0 ,称A为收敛阵
充要条件
-
lim k → ∞ A k = 0 ⟺ ∥ A k ∥ = 0 \lim_{k\rightarrow\infty}\limits A^k=0\iff \Vert A^k\Vert=0 k→∞limAk=0⟺∥Ak∥=0
证明:
∵ lim k → ∞ A k = 0 ⟺ A k 中每个元素 a i j ( k ) → 0 ⟺ ∥ A k ∥ M = ∑ i , j ∣ a i j ( k ) ∣ → k → ∞ 0 且由矩阵范数等价性,有 lim k → ∞ A k = 0 ⟺ ∥ A k ∥ → k → ∞ 0 \begin{aligned} &\because \lim_{k\rightarrow \infty}A^k=0\iff A^k中每个元素 a_{ij}^{(k)}\rightarrow 0\iff \Vert A^k\Vert_M=\sum_{i,j}\vert a_{ij}^{(k)}\vert\xrightarrow{k\rightarrow \infty} 0\\ &且 由矩阵范数等价性,有\lim_{k\rightarrow \infty}\limits A^k=0\iff \Vert A^k\Vert\xrightarrow{k\rightarrow \infty}0 \end{aligned} ∵k→∞limAk=0⟺Ak中每个元素aij(k)→0⟺∥Ak∥M=i,j∑∣aij(k)∣k→∞0且由矩阵范数等价性,有k→∞limAk=0⟺∥Ak∥k→∞0 -
ρ ( A ) < 1 ⟺ ∥ A k ∥ → 0 ( k → ∞ ) ⇒ A k → 0 ( k → ∞ ) \rho(A)<1\iff \Vert A^k\Vert\rightarrow 0 (k\rightarrow \infty)\Rightarrow A^k\rightarrow 0(k\rightarrow \infty) ρ(A)<1⟺∥Ak∥→0(k→∞)⇒Ak→0(k→∞)
-
充分性:
若 ρ ( A ) < 1 \rho(A)<1 ρ(A)<1,则 ∃ \exist ∃ 某小范数 ∥ A ∥ ϵ < 1 ⇒ ∥ A k ∥ ϵ ≤ ∥ A ∥ ϵ k → 0 ⟺ ∥ A k ∥ ϵ → 0 \Vert A\Vert_\epsilon<1\Rightarrow \Vert A^k\Vert_\epsilon\le \Vert A\Vert^k_\epsilon\rightarrow 0\iff \Vert A^k\Vert_\epsilon\rightarrow 0 ∥A∥ϵ<1⇒∥Ak∥ϵ≤∥A∥ϵk→0⟺∥Ak∥ϵ→0
由于范数等价性,对于所有范数都有 ∥ A k ∥ → k → ∞ 0 \Vert A^k\Vert\xrightarrow{k\rightarrow \infty}0 ∥Ak∥k→∞0
-
必要性:
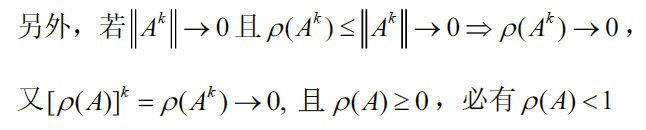
-
充分条件
-
某一范数 ∥ A ∥ < 1 ⇒ ∥ A k ∥ → 0 ( k → ∞ ) \Vert A\Vert<1\Rightarrow \Vert A^k\Vert\rightarrow 0(k\rightarrow \infty) ∥A∥<1⇒∥Ak∥→0(k→∞)
若范数 ∥ A ∥ < 1 ⇒ ∥ A k ∥ ≤ ∥ A ∥ k \Vert A\Vert<1\Rightarrow \Vert A^k\Vert\le \Vert A\Vert^k ∥A∥<1⇒∥Ak∥≤∥A∥k 已知 ∥ A ∥ < 1 ⇒ ∥ A ∥ k → k → ∞ 0 \Vert A\Vert<1\Rightarrow \Vert A\Vert^k\xrightarrow{k\rightarrow \infty} 0 ∥A∥<1⇒∥A∥kk→∞0 ,则 ⇒ ∥ A k ∥ → 0 ⇒ A k → k → ∞ 0 , A 为收敛阵 \Rightarrow \Vert A^k\Vert\rightarrow 0\Rightarrow A^k\xrightarrow{k\rightarrow\infty} 0,A为收敛阵 ⇒∥Ak∥→0⇒Akk→∞0,A为收敛阵
总结
ρ ( A ) < 1 ⟺ A k → 0 ( k → ∞ ) \rho(A)<1\iff A^k\rightarrow 0(k\rightarrow \infty) ρ(A)<1⟺Ak→0(k→∞) ,A为收敛阵
某一范数 ∥ A ∥ < 1 ⇒ A k → 0 ( k → ∞ ) \Vert A\Vert<1\Rightarrow A^k\rightarrow 0(k\rightarrow \infty) ∥A∥<1⇒Ak→0(k→∞) ,A为收敛阵
纽曼公式(矩阵级数收敛公式)
-
若 ρ ( A ) < 1 \rho(A)<1 ρ(A)<1 ,则 I + A + A 2 + ⋯ + A k = ( I − A ) − 1 I+A+A^2+\cdots+A^k=(I-A)^{-1} I+A+A2+⋯+Ak=(I−A)−1 ;
若 ρ ( A ) ≥ 1 \rho(A)\ge 1 ρ(A)≥1 ,则 I + A + A 2 + ⋯ + A k I+A+A^2+\cdots+A^k I+A+A2+⋯+Ak 发散,无意义
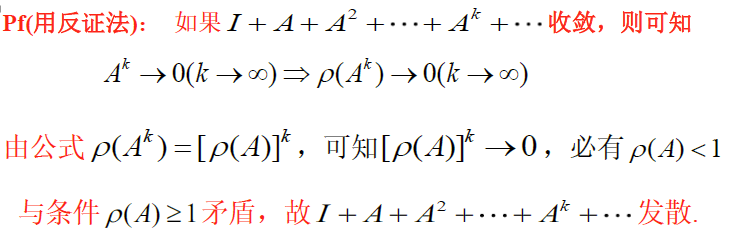
-
若某范数 ∥ A ∥ < 1 \Vert A\Vert<1 ∥A∥<1 ,则 I + A + A 2 + ⋯ + A k = ( I − A ) − 1 I+A+A^2+\cdots+A^k=(I-A)^{-1} I+A+A2+⋯+Ak=(I−A)−1
证明
(
1
)
已知
ρ
(
A
)
<
1
⇒
A
k
→
0
(
k
→
∞
)
(
I
−
A
)
(
I
+
A
+
A
2
+
⋯
+
A
k
)
=
I
−
A
k
+
1
当
k
→
∞
,
⇒
(
I
−
A
)
(
I
+
A
+
A
2
+
⋯
+
A
k
)
=
I
故可得
(
I
−
A
)
−
1
=
I
+
A
+
A
2
+
⋯
+
A
k
\begin{aligned} &(1)已知\rho(A)<1\Rightarrow A^k\rightarrow 0(k\rightarrow \infty) \\ &(I-A)(I+A+A^2+\cdots+A^k)=I-A^{k+1}\\ &当k\rightarrow \infty,\Rightarrow (I-A)(I+A+A^2+\cdots+A^k)=I\\ &故可得 (I-A)^{-1}=I+A+A^2+\cdots+A^k \end{aligned}
(1)已知ρ(A)<1⇒Ak→0(k→∞)(I−A)(I+A+A2+⋯+Ak)=I−Ak+1当k→∞,⇒(I−A)(I+A+A2+⋯+Ak)=I故可得(I−A)−1=I+A+A2+⋯+Ak
( 2 ) 若 ∥ A ∥ < 1 , 则 ρ ( A ) ≤ ∥ A ∥ < 1 , 由 ( 1 ) 结论,可知结论成立 \begin{aligned} &(2)若 \Vert A\Vert<1,则\rho(A)\le \Vert A\Vert <1,由(1)结论,可知结论成立 \end{aligned} (2)若∥A∥<1,则ρ(A)≤∥A∥<1,由(1)结论,可知结论成立
eg
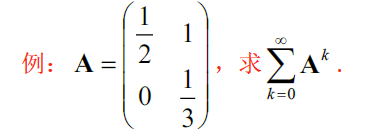
∥ A ∥ 1 = 4 3 , ∥ A ∥ ∞ = 3 2 , λ ( A ) = { 1 2 , 1 3 } , ρ ( A ) < 1 故 ∑ k = 0 ∞ A k = ( I − A ) − 1 = ( 1 2 − 1 0 2 3 ) − 1 = 3 ( 2 3 1 0 1 2 ) = ( 2 3 0 3 2 ) \begin{aligned} &\Vert A\Vert_1=\frac{4}{3},\Vert A\Vert_\infty=\frac{3}{2},\lambda(A)=\{\frac{1}{2},\frac{1}{3}\} ,\rho(A)<1\\ &故\sum_{k=0}\limits^\infty A^k=(I-A)^{-1}=\left( \begin{matrix} \frac{1}{2}&-1\\0&\frac{2}{3} \end{matrix} \right)^{-1}=3\left( \begin{matrix} \frac{2}{3}&1\\0&\frac{1}{2} \end{matrix} \right)=\left( \begin{matrix} 2&3\\0&\frac{3}{2} \end{matrix} \right) \end{aligned} ∥A∥1=34,∥A∥∞=23,λ(A)={21,31},ρ(A)<1故k=0∑∞Ak=(I−A)−1=(210−132)−1=3(320121)=(20323)
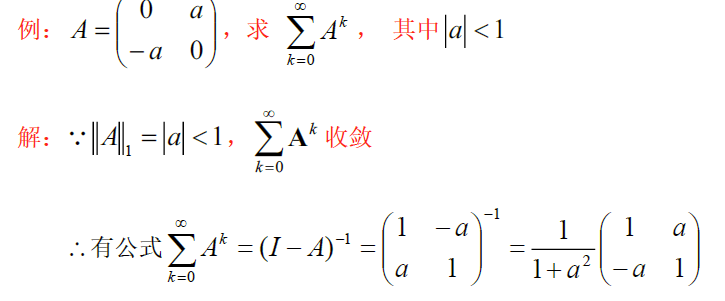
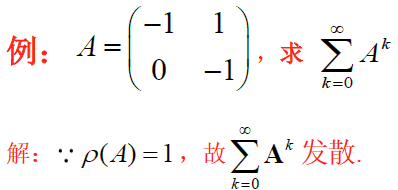
∥ ( I − A ) − 1 ∥ \Vert (I-A)^{-1}\Vert ∥(I−A)−1∥ 计算
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n , ∥ A ∥ \Vert A\Vert ∥A∥ 是矩阵范数,若 ∥ A ∥ < 1 \Vert A\Vert<1 ∥A∥<1 ,则 I − A I-A I−A 为非奇异阵(可逆),且 ∥ ( I − A ) − 1 ∥ ≤ ∥ I ∥ 1 − ∥ A ∥ \Vert (I-A)^{-1}\Vert\le \frac{\Vert I\Vert}{1-\Vert A\Vert} ∥(I−A)−1∥≤1−∥A∥∥I∥