想要精通算法和SQL的成长之路 - 验证二叉树
- 前言
- 一. 验证二叉树
- 1.1 并查集
- 1.2 入度以及边数检查
前言
想要精通算法和SQL的成长之路 - 系列导航
并查集的运用
一. 验证二叉树
原题链接
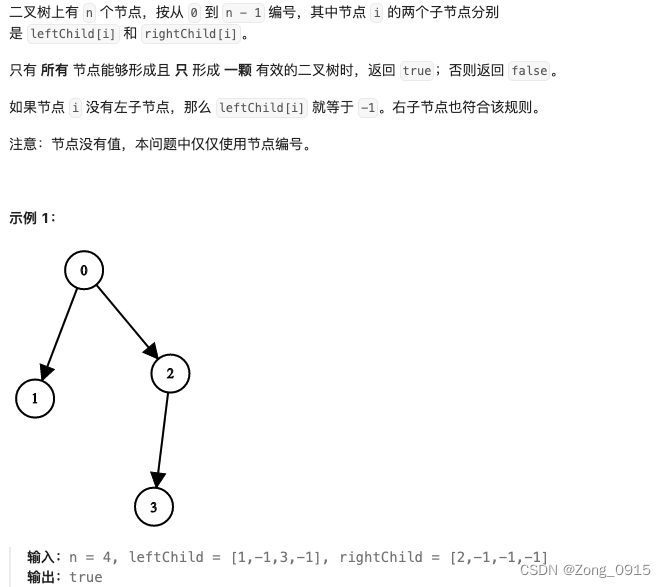
思路如下:
-
对于一颗二叉树,我们需要做哪些校验?
-
首先这颗树不可以成环,如图:

-
其次,这颗树的边数量,应该等于 n -1。如下图就是错的:

-
存在一个根节点,它的入度为0,其他所有的节点,入度都不能够超过1。
那么针对以上几点,我们可以分别来考虑。我们同时遍历一次左右节点数组。值不是-1的话,说明该端连接的节点非空。
- 我们用一个
int[] inDegree数组代表入度。对应值非-1的时候,入度加1。 - 用一个
edges变量代表无向边数,只要值非-1,变数+1。 - 同时在遍历的过程中,针对值非-1的情况,我们将左右两端的节点进行合并。这一块使用并查集数据结构。最终合并完之后,根节点数应该只有一个。
那么我们先写并查集的数据结构。
1.1 并查集
class UnionFind {
private int[] parent;
private int[] rank;
private int sum;
public UnionFind(int n) {
rank = new int[n];
parent = new int[n];
// 初始化,每个节点的根节点指向其本身
for (int i = 0; i < n; i++) {
parent[i] = i;
}
// 这里指的是根节点数量
sum = n;
}
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
sum--;
}
}
1.2 入度以及边数检查
public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
int[] inDegree = new int[n];
UnionFind unionFind = new UnionFind(n);
// 边数
int edges = 0;
for (int i = 0; i < n; i++) {
int left = leftChild[i];
int right = rightChild[i];
if (left != -1) {
// 入度数+1,并且合并左右两端。同时边数+1
inDegree[left]++;
unionFind.union(i, left);
edges++;
}
if (right != -1) {
inDegree[right]++;
unionFind.union(i, right);
edges++;
}
}
// 判断边数是否等于 n -1
if (edges != n - 1) {
return false;
}
// 判断入度数是否都是 <=1,这里统计入度数 > 1的节点个数
int count = 0;
for (int i = 0; i < n; i++) {
if (inDegree[i] > 1) {
count++;
}
}
// 不该存在入度数 >1 的节点,如果存在,返回false
if (count > 0) {
return false;
}
// 判断是否存在环,此时根节点只能存在一个
return unionFind.sum == 1;
}
最终代码如下:
public class Test1361 {
public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
int[] inDegree = new int[n];
UnionFind unionFind = new UnionFind(n);
int edges = 0;
for (int i = 0; i < n; i++) {
int left = leftChild[i];
int right = rightChild[i];
if (left != -1) {
inDegree[left]++;
unionFind.union(i, left);
edges++;
}
if (right != -1) {
inDegree[right]++;
unionFind.union(i, right);
edges++;
}
}
// 判断边数是否相等
if (edges != n - 1) {
return false;
}
// 判断入度数是否都是 <=1
int count = 0;
for (int i = 0; i < n; i++) {
if (inDegree[i] > 1) {
count++;
}
}
if (count > 0) {
return false;
}
// 判断是否存在环
return unionFind.sum == 1;
}
class UnionFind {
private int[] parent;
private int[] rank;
private int sum;
public UnionFind(int n) {
rank = new int[n];
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
sum = n;
}
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
sum--;
}
}
}