文章目录
- 1. 并查集概念
- 2. 并查集原理
- 2.1 合并
- 2.1 找根
- 3. 并查集实现
- 3.1 结构定义
- 3.2 FindRoot(找根)
- 3.3 Union(合并)
- 3.4 IsInSet(判断两个值是否在一个集合里)
- 3.5 SetCount(并查集中集合个数)
- 3.6 测试
- 4. 并查集可以解决的问题
- 5. 并查集应用
- 5.1 省份数量
- 思路1
- AC代码
- 思路2
- AC代码
- 5.2 等式方程的可满足性
- 思路分析
- AC代码
- 6. 路径压缩
- 7. 源码
- 7.1 UnionFindSet.h
- 7.2 test.cpp
这篇文章我们来学习一个数据结构叫做并查集!

1. 并查集概念
首先我们来了解一下并查集的概念:
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。
适合于描述这类问题的抽象数据结构称为并查集(union-find set)。
2. 并查集原理
那下面我们通过一个小故事给大家讲解一下并查集的原理
假设某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。
这里呢它们就按照编号分成了三个集体。
那我们如何表示不同的集合呢?
那上面我们了解过了概念,并查集呢通常用森林来表示,一棵树就是一个集合。
上面是按编号分的,那如果我们拿到的是同学的名字,我如何知道它对应的编号是几呢?
那我就可以把名字和编号建立一个映射关系。
那我们来写写代码:
假设我们拿到的是一个名字的数组,个数为n
那我们如何存储这些数据并跟编号建立映射呢?
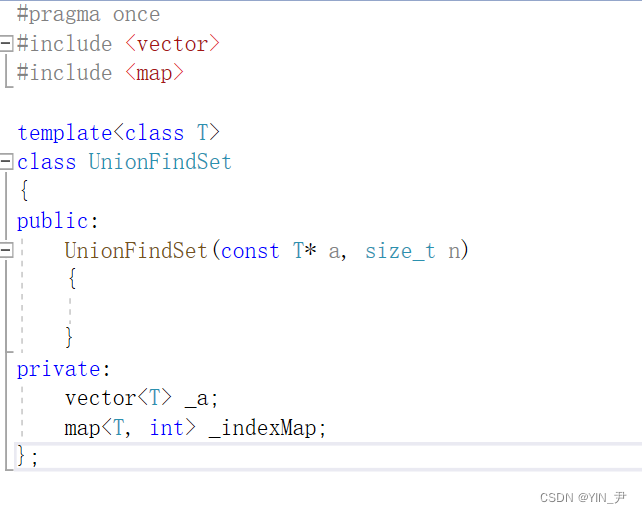
🆗,那其实我们用两个结构就可以搞定这个问题(后面我们图里面有些地方也会用到这种写法)
我们借助vector和map就可以搞定
我们可以用vector存名字数组里面的数据,那下标就可以做它们的编号,那这样用编号找名字是很方便的,编号是几,就找下标为几的元素就行了。
但是名字找编号就有点麻烦,所以我们可以借助map给名字和编号建立一个映射关系。
那我们来完善一下构造函数:
也很简单
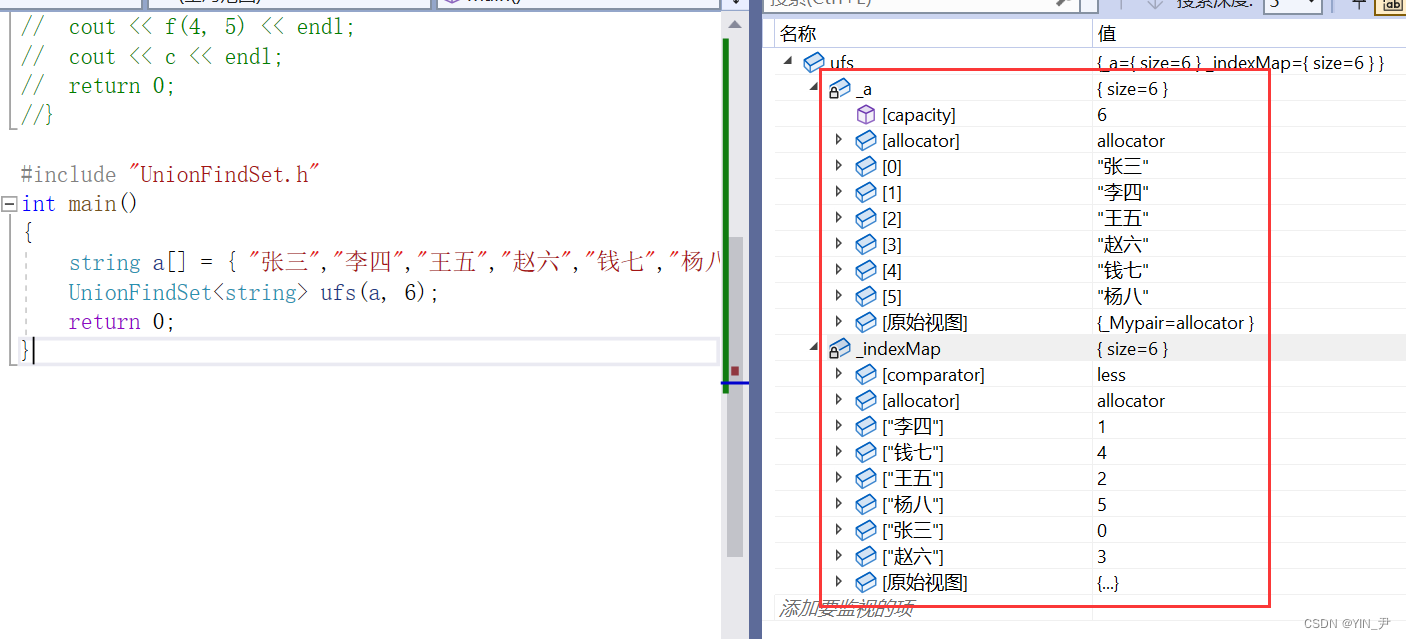
搞一组数据数据试一下:
可以
🆗,这里只是讲这样一个方法,就是不管它给我们编号还是名字我们都可以搞。
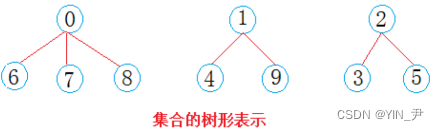
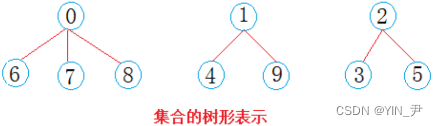
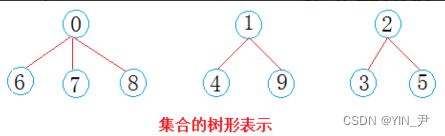
那我们再回到上面的问题:它们分成了三个集合,那我们就可以一棵树表示一个集合,3棵树的话就构成了一个森林
那我们如何用一棵树表示一个集合呢?
西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。
很简单,选一个做根,其它的做它的孩子就可以了。
假设选最小的做根(组长),负责大家的出行
那我们这里需要真的创建树吗?
🆗,其实不需要。
他这里用的是双亲表示法,用一个数组就可以搞定。
就跟我们之前学的堆有点类似,堆的逻辑结构是一棵完全二叉树,但底层的物理结构是一个数组。
那这里10个人,所以起始状态就可以这样表示
每个位置存一个-1(当然不一定非得是-1,但存-1比较好,后面会解释),现在就表示有10棵树,10个集合(还没有合并嘛)。
2.1 合并
那如何进行合并呢?
一趟火车之旅后,每个小分队成员就互相熟悉,称为了一个朋友圈,现在它们10个人分成了这样三个集体:
西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}
那我们如何在数组里把10个独立的个体合并成这样3棵树呢?
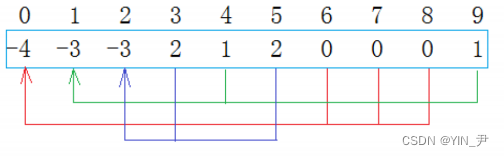
双亲表示法呢是这样搞的
解释一下
以第一棵树(0为根,6,7,8为孩子)为例,怎么做呢?
6,7,8是0的三个孩子,依次把6,7,8位置的值加到0位置上,所以0位置的值就变成了-4(起初都是-1嘛),然后6,7,8位置的值都变成0,即存它们双亲结点(或者说父结点)的下标。
另外两棵树也是同样的道理。
那这样表示呢有这样3个特点:
1. 数组的下标对应集合中元素的编号
2. 对于每个位置来说,如果它存的值是负数,那它就是根,如果不是负数,那它存的就是它的父/双亲结点的下标。
3. 根结点的位置(即值为负数的位置),该位置存的值得绝对值就是对应这棵树上结点的个数(当然前提是起始时每个位置存的都是-1,所以为什么我们上面选择了-1作为初始值)。
大家可以对照着看一下
故事继续:
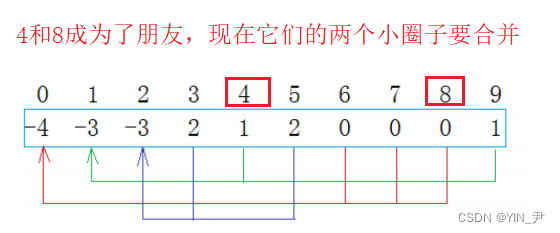
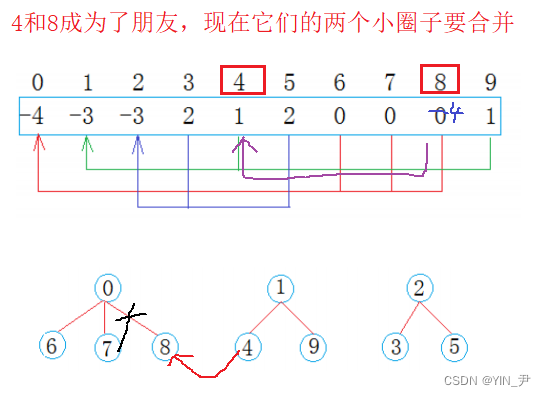
在公司工作一段时间后,西安小分队中8号同学与成都小分队4号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后融合成了一个朋友圈
那上面这种情况对应到数组中我们该怎么做呢?
可以直接像上面那样搞嘛
比如把8位置的值加到4位置上,然后8位置存4
我们一看这样肯定是不行的!
这样等于把8从原先的圈子脱离,然后加到4这棵树里面。
但是我们是要把这两个小集合合并啊,而且这样这两棵树根结点记录的个数也不对了
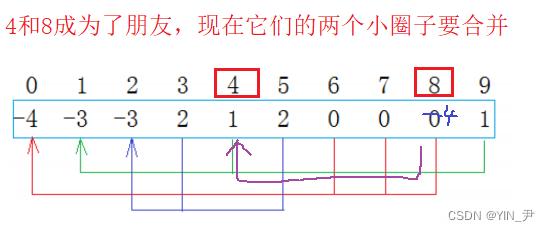
那正确的我们应该这样搞:
要找着两棵树的根,把它们的两个根合并了,这两棵树不就合并了嘛!
当然你也可以把0这棵树合并到1上边,让1做根
2.1 找根
那我们怎么找根呢?
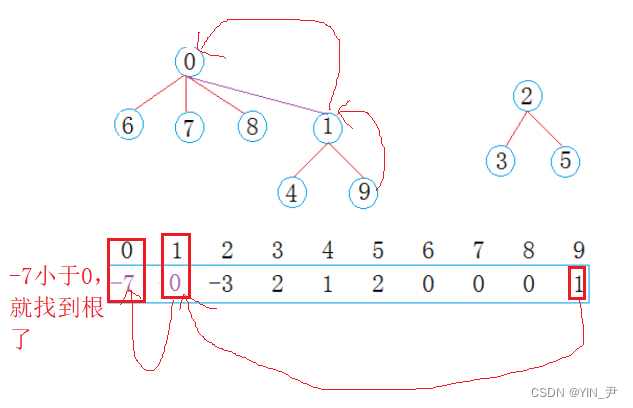
那很简单,看这个位置存的值是不是负数,是负数的话就是根了;不是负数的话,存的就是根的下标,那就顺着父结点往上找,直到值为负数就是最上面的根了
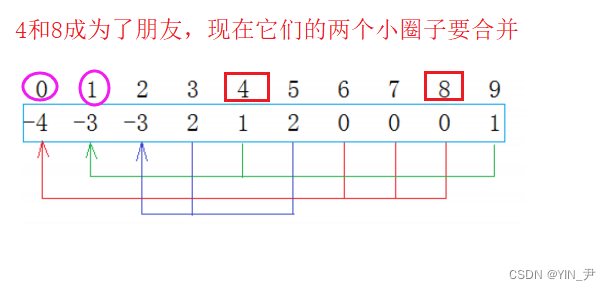
那这里:
4找到根是1,8找到根是0
然后让这两个根合并就行了,两个根你合并到我,我合并到你都可以
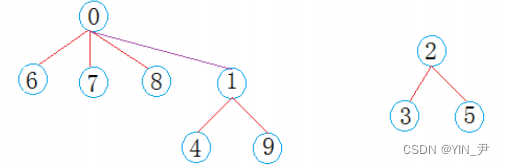
那比如我们这里让1合并到0(保持根上面一样小的做根),怎么做呢?
那就还是一样的逻辑:
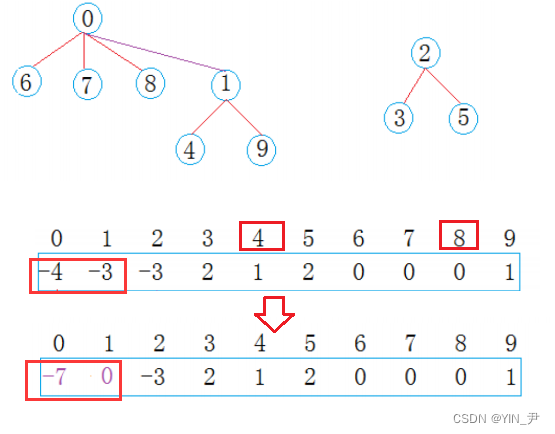
把1位置的值加到0位置上,然后1位置存0(即它的父亲的下标)
那此时0位置的值为-7,也表示0这棵树一共7个结点
现在0集合有7个人,2集合有3个人,总共两个朋友圈。
3. 并查集实现
那上面我们讲了一下并查集的原理,下面我们就来实现一个并查集,实现完再给大家做总结。
3.1 结构定义
那我们这里就不搞的像上面那样复杂了,因为我们上面的例子直接按编号去搞就行了。
那我们底层用一个vector就行了
起始全部初始化为-1
然后呢并查集主要提供以下几个接口
3.2 FindRoot(找根)
首先先来实现找根的接口,因为后面合并要用到这个接口。
怎么找呢?上面已经分析过了
如果当前位置的值是负数,那就是根了;如果不是负数,顺着父结点往上找就可以了(不是负数的话存的就是父结点的下标),遇到负数就是根了
比如:
找9的根,9位置的值不是负数,找它父亲下标为1的位置,该位置也不是负数,再找它的父亲是0,0位置是负数,所以0就是根
那我们写一下代码:
很简单
3.3 Union(合并)
那这里的合并呢就是给两棵树(集合)的根,把这两个集合合并为一个集合:
那这个接口怎么实现呢?
那我们上面其实已经分析过了:
不能直接合并,要找根。
如果是两个单个元素的集合合并可以直接合(因为可以认为它们自己就是根),但是如果是两个多个元素的集合就不能直接合并,而是要找到两个根,把两个根进行合并
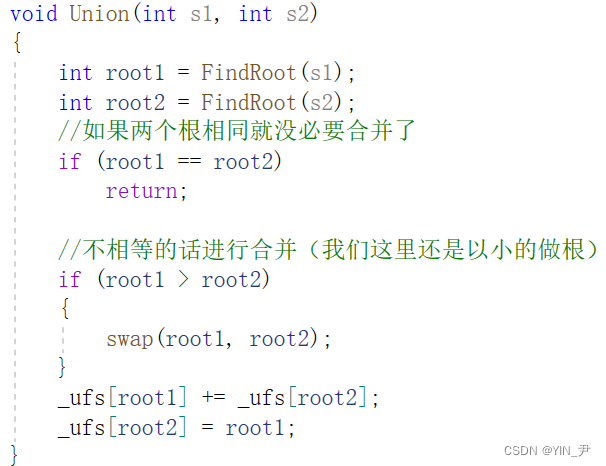
但是找到根之后我们要判断一下这两个根一样不一样,一样的话就没必要合并了(证明它们俩本来就在一个集合里或者是同一个值)
然后不同的话就进行合并(如何合并我们前面讲过了)
写一下代码:
3.4 IsInSet(判断两个值是否在一个集合里)
那这个很简单,判断这两个值所在集合的根一不一样就行了,一样就在一个集合,不一样就不在:
3.5 SetCount(并查集中集合个数)
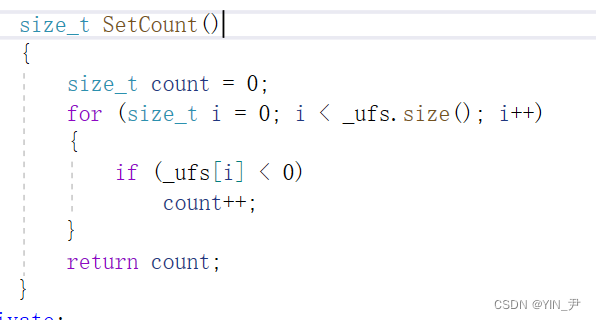
还有一个接口就是计算并查集中集合的个数:
非常简单,统计一下vector里面一共有多少个负数就有几个集合,因为一个负数对应的下标就是一棵树的根
写一下:
3.6 测试
简单测试一下:
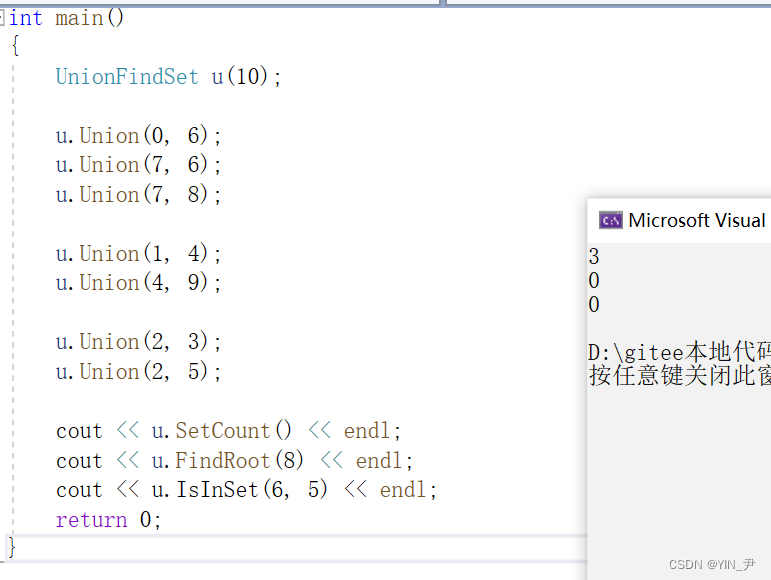
没问题。
4. 并查集可以解决的问题
通过以上学习可知,并查集一般可以解决一下问题:
1. 查找元素属于哪个集合(找根)
沿着数组表示的树形关系往上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合
4. 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数
5. 并查集应用
那下面我们来做两个题
5.1 省份数量
题目链接: link
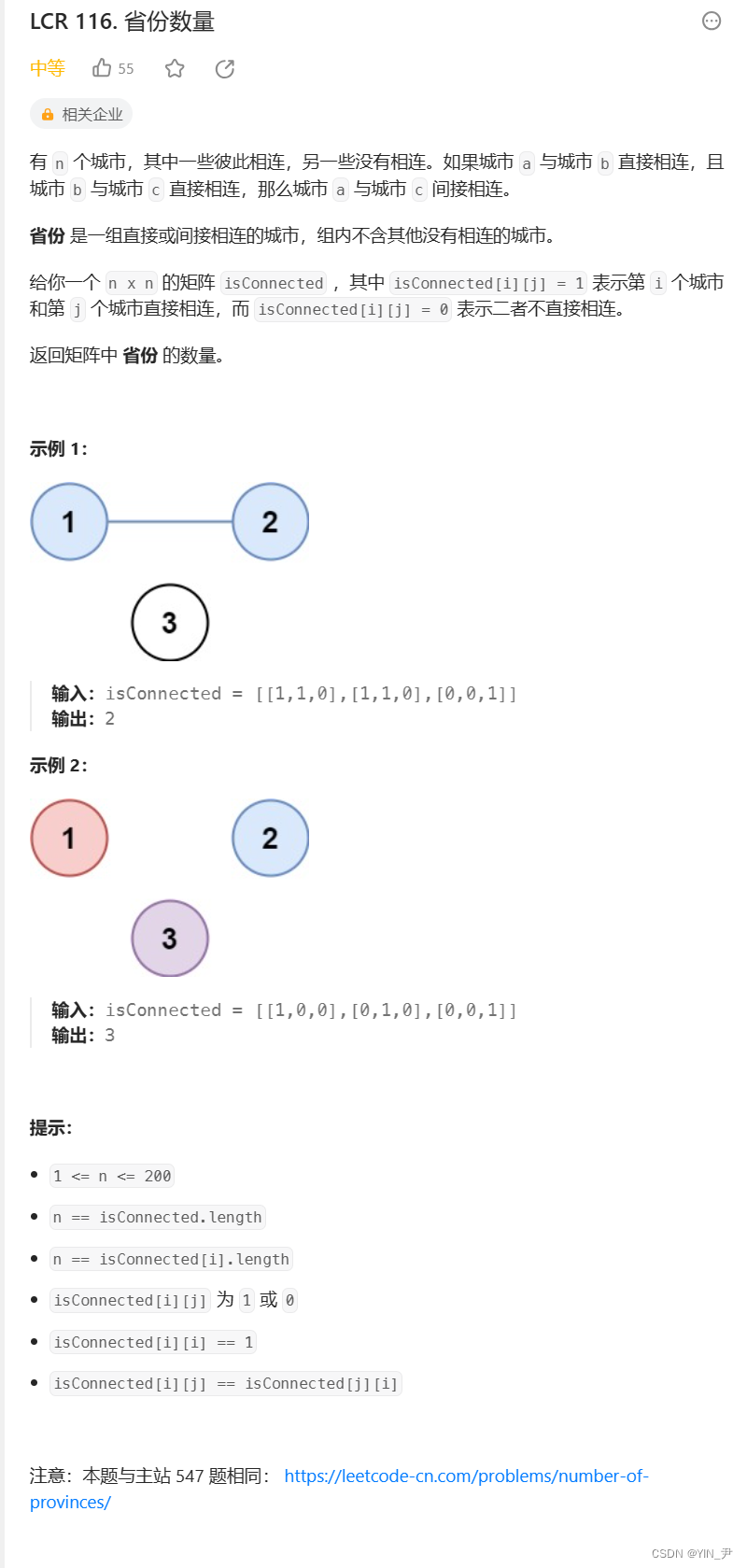
大家自己先看一下题
思路1
我们来分析一下题目:
题目给我们一共N*N的二维数组isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连
另外如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
让我们返回矩阵中 省份 的数量
这里对于省份的定义是:省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市
那这道题其实用并查集来解决就很简单:
其实就是找集合的个数嘛。
把我们实现的并查集拷过来,定义一个并查集,然后把相连的城市合并到一个集合里面,最终统计集合的个数就行了。
很简单!
AC代码
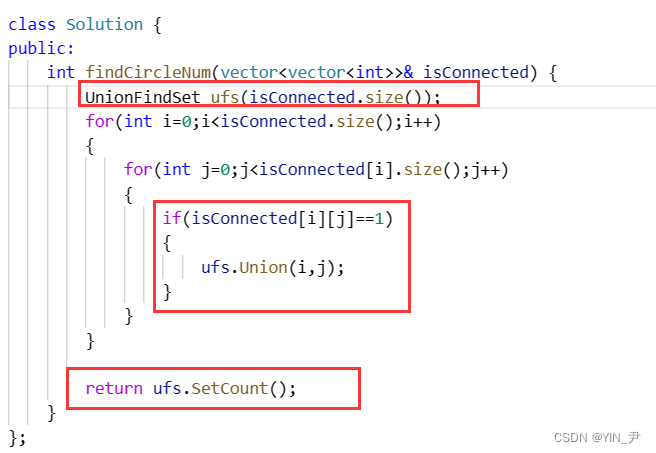
class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
int FindRoot(int x)
{
int root = x;
while (_ufs[root] >= 0)
{
root = _ufs[root];
}
return root;
}
void Union(int s1, int s2)
{
int root1 = FindRoot(s1);
int root2 = FindRoot(s2);
//如果两个根相同就没必要合并了
if (root1 == root2)
return;
//不相等的话进行合并(我们这里还是以小的做根)
if (root1 > root2)
{
swap(root1, root2);
}
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
bool IsInSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetCount()
{
size_t count = 0;
for (size_t i = 0; i < _ufs.size(); i++)
{
if (_ufs[i] < 0)
count++;
}
return count;
}
private:
vector<int> _ufs;
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet ufs(isConnected.size());
for(int i=0;i<isConnected.size();i++)
{
for(int j=0;j<isConnected[i].size();j++)
{
if(isConnected[i][j]==1)
{
ufs.Union(i,j);
}
}
}
return ufs.SetCount();
}
};
思路2
然后呢想说的是:
我们上面的方法呢,很简单,但是前提是我们已经写好了一个并查集。
那以后遇到这种题都需要我们手撕一个并查集吗?
其实不需要完整的手撕一个,直接用并查集的思想解题就行了。
AC代码
我们来写一下:
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int> ufs(isConnected.size(),-1);
auto FindRoot=[&ufs](int x)
{
while(ufs[x]>=0)
{
x=ufs[x];
}
return x;
};
for(int i=0;i<isConnected.size();i++)
{
for(int j=0;j<isConnected[i].size();j++)
{
if(isConnected[i][j]==1)
{
int root1=FindRoot(i);
int root2=FindRoot(j);
if(root1!=root2)
{
ufs[root1]+=ufs[root2];
ufs[root2]=root1;
}
}
}
}
int count=0;
for(auto e:ufs)
{
if(e<0)
count++;
}
return count;
}
};
5.2 等式方程的可满足性
题目链接: link

大家看一下题目
思路分析
这道题分析一下其实就是看他给我们的所有条件能不能全部同时成立。
用并查集去搞其实就很简单,我们来分析一下:
那这里呢我们还是用一个并查集,当然不一定非得写一个完整的并查集,就可以像上一题第二种方法那样,用到什么接口自己简单实现一下就行了。
然后呢我们可以这样搞:
因为题目给的变量之间的关系只有==和!=嘛。
首先,遍历一遍字符串方程的数组,把相等关系的变量放到一个集合里面;
然后第二遍遍历,判断不相等关系的变量是否在一个集合中,如果有在的,那他们就不能同时成立(返回false),如果没有就可以(返回true)
判断相不相等只需要看equations[i][1]就可以了
AC代码
我们来写一下代码:
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
vector<int> ufs(26,-1);
auto FindRoot=[&ufs](int x)
{
while(ufs[x]>=0)
{
x=ufs[x];
}
return x;
};
//第一次遍历把相等关系的变量放到一个集合里面
for(auto str:equations)
{
if(str[1]=='=')
{
int root1=FindRoot(str[0]-'a');
int root2=FindRoot(str[3]-'a');
if(root1!=root2)
{
ufs[root1]+=ufs[root2];
ufs[root2]=root1;
}
}
}
//第二次遍历判断不相等关系的变量是否在一个集合中,
//如果有在的,那他们就不能同时成立
for(auto str:equations)
{
if(str[1]=='!')
{
int root1=FindRoot(str[0]-'a');
int root2=FindRoot(str[3]-'a');
if(root1==root2)
{
return false;
}
}
}
return true;
}
};
6. 路径压缩
然后呢关于压缩路径的问题这里也简单提一下:
这个东西呢其实就是对并查集的一个优化。
其实我们平时写都不太需要考虑这个东西,除非数据量特别大的时候,可能有些路径会比较长,导致效率变慢,这时候可以考虑进行一下压缩。
那压缩呢其实就是在FindRoot这里面进行一些操作,举个例子简单给大家说一说:
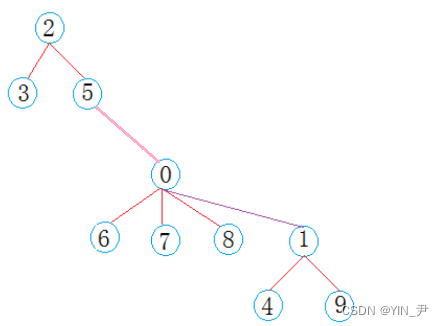
比如现在是这样一个情况
那压缩的话就是查找谁就去压谁,当然不是所有的路径都需要压缩。
比如Find3的话,那里面判断一下,就一层,不需要压缩。
再比如,查找6
那最后发现它返回的root是2,但是6直接的上一层的父亲并不是2,
那说明它们之间有间隔层,那就可以对这条路径压缩一下。
可以直接把6变成2的孩子,那后续再查找6的话就快了。
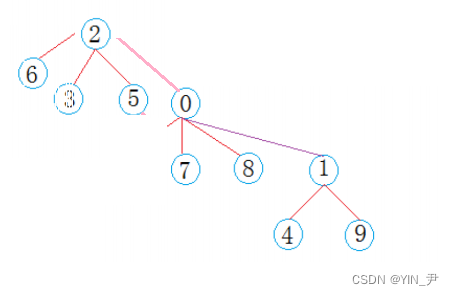
然后也可以直接把6的上一层父亲,0直接变成2的孩子
所以我们这样是边找边压缩,比如后面再找9的话,就可以再把9变成2的孩子,然后顺着这条路径再把1变成2的孩子(如果更长的情况就一直往上就行了)
就是在FindRoot里面再加一个压缩路径的代码,其实就是先找到根结点,然后把这条查找路径上所有的结点都直接链接到根结点上。
当然数据量小的时候就完全没有必要做这个事情。
代码给大家写一下:
7. 源码
7.1 UnionFindSet.h
#pragma once
//#include <map>
//
//template<class T>
//class UnionFindSet
//{
//public:
// UnionFindSet(const T* a, size_t n)
// {
// for (size_t i = 0; i < n; i++)
// {
// _a.push_back(a[i]);
// _indexMap[a[i]] = i;
// }
// }
//private:
// vector<T> _a;
// map<T, int> _indexMap;
//};
class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
int FindRoot(int x)
{
int root = x;
while (_ufs[root] >= 0)
{
root = _ufs[root];
}
return root;
}
void Union(int s1, int s2)
{
int root1 = FindRoot(s1);
int root2 = FindRoot(s2);
//如果两个根相同就没必要合并了
if (root1 == root2)
return;
//不相等的话进行合并(我们这里还是以小的做根)
if (root1 > root2)
{
swap(root1, root2);
}
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
bool IsInSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetCount()
{
size_t count = 0;
for (size_t i = 0; i < _ufs.size(); i++)
{
if (_ufs[i] < 0)
count++;
}
return count;
}
private:
vector<int> _ufs;
};
7.2 test.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
using namespace std;
#include <vector>
//#include "UnionFindSet.h"
//int main()
//{
// string a[] = { "张三","李四","王五","赵六","钱七","杨八" };
// UnionFindSet<string> ufs(a, 6);
// return 0;
//}
#include "UnionFindSet.h"
int main()
{
UnionFindSet u(10);
u.Union(0, 6);
u.Union(7, 6);
u.Union(7, 8);
u.Union(1, 4);
u.Union(4, 9);
u.Union(2, 3);
u.Union(2, 5);
cout << u.SetCount() << endl;
cout << u.FindRoot(8) << endl;
cout << u.IsInSet(6, 5) << endl;
return 0;
}