Description

OiersOiers 国的预警系统是一棵树，树中有 �n 个结点，编号 1∼�1∼n，树中每条边的长度均为 11。预警系统中只有一个预警信号发射站，就是树的根结点 11 号结点，其它 �−1n−1 个结点是接收中转站。
每当有险情发生时，11 号结点就会向 �x 号结点发送预警信号，然后由 �x 号结点将预警信号传送到离 11 号结点距离为 �y 的所有结点，注意：所有传送是单向的，都是由根结点向叶子结点方向传送，请参考样例。
你的任务是计算每次发送预警时，�x 号结点需要将预警信号传送到离 11 号结点距离为 �y 的结点个数。

Input

第一行一个整数 �n。
第二行 �−1n−1 个整数 ��2,��3,⋯,���fa2​,fa3​,⋯,fan​ 描述树，整数 ���fai​ 表示结点 �i 的父亲结点为 ���(2≤�≤�)fai​(2≤i≤n)。
第三行一个整数 �m，表示有 �m 次险情发生，需要发送 �m 次预警信号，即有 �m 次询问。
接下来 �m 行，每行两个整数 �,�x,y。

Output

输出 m 行，每行一个整数，表示�x 号结点需要将预警信号传送到离 11 号结点距离为 �y 的结点个数。

Sample Input

7
1 2 2 2 1 3
4
1 2
5 2
4 1
3 5

Sample Output

3
1
0
0

Sample Explanation

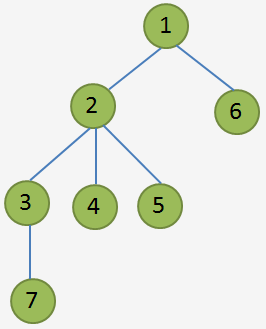
在第一个询问中，由 11 号结点传送到距 11 号结点距离为 22 的结点有 3,4,53,4,5 三个结点。
在第二个询问中，由 55 号结点传送到距 11 号结点距离为 22 的结点只有 55 号自身一个结点。
在第三个询问中，由 44 号结点传送到距 11 号结点距离为 11 的结点不存在，因为传送只能往下进行。
在第四个询问中，由 33 号结点传送到距 11 号结点距离为 55 的结点不存在。

Hint

本题共 2525 个测试点，其中：
20%20% 的数据：1≤�≤1001≤n≤100，1≤�≤101≤m≤10；
另有 12%12% 的数据：1≤�≤1001≤n≤100，1≤�≤101≤m≤10，树为一条链；
100%100% 的数据：2≤�≤2×1052≤n≤2×105，1≤���<�1≤fai​<i，1≤�≤2×1051≤m≤2×105，1≤�≤�1≤x≤n，0≤�≤�−10≤y≤n−1。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,u,y,id,time_id,d[200009],tim_in[200009],tim_out[200009],head[200009];
vector<int> v[200009];
struct edge{
	int u,v,next;
}e[400009];
void add(int u,int v){
	e[++id]=edge{u,v,head[u]};
	head[u]=id;
}
void dfs(int u,int fa){
	d[u]=d[fa]+1;
	tim_in[u]=++time_id;
	v[d[u]].push_back(tim_in[u]);
	for(int i=head[u];i;i=e[i].next) dfs(e[i].v,u);
	tim_out[u]=time_id;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=2;i<=n;i++){
		cin>>u;
		add(u,i);
	}
	d[0]=-1;
	dfs(1,0);
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>y;
		cout<<upper_bound(v[y].begin(),v[y].end(),tim_out[u]) - lower_bound(v[y].begin(),v[y].end(),tim_in[u])<<'\n';
	}
	return 0;
}

总结：

这题得用一种叫DFS序的东西，二分求最值