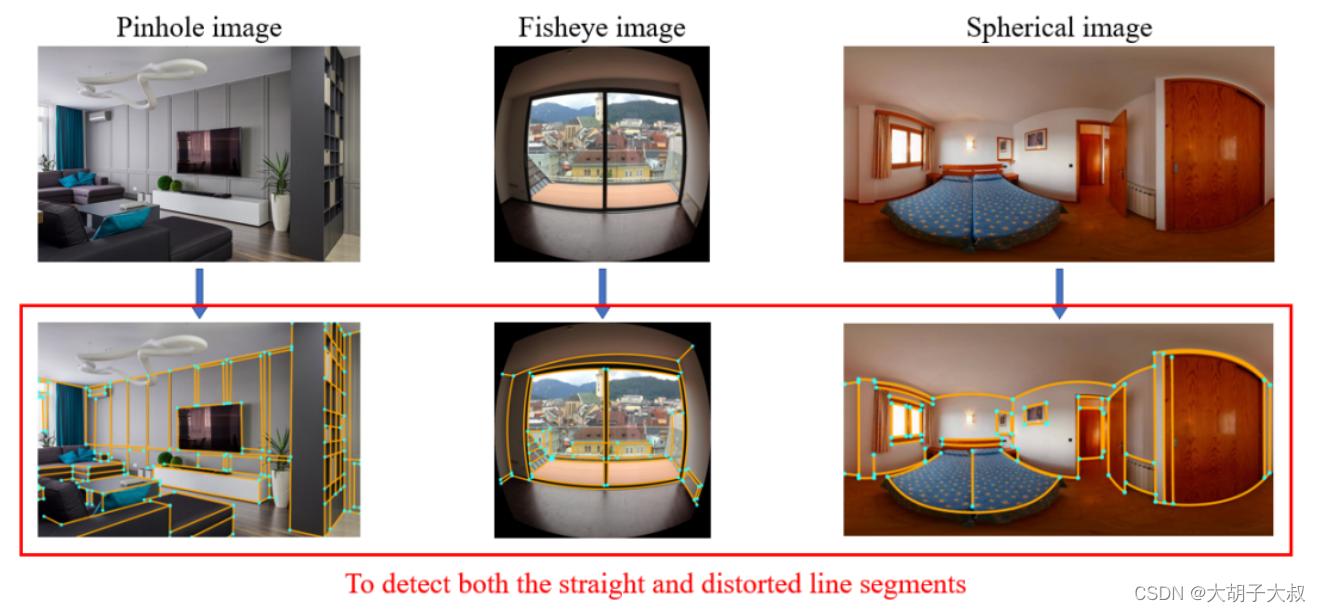
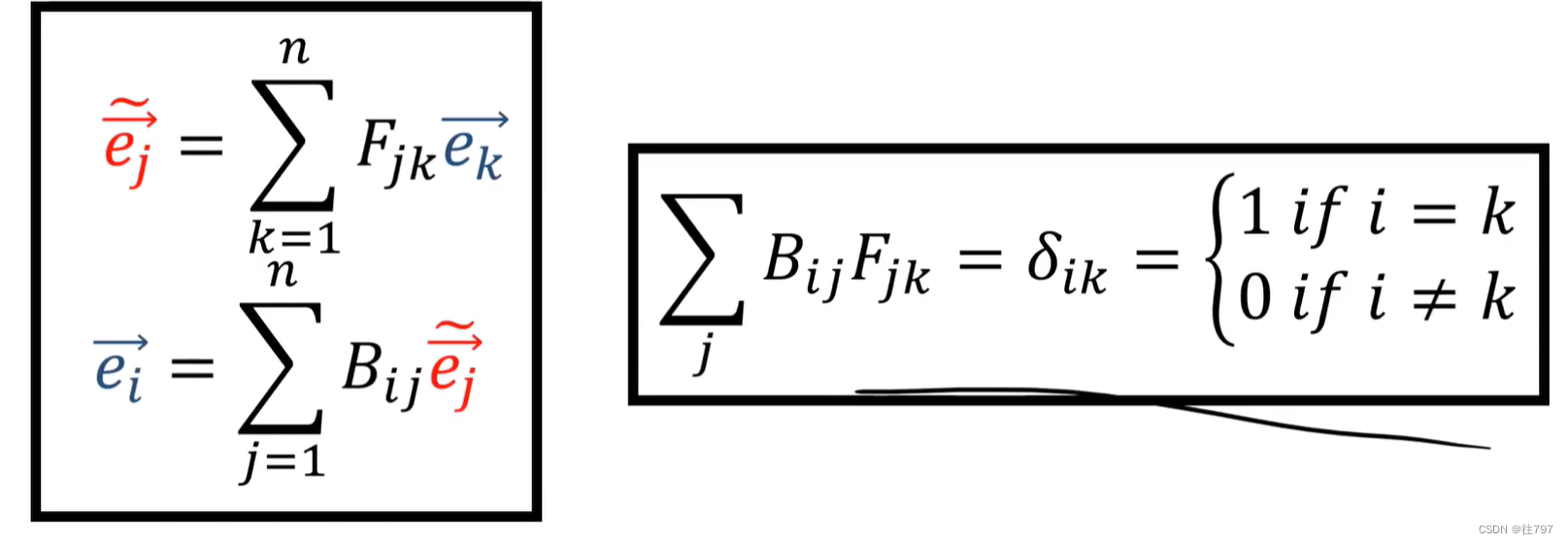张量在不同坐标系之间来回移动的规则究竟如何。
之前说过，张量在坐标系变化下是不变的，故了解如何在坐标系之间来回移动对理解张量很重要。
Forward：旧基 到 新基
old basis：旧基
这是在二维坐标系下的两组基。
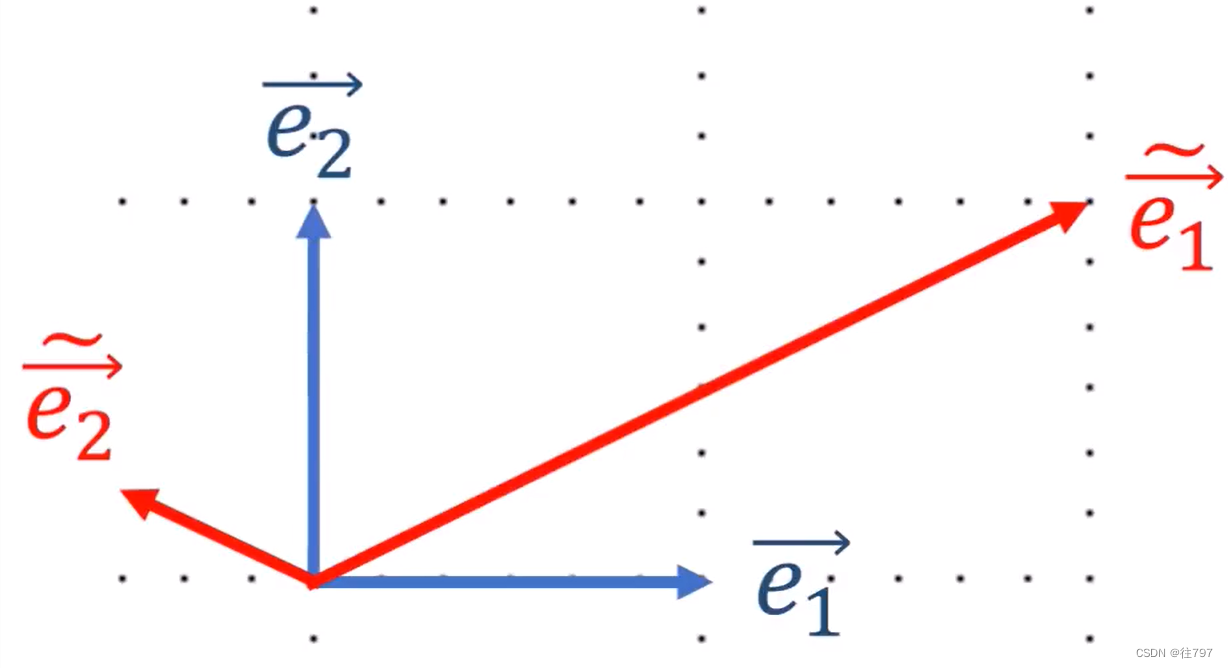
线性代数中的基： 向量空间V中的一组向量 若满足：
1）线性无光
2）向量中间V中的任何一个向量 都可由 该组向量 线性表出，
则称该组向量为 向量空间V的 一组基
前向变换（Forward）：从旧基转移到新基
如何转移？
--------------利用旧基向量 构建 新基向量
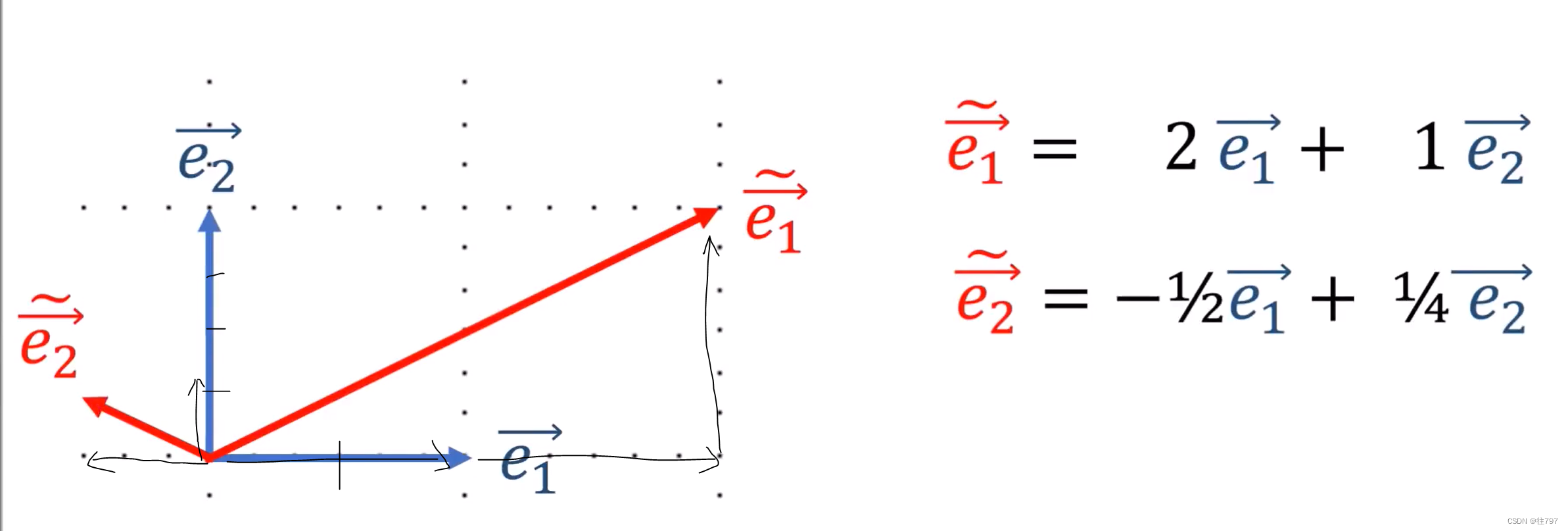
用旧基的线性组合来表示新基
可将这四个系数存储到一个2 x 2的矩阵F中，
矩阵F就是正向变换。
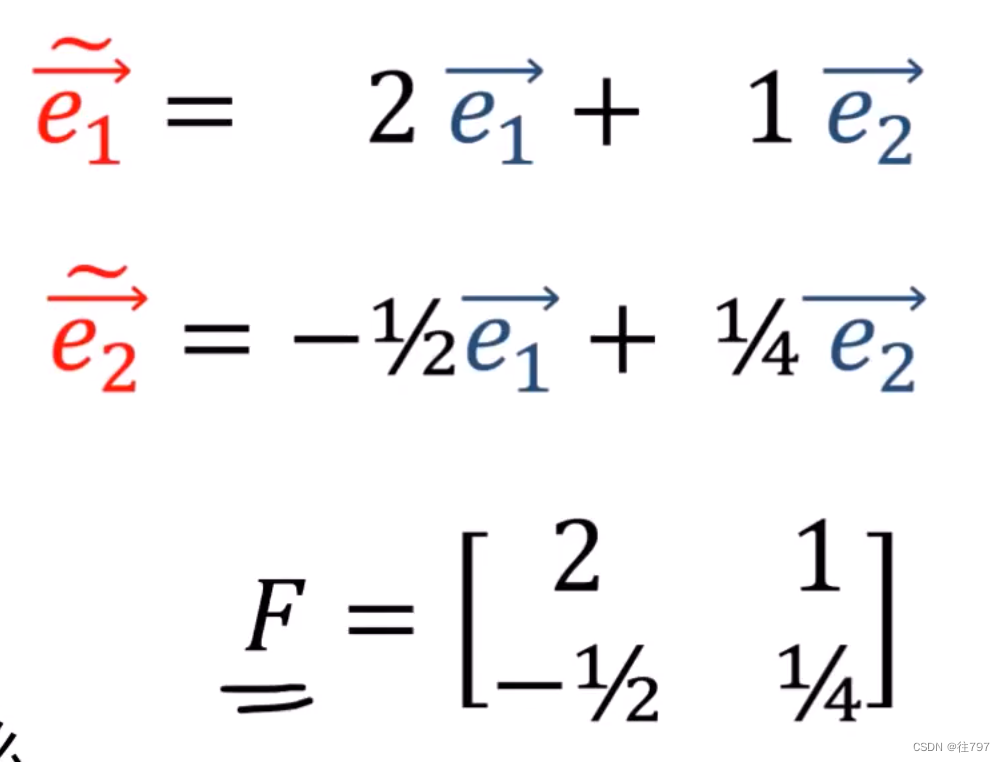
后向变换（Backward）：从新基转移到旧基
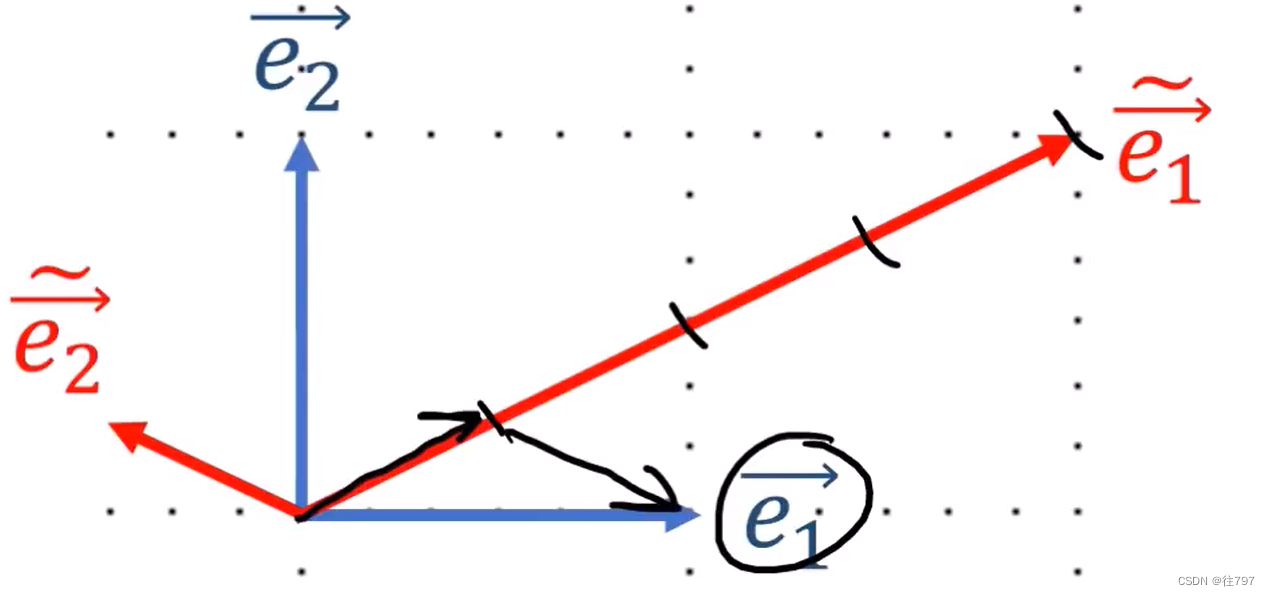
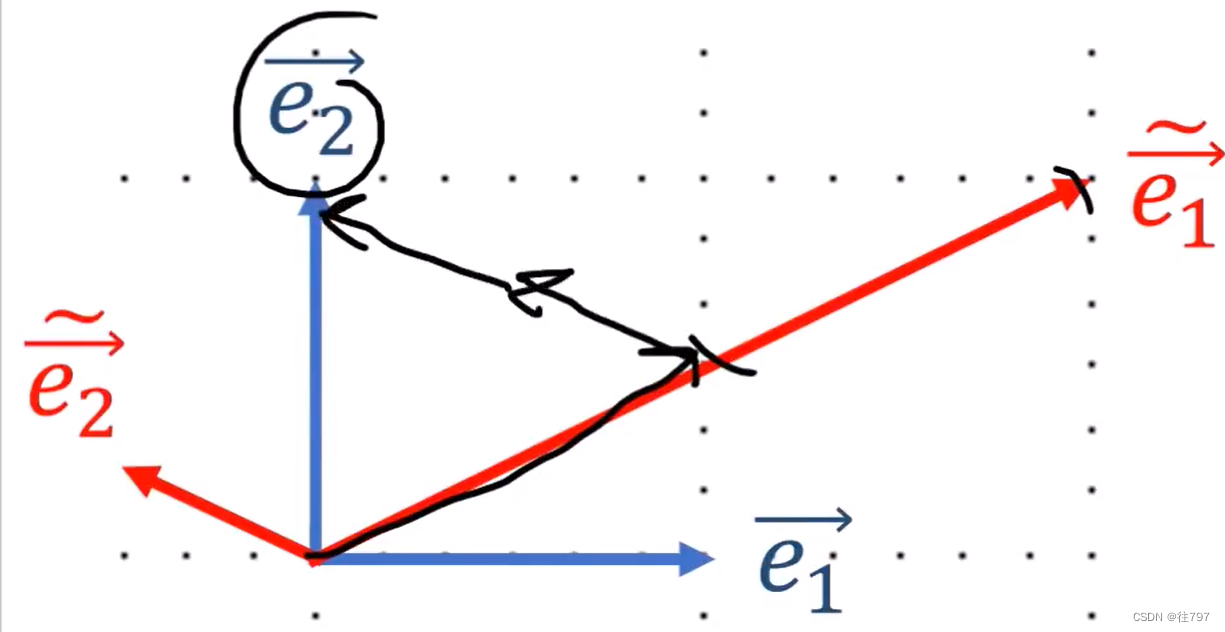
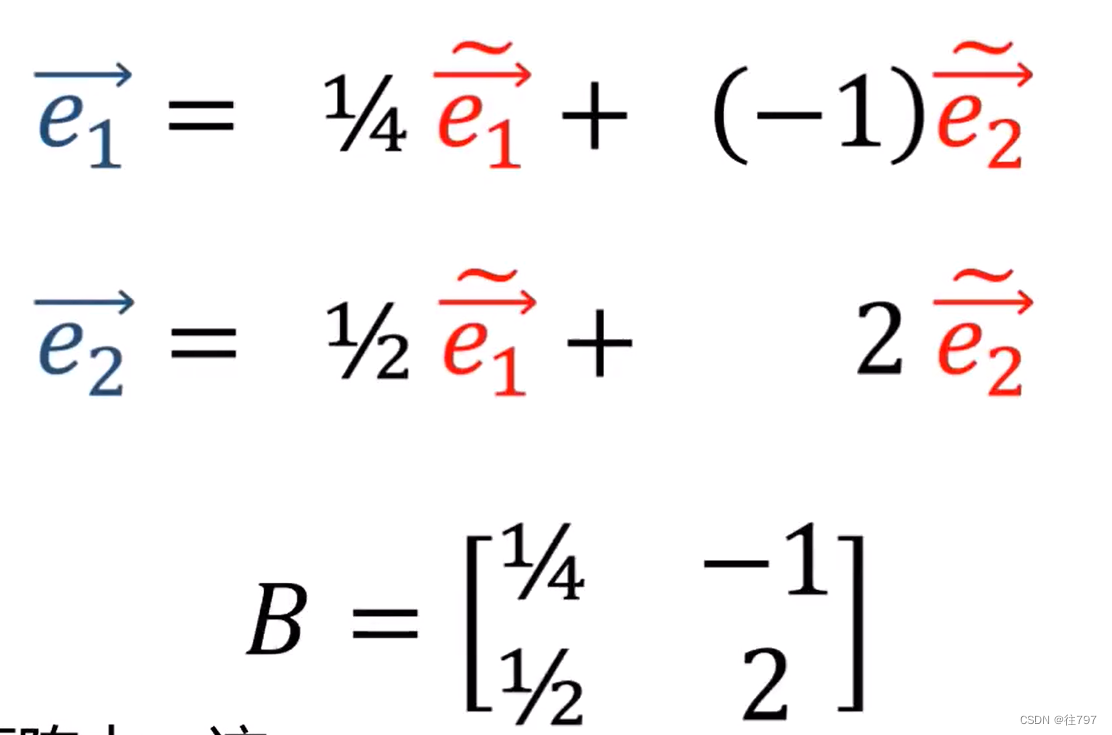
知道这个矩阵B后，就知道如何进行后向转换了，如何从新基转移到旧基
把向前转换 和 向后转换 两个矩阵进行相乘， F*B= E
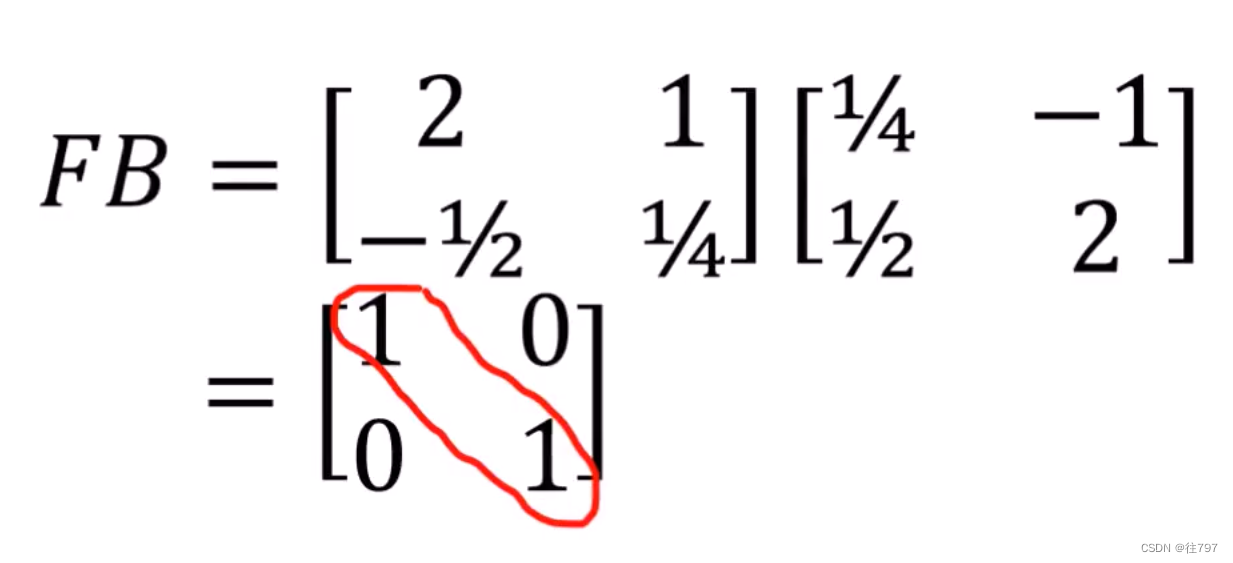
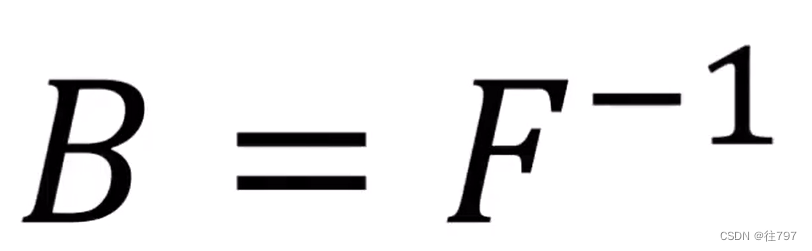
解释：
两边左乘
；
即
这是二维的例子。
现推广到n维，
也是类似的，有n个旧基：，n个新基
，
向前转换：Forward
但这么多方程看起来有点烦人，
试试用公式简化
观察一下上图，就能写出下式：
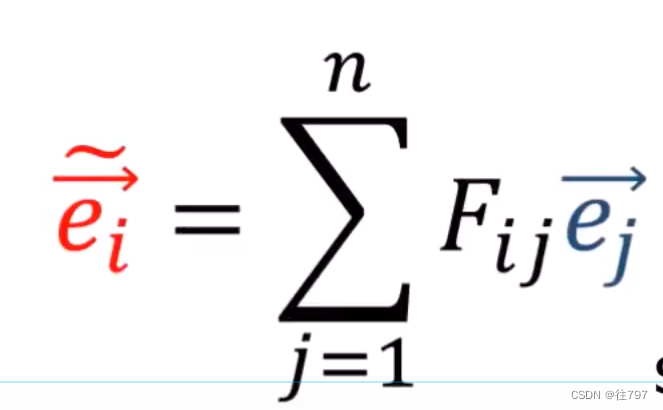
一个新基 由 旧基中的所有向量的线性组合表示
该公式总结了上述的所有方程。
后向变换：Backward
也是类似的
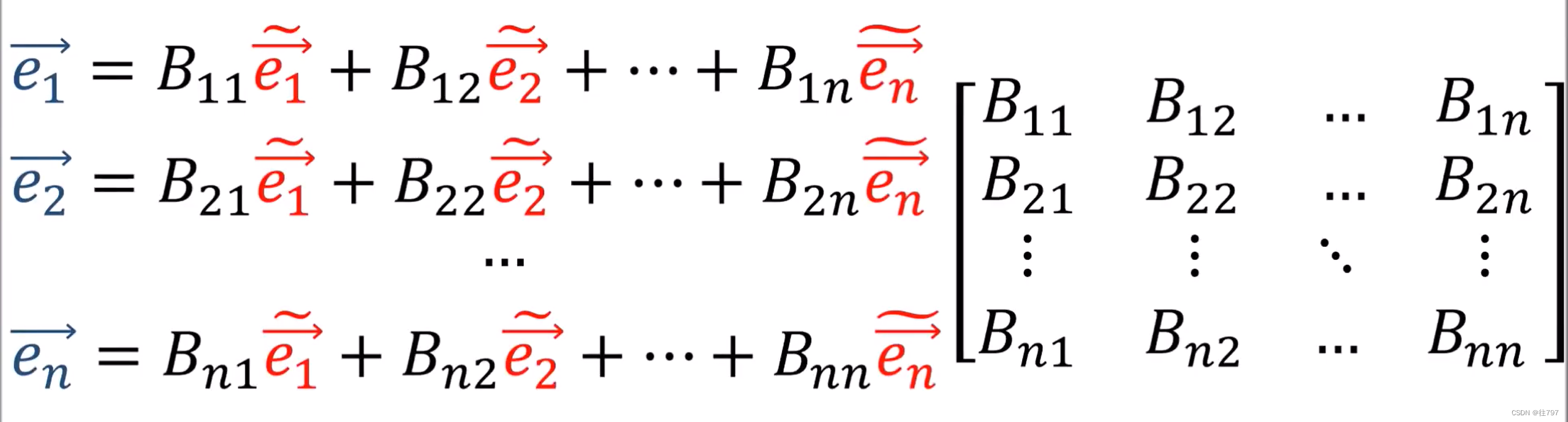
用新基的所有向量的线性组合来表示 旧基中的任一向量
并把这些系数写到一个 n x n的矩阵B中
同样的道理，可以用一个公式来总结 上述n个方程。
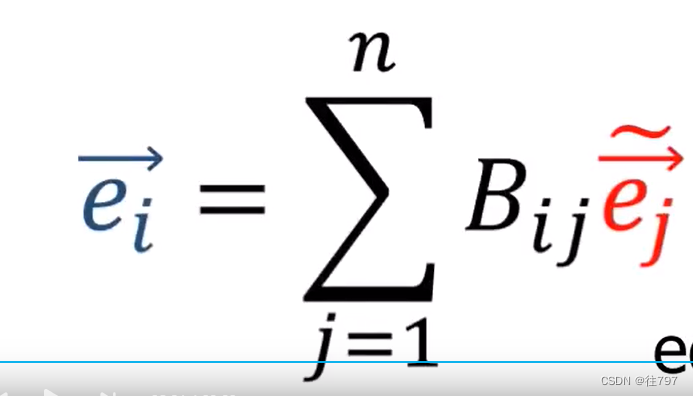
对于获得的两个矩阵，我们如何证明它们是互逆的？
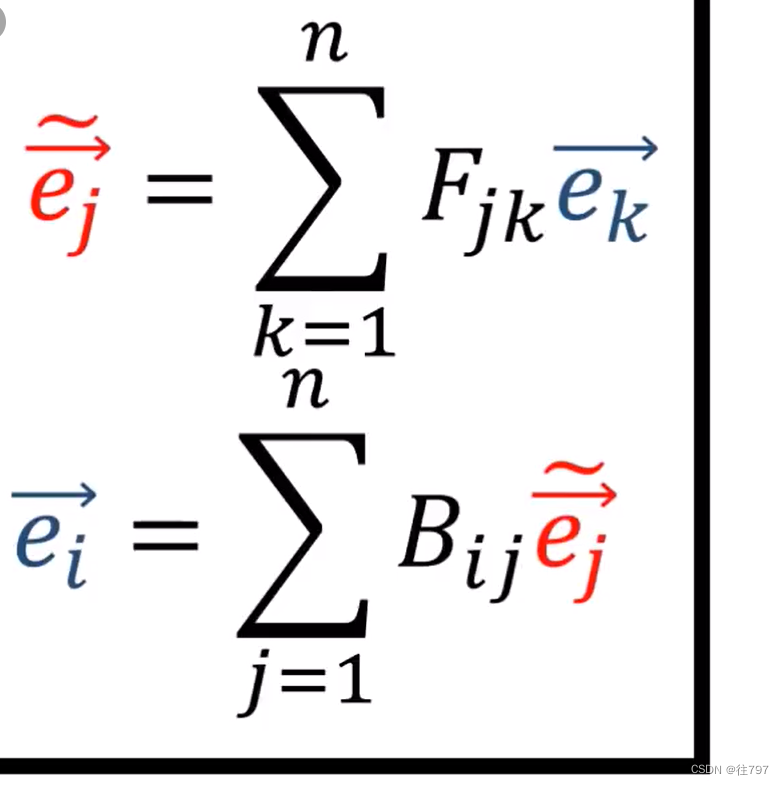
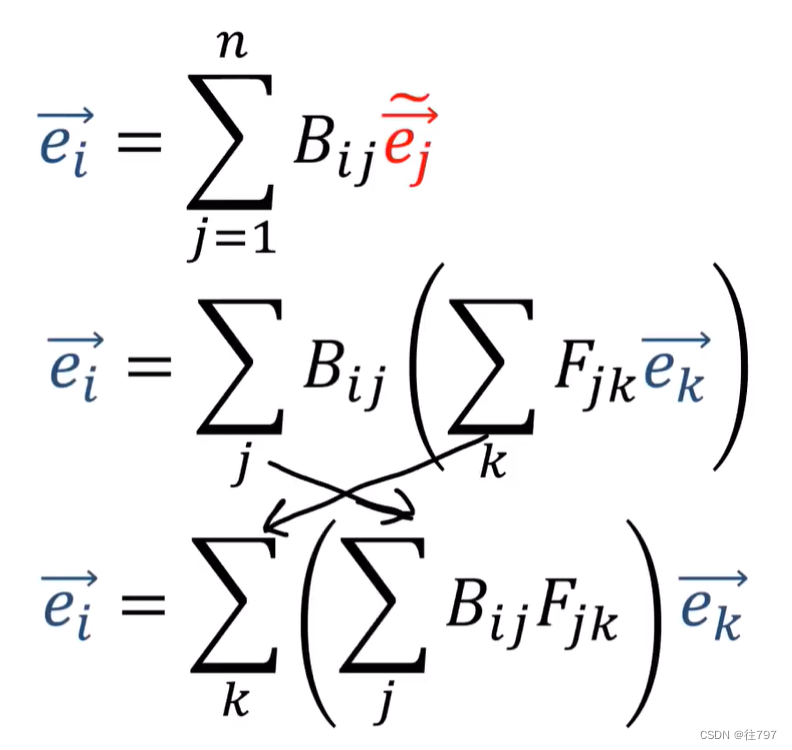
观察上面最底下的这个式子， 其不就是在用 n个旧基向量的求和 来 构建一个 旧基向量吗，
那么中间那部门应该等于多少？
当然是 k==i 时，中间那部分就为1， 当 k ≠ i 时，中间那块为0.
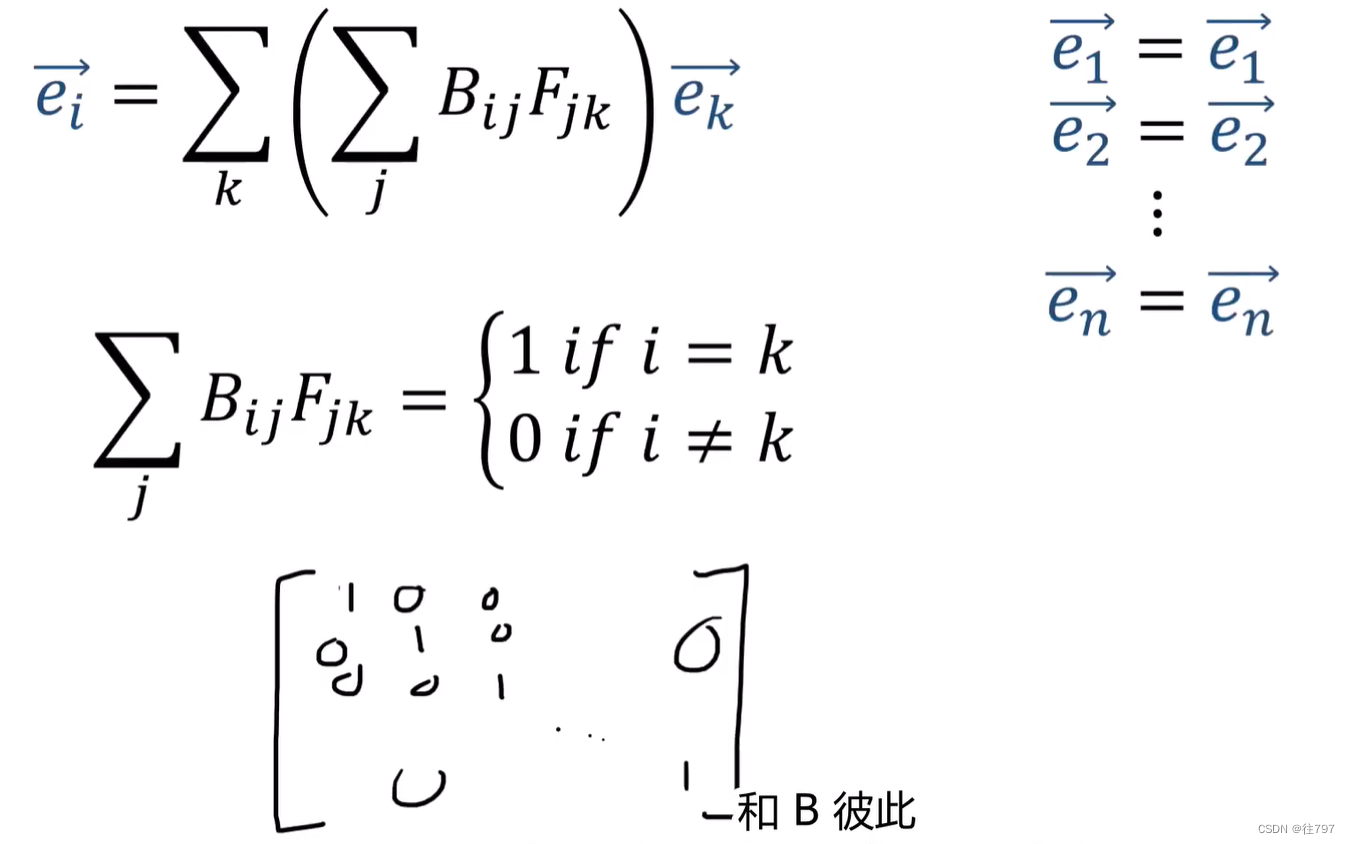
这种 if i = k，就为1； if i≠k，就为0； 是普遍现象，我们把它称为Kronecker Delta
就是表示出一个单位矩阵
解释：
两边左乘
即
