数字IC前端学习笔记：数字乘法器的优化设计（进位保留乘法器）

news2025/1/16 2:05:56

相关阅读

数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482

阵列乘法器设计中限制乘法器速度的是随着数据位宽而迅速增大的串行进位链，如果使用进位保留加法器，则可以避免在设计中引入较长时间的等待，即可以将两、三个数相加时不同比特位的加法割裂开，使进位得到保留而不是立刻将进位传递给更高位运算，进位保留加法器的结构如图1所示。

图1 进位保留乘法器

其实进位保留加法器和普通全加器的内部结构一模一样，但不同的是对于进位的处理，普通的全加器接受两位加数和一位进位，输出一位和以及一位进位。而保留进位加法器接受三位加数的输入，输出两位，具体的转换如图2所示。

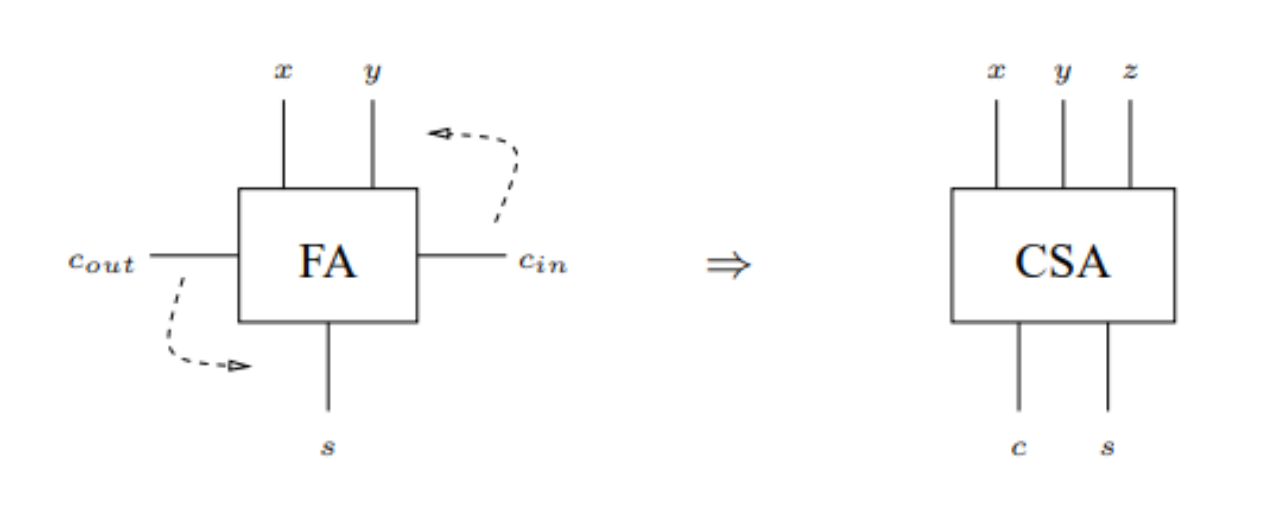图2 全加器和保留进位加法器的转换

使用保留进位加法器组成多位加法器时，本文采用了与传统串行进位加法器不同的设计方案，不是将多个全加器首尾相连方式串行传播进位信号，而是多个保留进位加法器并行输出，因为这种保留进位加法器输入三位，输出两位，所以也把它叫做3-2压缩器（3-2 compressor）。

进位保留乘法器的结构图如图3所示，可以看到，与之前的阵列乘法器相比，进位保留乘法器对于输出的进位，并不将其传递给本级的高位加法器，而是传递给下一级的高位乘法器，在最后一级使用一个被称为向量合并加法器（图中用绿色框出）的模块来处理最后的两个多位二进制数。向量合并加法器可以选择普通的串行进位加法器或者超前进位加法器，还可以是其他高效的加法器。四位进位保留加法器的资源规划如表1所示。

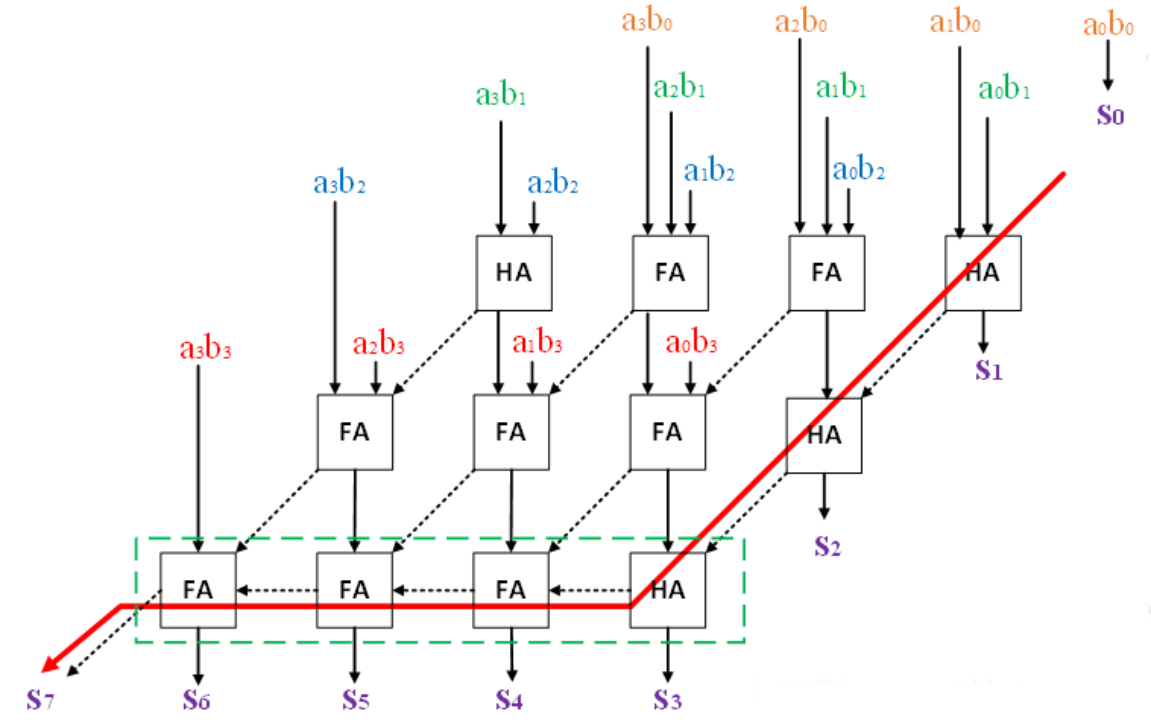图3 进位保留乘法器结构

表4-1 无符号4位二进制乘法规划

				A3 B3	A2 B2	A1 B1	A0 B0	被乘数乘数	资源配置
			A3B1	A3B0 A2B1	A2B0 A1B1	A1B0 A0B1	A0B0	部分积0 部分积1 上级进位	第1行加法器
		C13 A3B2	S13 A2B2 C12	S12 A1B2 C11	S11 A0B2 C10	S10	S00	第1行和部分积2 上级进位	第2行乘法器
	C23 A3B3	S23 A2B3 C22	S22 A1B3 C21	S21 A0B3 C20	S20			第2行和部分积3 上级进位	第3行乘法器
C33	S33	S32	S31	S30				第3行和	向量合并加法器
	C32	C31	C30					第3行和	向量合并加法器

具体的Verilog代码实现见附录，Modelsim软件仿真截图如图4所示。使用Synopsis的综合工具Design Compiler综合的结果如图5所示，综合使用了0.13μm工艺库。

图4 进位保留乘法器仿真结果

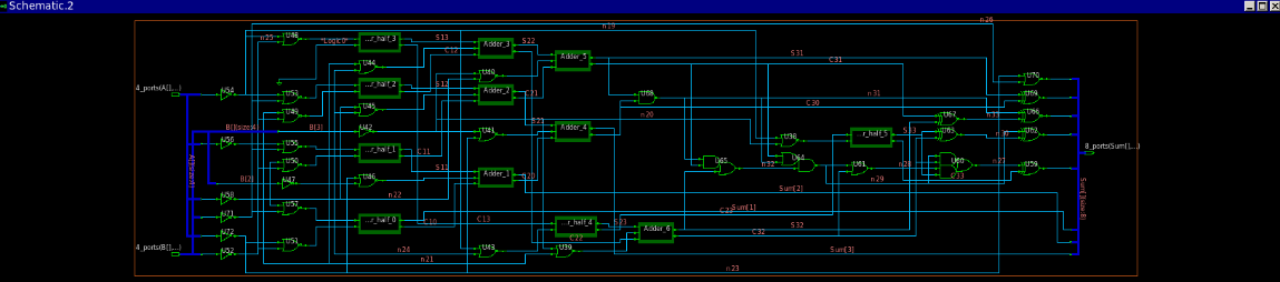图5 进位保留乘法器综合结果

在Design Compiler中使用report_timing命令，可以得到关键路径的延迟，如图6所示。使用report_area命令，报告所设计电路的面积占用情况，如图7所示。

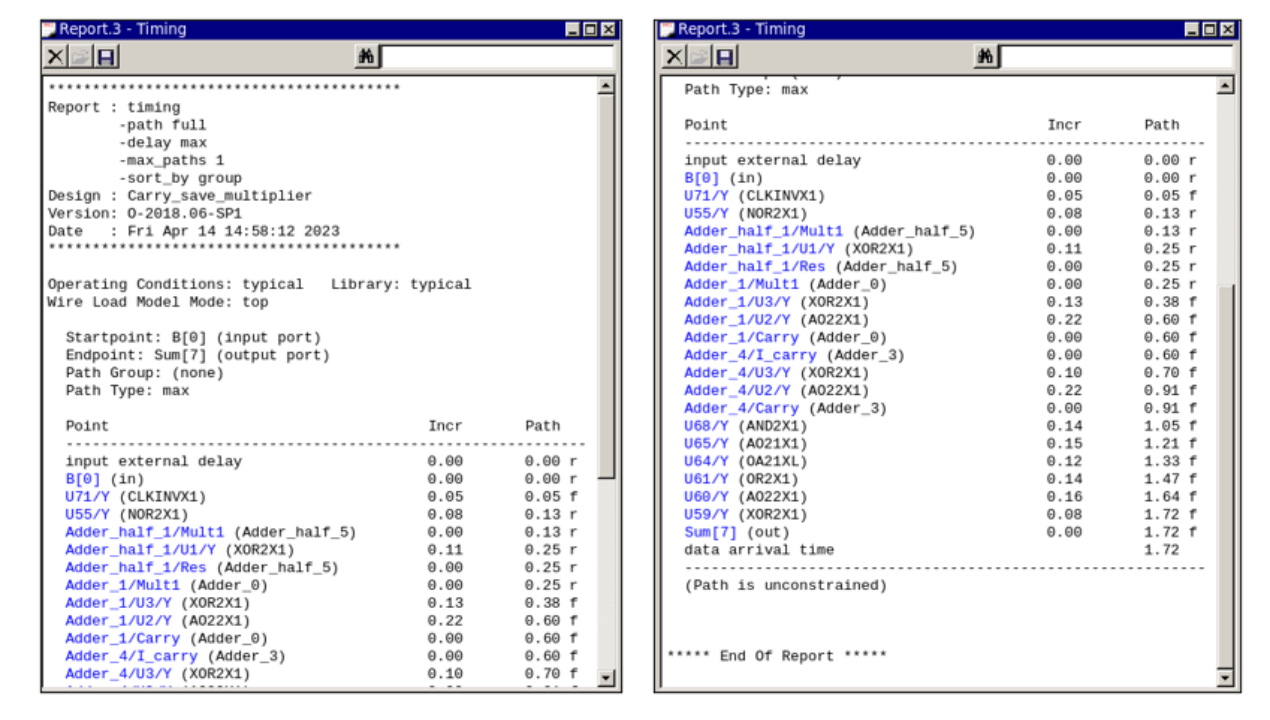图6 关键路径报告

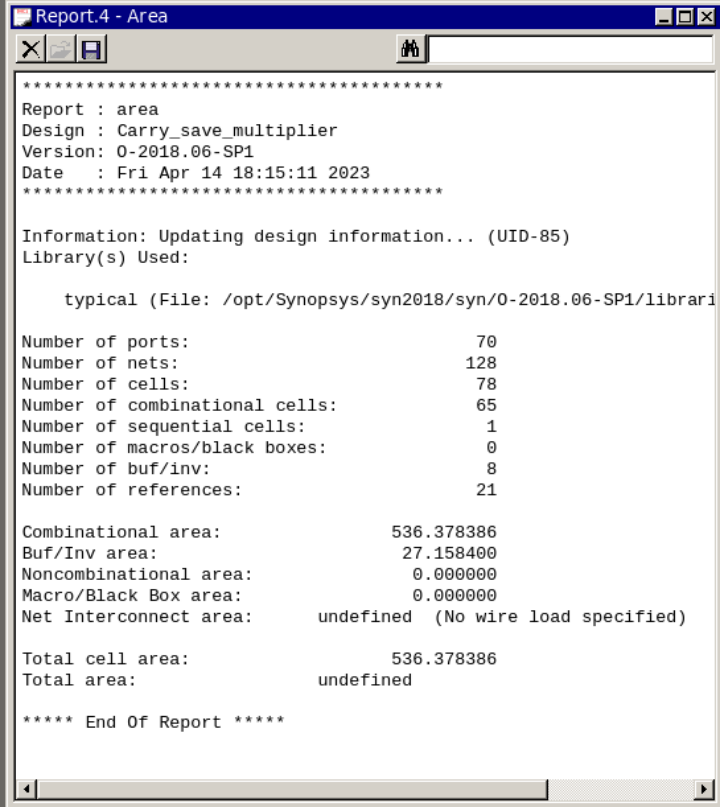
图7 面积报告

进位保留乘法器的Verilog代码如下所示。

module Carry_save_multiplier(input [3:0]A,B,output[7:0]Sum);
    wire [3:0]partial_product[3:0];
    //产生部分积
    assign partial_product[0]=B[0]?A:0;
    assign partial_product[1]=B[1]?A:0;
    assign partial_product[2]=B[2]?A:0;
    assign partial_product[3]=B[3]?A:0;

    //中间进位
    wire C10,C11,C12,C13;
    wire C20,C21,C22,C23;
    wire C30,C31,C32,C33;

    //中间和
    wire S11,S12,S13;
    wire S21,S22,S23;
    wire S31,S32,S33;
    //第一行加法器
    assign Sum[0]=partial_product[0][0];
    Adder_half Adder_half_0(partial_product[0][1],partial_product[1]    
                            [0],Sum[1],C10);
    Adder_half Adder_half_1(partial_product[0][2],partial_product[1][1],S11,C11);
    Adder_half Adder_half_2(partial_product[0][3],partial_product[1][2],S12,C12);
    Adder_half Adder_half_3(partial_product[1][3],1'b0,S13,C13);

    //第二行乘法器
    Adder Adder_1(S11,partial_product[2][0],C10,Sum[2],C20);
    Adder Adder_2(S12,partial_product[2][1],C11,S21,C21);
    Adder Adder_3(S13,partial_product[2][2],C12,S22,C22);
    Adder_half Adder_half_4(C13,partial_product[2][3],S23,C23);

    //第三行加法器
    Adder Adder_4(S21,partial_product[3][0],C20,Sum[3],C30);
    Adder Adder_5(S22,partial_product[3][1],C21,S31,C31);
    Adder Adder_6(S23,partial_product[3][2],C22,S32,C32);
    Adder_half Adder_half_5(C23,partial_product[3][3],S33,C33);

    //向量合并加法器
    assign Sum[7:4]={C33,S33,S32,S31}+{1'b0,C32,C31,C30};


endmodule

module Adder (
    input  Mult1,
    input  Mult2,
    input  I_carry,
    output Res,
    output Carry
);
 
    assign Res = Mult1 ^ Mult2 ^ I_carry;
    assign Carry = (Mult1 & Mult2) | ((Mult1 ^ Mult2) & I_carry);
 
endmodule
 
module Adder_half (
    input  Mult1,
    input  Mult2,
    output Res,
    output Carry
);
 
    assign Res = Mult1 ^ Mult2;
    assign Carry = Mult1 & Mult2;
endmodule

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1057765.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！