1.1 数组的定义

数组中的是在内存中是连续存储的，内存是由一个个内存单元组成的，每一个内存单元都有自己的地址，数组中的每一个元素可以存储在这一个个内存单元中，使用索引来访问数组中的元素。

1.2 数组的创建

int[] arr = {1,2,3,4};

从上一个小节，不难得出，数组中访问元素时的时间复杂度为$O(1)$

1.3 数组在内存中的情况

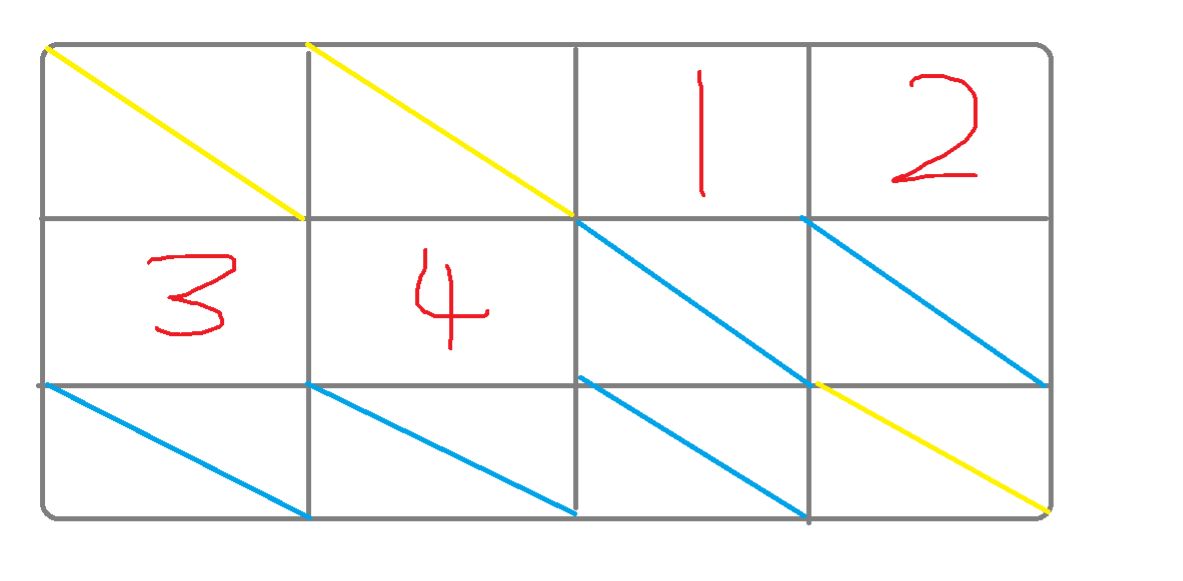
可以理解成图中所示，黄线表示空闲的存储单元，蓝线表示这个存储单元已经被其他元素所占用，1，2，3，4就是所创建的数组，可以看到是连续的。

2.1 初始化数组

 	// 当前数组的元素个数
    private int size = 0;
    // 容量
    private int capacity = 5;
    // 数组
    private int[] array = {};


    /**
     * 数组扩容与初始化数组
     */
    private void checkAndGrow() {
        if (size == 0){ // 如果元素个数为0，就初始化数组
            array = new int[capacity];
        }
        else if (size == capacity) { // 数组已满，就扩容数组
            capacity += capacity >> 1;
            int[] newArray = new int[capacity];
            System.arraycopy(array, 0, newArray, 0, size);
            array = newArray;
        }
    }

时间复杂度为：$O(n)$

2.2 插入元素

    /**
     * 向[0..size]位置添加元素
     *
     * @param index
     * @param element
     */
    public void add(int index, int element) {
        // 检查是否扩容
        checkAndGrow();
        if (index >= 0 && index < size) {
            // 当插入新元素时，其他数组中的元素往右移
            System.arraycopy(array, index, array, index + 1, size - index);
        }

        // 当等于size时插入尾节点
        array[index] = element;
        size++;
    }

    /**
     * 向最后位置[size]添加元素
     *
     * @param element
     */
    public void addLast(int element) {
        add(size, element);
    }

时间复杂度为：$O(n)$

2.3 删除元素

/**
     * 删除数组中的元素
     *
     * @param index
     * @return
     */
    public int remove(int index) {
        int removed = array[index];
        // 当为数组中的最后一个元素，就不需要移动
        if (index < size - 1) {
            System.arraycopy(array, index + 1, array, index, size - index - 1);
        }
        size--;
        return removed;
    }

时间复杂度为：$O(n)$

2.4 读取元素

    /**
     * 根据索引返回元素
     */
    public int get(int index) {
        return array[index];
    }

时间复杂度：$O(1)$

2.5 遍历数组

 /**
     * 基于函数式接口，可以按照要求来指定所要实现的功能
     *
     * @param consumer
     */
    public void myForEach(Consumer<Integer> consumer) {
        for (int i = 0; i < size; i++) {
            consumer.accept(array[i]);
        }
    }


    /**
     * 迭代器遍历
     *
     * @return
     */
    @Override
    public Iterator<Integer> iterator() {
        return new Iterator<Integer>() {
            int i = 0;
            // 查看还是否有下个元素
            @Override
            public boolean hasNext() {
                return i < size;
            }

            // 返回当前所指向的元素，并且指针往后移动
            @Override
            public Integer next() {
                return array[i++];
            }
        };
    }

时间复杂度：$O(n)$