309.最佳买卖股票时机含冷冻期

Leetcode

思路

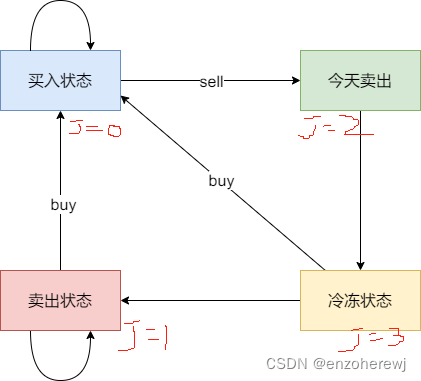
因为有冷静期，我们可以区分出如下的四个状态：

1. dp数组含义

• 状态一(j = 0)：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
• 不持有股票状态，这里就有两种卖出股票状态
  • 状态二(j = 1)：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）可以买入
  • 状态三(j = 2)：今天卖出股票 不可买入
• 状态四(j = 3)：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

2. 递推公式

   根据上图可以得到以下推导公式：

   • dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i])
   • dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
   • dp[i][2] = dp[i - 1][0] + prices[i]
   • dp[i][3] = dp[i - 1][2]

3. 初始化
   如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。其他的状态由递推公式推得为0。

4. 遍历顺序
   从前往后

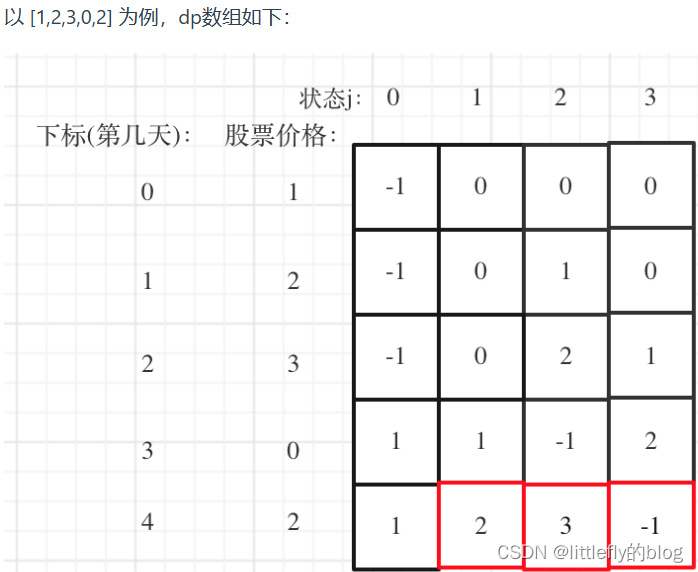
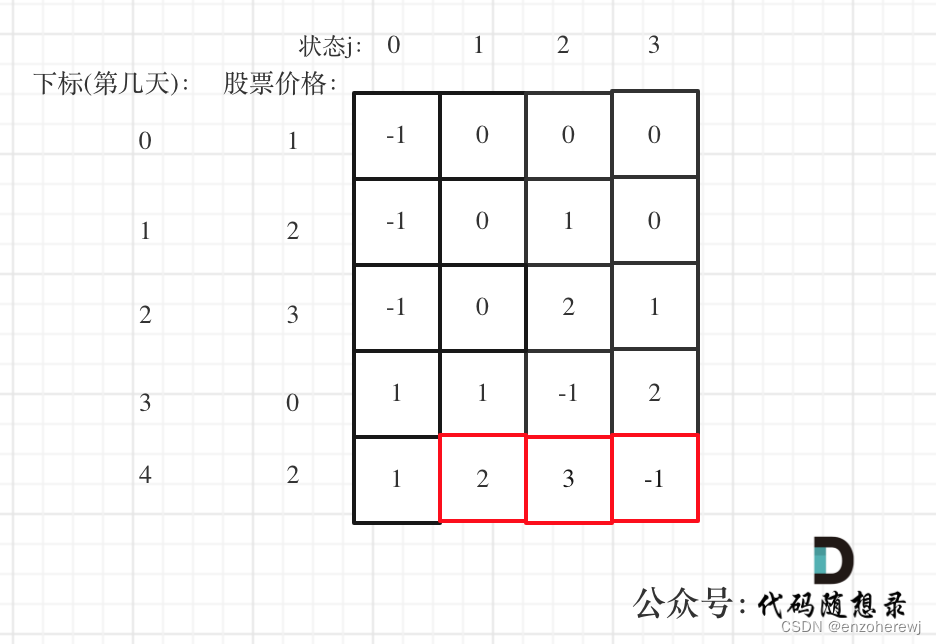
5. 举例推导dp数组
   以 [1,2,3,0,2] 为例，dp数组如下：
   

代码

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        dp = [[0] * 4 for _ in range(n)]

        dp[0][0] = -prices[0]
        for i in range(1, n):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i])
            dp[i][1] = max(dp[i - 1][3], dp[i - 1][1])
            dp[i][2] = dp[i - 1][0] + prices[i]
            dp[i][3] = dp[i - 1][2]

        return max(dp[-1][1], dp[-1][2], dp[-1][3])

• 时间复杂度：O(n)
• 空间复杂度：O(n)

714.买卖股票的最佳时机含手续费

Leetcode

思路

本题的思路和买卖股票ii类似。可以无限次交易，只不过有手续费。

手续费体现的区别就在递推公式上，我们只需要在买入股票的时候减去手续费即可。

dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金。

dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee)

代码

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        n = len(prices)
        dp = [[0] * 2 for _ in range(n)]

        dp[0][0] = -prices[0] - fee

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i] - fee)
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])

        return dp[-1][1]

• 时间复杂度：O(n)
• 空间复杂度：O(n)