一、说明
多项逻辑回归是一种统计方法,用于预测两个以上类别的分类结果。当因变量是分类变量而不是连续变量时,它特别有用。
二、分类预测
在多项式逻辑回归中,模型预测属于因变量每个类别的观测值的概率。这些概率可以解释为观察结果属于每个类别的可能性。预测的类别通常是概率最高的类别,使其成为分类预测而不是连续预测。
相反,当因变量仅具有两个类别时,使用标准逻辑回归,也称为二元逻辑回归(二项式逻辑回归的一种特殊情况) 。它预测观察结果属于一个类别与另一个类别的概率。二元逻辑回归中的预测是0和之间的连续概率1。
三、下层原理
以下是多项逻辑回归背后的数学原理。这些方程表示一组对数线性模型,其中每个类别的概率之比的对数通过系数(或斜率)参数与预测变量 线性相关,用
、
表示。符号
表示观测值
属于
类的概率,其中
是每个类的整数表示,从 1 开始。
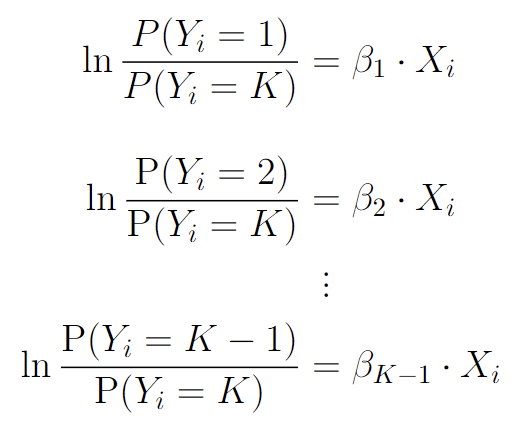
从这些方程中,我们可以简化为下面的方程,它们是我们之前看到的方程的替代形式。它们源自以下事实:所有K个类别的概率之和必须为 1。在这些方程中,分子用作参考类别,其他K – 1 个类别的概率使用指数相对于该参考类别来表示预测变量Xi和相应系数βk的函数。
这些方程中的指数函数 $e$ 用于将线性预测变量(即βk • Xi)转换为概率,该概率始终为正且介于 0 和 1 之间。通过将指数函数e应用于先前的两侧方程,我们得到第一类的以下方程:

这些方程通常用于多项逻辑回归,其目标是基于一个或多个预测变量来预测属于K个类别中每一类的观测值的概率。
四、关于数据
在此示例中,我们将使用加州大学欧文分校的鲍鱼数据集来预测鲍鱼的性别。多元线性回归模型可用于预测年龄,但在本例中,我们根据几个不同的特征来预测给定鲍鱼的性别。
使用Python pandas包,我们可以看到数据的形状,以及前几行。
import pandas as pd df = pd.read_csv("https://raw.githubusercontent.com/s-lasch/CIS-280/main/abalone.csv") # read csv df.shape # get shape(4177, 9)df.head() # show first 5 rows| sex | length | diameter | height | whole_weight | shucked_weight | viscera_weight | shell_weight | rings |
------------------------------------------------------------------------------------------------------------
| M | 0.455 | 0.365 | 0.095 | 0.5140 | 0.2245 | 0.1010 |0.150 | 15 |
| M | 0.350 | 0.265 | 0.090 | 0.2255 | 0.0995 | 0.0485 | 0.070 | 7 |
| F | 0.530 | 0.420 | 0.135 | 0.6770 | 0.2565 | 0.1415 | 0.210 | 9 |
| M | 0.440 | 0.365 | 0.125 | 0.5160 | 0.2155 | 0.1140 | 0.155 | 10 |
| I | 0.330 | 0.255 | 0.080 | 0.2050 | 0.0895 | 0.0395 | 0.055 | 7 |五、处理数据
我们可以看到该列中有三个不同的类别sex:M、F 和 I,分别代表男性、女性和婴儿。这些代表我们的模型将根据数据集中的其他列预测的类。
df['sex'].value_counts().sort_values(ascending=False) # count the number of distinct classesM 1528
I 1342
F 1307
Name: sex, dtype: int64 这意味着我们的y数据将是sex列,而我们的X数据将是除 之外的所有列sex。
X = df.drop(['sex'], axis=1)
y = df['sex']现在我们准备将数据分为训练和测试。我们可以使用scikitlearn如下所示的包来做到这一点:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 5)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)(3341, 8)
(836, 8)
(3341,)
(836,)六、一次性编码
现在我们有了训练和测试数据,重要的是要记住任何回归模型都需要整数或浮点输入。由于该sex列是分类列,因此我们需要应用整数编码才能将它们用于回归。为此,我们将应用one-hot 编码,它将为每个不同的类分配一个整数。
y_train = y_train.apply(lambda x: 0 if x == "M" else 1 if x == "F" else 2)
y_test = y_test.apply(lambda x: 0 if x == "M" else 1 if x == "F" else 2) 现在y数据已编码,我们必须将每个训练/测试数据集转换为torch.tensor. 这对于使用 Pytorch 的任何回归至关重要,因为它只能采用张量。
X_train_tensor = torch.tensor(X_train.to_numpy()).float()
X_test_tensor = torch.tensor(X_test.to_numpy()).float()
y_train_tensor = torch.tensor(y_train.to_numpy()).long()
y_test_tensor = torch.tensor(y_test.to_numpy()).long()有关张量的更多信息,可以在这里找到真正深入的资源。史蒂文·拉什
七、该模型
数据处理完成后,我们现在可以开始创建模型的过程。为了实现这个模型,我们将使用 Pytorch 库。由于有 8 个特征用于确定性别,因此我们需要将 设为in_features8。由于模型只能预测三种可能的类别,因此out_features将设为 3。有关 Pytorchtorch.nn模块的更多信息,请参阅文档。
import torch
import torch.nn as nn
from torch.nn import Linear
import torch.nn.functional as F
torch.manual_seed(348965) # keep random values consistent
model = Linear(in_features=8, out_features=3) # define the model
# define the loss function and optimizer
criterion = nn.CrossEntropyLoss() # use cross-entropy loss for multi-class classification
optimizer = torch.optim.SGD(model.parameters(), lr=.01) # learning rate of 0.01, and Stocastic Gradient descent optimizer八、训练模型
num_epochs = 2500 # loop iterations
for epoch in range(num_epochs):
# forward pass
outputs = model(X_train_tensor)
loss = criterion(outputs, y_train_tensor)
# backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print progress every 100 epochs
if (epoch+1) % 100 == 0:
print('Epoch [{}/{}]\tLoss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))Epoch [100/2500] Loss: 1.1178
Epoch [200/2500] Loss: 1.1006
Epoch [300/2500] Loss: 1.0850
Epoch [400/2500] Loss: 1.0708
Epoch [500/2500] Loss: 1.0579
Epoch [600/2500] Loss: 1.0460
Epoch [700/2500] Loss: 1.0352
Epoch [800/2500] Loss: 1.0252
Epoch [900/2500] Loss: 1.0161
Epoch [1000/2500] Loss: 1.0077
Epoch [1100/2500] Loss: 0.9999
Epoch [1200/2500] Loss: 0.9927
Epoch [1300/2500] Loss: 0.9860
Epoch [1400/2500] Loss: 0.9799
Epoch [1500/2500] Loss: 0.9741
Epoch [1600/2500] Loss: 0.9688
Epoch [1700/2500] Loss: 0.9638
Epoch [1800/2500] Loss: 0.9592
Epoch [1900/2500] Loss: 0.9549
Epoch [2000/2500] Loss: 0.9509
Epoch [2100/2500] Loss: 0.9471
Epoch [2200/2500] Loss: 0.9435
Epoch [2300/2500] Loss: 0.9402
Epoch [2400/2500] Loss: 0.9371
Epoch [2500/2500] Loss: 0.9342九、验证
现在要检查准确性,我们可以运行以下代码:
outputs = model(X_test_tensor)
_, preds = torch.max(outputs, dim=1)
accuracy = torch.mean((preds == y_test_tensor).float())
print('\nAccuracy: {:.2f}%'.format(accuracy.item()*100))Accuracy: 52.63%这意味着我们的模型在几乎 53% 的时间内根据 8 个不同特征准确识别了鲍鱼的性别,这不是很好。
十、完整代码
这是完整的代码:
import torch
import torch.nn as nn
from torch.nn import Linear
import torch.nn.functional as F
torch.manual_seed(348965) # keep random values consistent
model = Linear(in_features=8, out_features=3) # define the model
# define the loss function and optimizer
criterion = nn.CrossEntropyLoss() # use cross-entropy loss for multi-class classification
optimizer = torch.optim.SGD(model.parameters(), lr=.01) # learning rate of 0.01, and Stocastic Gradient descent optimizer
# convert the data to PyTorch tensors
X_train_tensor = torch.tensor(X_train.to_numpy()).float()
X_test_tensor = torch.tensor(X_test.to_numpy()).float()
y_train_tensor = torch.tensor(y_train.to_numpy()).long()
y_test_tensor = torch.tensor(y_test.to_numpy()).long()
# train the model
num_epochs = 2500 # loop iterations
for epoch in range(num_epochs):
# forward pass
outputs = model(X_train_tensor)
loss = criterion(outputs, y_train_tensor)
# backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print progress every 100 epochs
if (epoch+1) % 100 == 0:
print('Epoch [{}/{}]\tLoss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))
outputs = model(X_test_tensor)
_, preds = torch.max(outputs, dim=1)
accuracy = torch.mean((preds == y_test_tensor).float())
print('\nAccuracy: {:.2f}%'.format(accuracy.item()*100))Epoch [100/2500] Loss: 1.1178
Epoch [200/2500] Loss: 1.1006
Epoch [300/2500] Loss: 1.0850
Epoch [400/2500] Loss: 1.0708
Epoch [500/2500] Loss: 1.0579
Epoch [600/2500] Loss: 1.0460
Epoch [700/2500] Loss: 1.0352
Epoch [800/2500] Loss: 1.0252
Epoch [900/2500] Loss: 1.0161
Epoch [1000/2500] Loss: 1.0077
Epoch [1100/2500] Loss: 0.9999
Epoch [1200/2500] Loss: 0.9927
Epoch [1300/2500] Loss: 0.9860
Epoch [1400/2500] Loss: 0.9799
Epoch [1500/2500] Loss: 0.9741
Epoch [1600/2500] Loss: 0.9688
Epoch [1700/2500] Loss: 0.9638
Epoch [1800/2500] Loss: 0.9592
Epoch [1900/2500] Loss: 0.9549
Epoch [2000/2500] Loss: 0.9509
Epoch [2100/2500] Loss: 0.9471
Epoch [2200/2500] Loss: 0.9435
Epoch [2300/2500] Loss: 0.9402
Epoch [2400/2500] Loss: 0.9371
Epoch [2500/2500] Loss: 0.9342最初于 2023 年 5 月 1 日发布于https://s-lasch.github.io。