概要
贝叶斯定理描述的是条件概率,不同于全局概率,它表示当某一个事件(B)发生时,另一个事件(A)发生的概率。从机器学习的角度,从全局无法知道事件(A)发生的概率,但是如果能确认一些事情发生,如事件(B),那么就可以更新事件(A)发生的概率,从而逼近真实值。
基础知识
概率 -- 一件事发生的概率等于该事件发生的数目除以所有事件发生的数目,P(A);
条件概率 -- 一件事在特定条件下发生的概率,P(A|B)。如“假如我知道一个人是女士,那么她留长发的概率是多少”。这里B表示女士,A表示长头发;另外P(A|B)!= P(B|A),比如,P(cute | puppy) 是不一样的 P(puppy | cute)。如果我抱着是小狗,那么它可爱的概率就很高,如果我抱着的东西很可爱,那么它是小狗的概率就可能很低,因为它可能是小猫、兔子、刺猬或者是一个小宝宝;
联合概率 – 两件事同时发生的概率,P(A and B) = P(A) * P(B|A)。注意P(A and B) != P(A) * P(B)。原因是前者考虑了两件事的相关性,而后者没有。举个例子,如果A和B发生的概率都是50%,但两者是强相关的,A出现时B必然出现,那么P(A and B)=50%;反之如果A出现时B必然不会出现,那么P(A and B)=0;
边际概率 -- 即相对多变量的联合分布而言,当其他变量取一切可能,某变量取值的概率。边际概率是一个事件的概率,与另一个变量的结果无关。 我们可以从后文的公式中再体会边际概率的含义。
公式
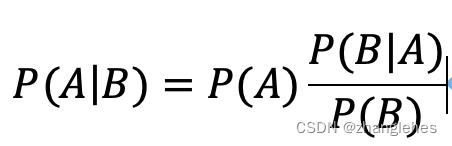
P(A|B) – 条件概率,同时也是后验概率,它表示当事件B发生后,对于发生事件A的概率修正;
P(A) – 初始概率,同时也是前验概率,它可能是一个准确值,也可能表示我们对事件A发生的估计概率;
P(B|A) – 它也是个条件概率,在贝叶斯应用中,它是一个容易求得的值;
P(B) – 边缘概率
公式变换
贝叶斯公式有很多表现形式,适用于不同的应用场景。在这里我们对边际概率进行细化(根据它的定义)
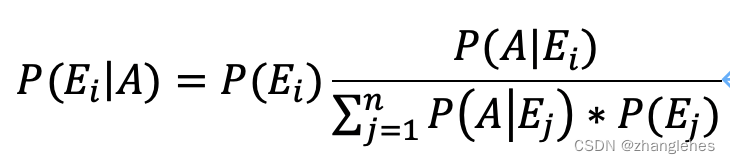
贝叶斯公式的应用场景
- Understanding probability problems (including those in medical research)
- Statistical modelling and inference
- Machine learning algorithms (such as Naive Bayes, Expectation Maximisation)
- Quantitative modelling and forecasting
示例
示例1
第一个盒子有4个红球、2个绿球,第二个盒子有2个红球、4个绿球。假设有1/3的概率从第一个盒子内取球,有2/3的概率从第二个盒子内取球。随机从任意一个盒子内取任意一个球:
- 如果取到的球是红色的,那么有多大概率来至第一个盒子?
- 如果取到的球是红色的,那么有多大概率来至第二个盒子?
- 对比一下前两问的答案,并解释原因
解答1: 假设从第一个盒子取球的事件为E1,则P(E1) = 1/3,假设从第二个盒子取球的事件为E2,则P(E2) = 1/3。从第一个盒子取到红球的概率P(R|E1)=2/3,从第二个盒子取到红球的概率P(R|E2)=1/3。问题是求解P(E1|R),按照公式
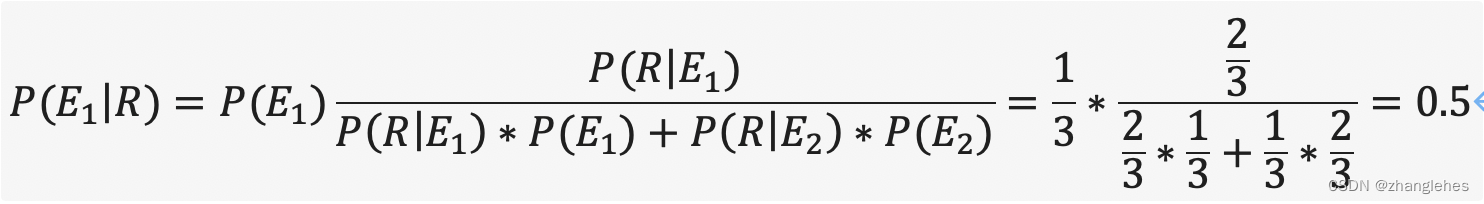
解答2:

解答3:两问的答案相同,原因是贝叶斯公式同时考虑了选择某个盒子的概率,和从特定盒子中选择红球的概率。
示例2
有一种疾病,1%的人群会感染上。医疗上检测该疾病,在得病的人群中有95%的几率能检测出,同时也有%2的几率在未感染的人群中检测出。如果一个人被检测出得该疾病,那么他真实获病得几率是多少?
解答:假设真实得病的事件为D,那么P(D)=1%,P(~D)=99%。检测出疾病的事件为E,那么P(E|D)=95%,P(E|~D)=2%。问题是P(D|E)
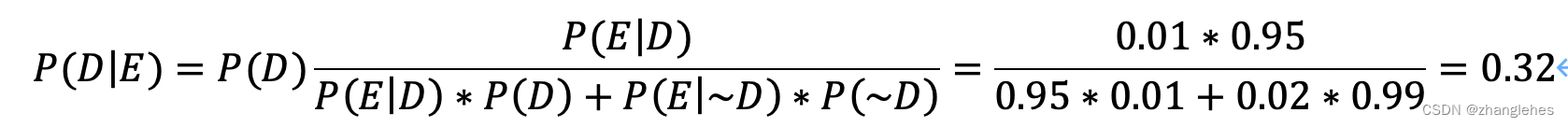
由此可见,即使被检测出疾病,真实获病的概率其实并不高。原因是前验概率非常低,同时检测误差却相对较高。
示例3
市场上有3个工厂(A,B,C)生产灯泡,它们的市场占有率分别是20%,50%和30%。其对应的缺陷产品率分别是2%,1%,3%。如果有一个缺陷灯泡被检测到了,那么它来自于B工厂的概率是多少?
解答:首先P(A)=20%, P(B)=50%, P(C)=30%,另一个条件,假设缺陷产品的事件为D,则P(D|A)=2%, P(D|B)=1%, P(D|C)=3%, 问题是P(B|D)

由此可见,虽然B工厂的市场占有率较高,但是因为其产品缺陷率较低,导致问题产品来自于它生产的灯泡的概率也不高。
示例4
有一套雷达系统,当飞机在它的监控范围时,它有98%的概率能监测出来。但是当无飞机时,仍有5%的概率能监测出来。在任意时间,该空域出现飞机的概率是7%。
- 当雷达监测出飞机时,有多大概率无飞机存在?
- 当雷达监测出飞机时,有多大概率有飞机存在?
- 当雷达未监测出飞机时,有多大概率有飞机存在?
- 当雷达未监测出飞机时,有多大概率无飞机存在?
解答:飞机出现在该空域的时间为M,则P(M)=7%,P(~M)=93%。另一个条件,监测出飞机的事件为D,P(D|M)=98,P(D|~M)=5%。
- P(~M|D)=(0.93*0.05)/(0.93*0.05+0.98*0.07) = 0.404
- P(M|D)=(0.07*0.98)/(0.93*0.05+0.98*0.07) = 0.596
- 这里需要做一个转换,P(~D|M) = 1-P(D|M)和P(~D|~M) = 1-P(D|~M)。则P(M|~D)=0.0016
- P(~M|~D)=0.9984
参考文献
- 贝叶斯推理原理 - 知乎
- Bayes' Rule – Explained For Beginners
- Bayes Theorem Explained With Example - Complete Guide | upGrad blog
- https://www.analyzemath.com/probabilities/bayes-theorem.html