全面解读 SQL 优化

一、简介

数据库中的优化器（optimizer）是一个重要的组件，用于分析 SQL 查询语句，并生成执行计划。在生成执行计划时，优化器需要依赖数据库中的统计信息来估算查询的成本，从而选择最优的执行计划。以下是关于数据库中优化器统计信息的简介：

（1）统计信息概述

统计信息是描述表或索引中数据分布情况的元数据。这些信息包括行数、数据分布、重复值等，都是优化器选择执行计划的关键因素。

（2）统计信息来源

统计信息被收集并存储在数据字典中，可以通过特定的 SQL 命令（如 ANALYZE TABLE）来手动收集；也可以被自动收集，以保持数据字典的最新状态。

（3）统计信息类型

统计信息包括两种不同类型的信息，系统级别和对象级别。系统级别的统计信息是全局性的，如整个数据库中所有表的平均行长度；而对象级别的统计信息是特定对象的信息，如表或索引的平均行长度、列值的分布和直方图等。

（4）统计信息用途

优化器使用统计信息作为计算成本的基础，从而选择最优执行计划。优化器所使用的统计信息包括表的行数、每个列的唯一值数目、平均列长度等。

（5）统计信息更新

数据的分布会随着时间和数据量的增长而发生变化，因此统计信息也需要定期更新。更新统计信息的频率取决于表中数据的变化速度和查询的要求。

总之，优化器统计信息是一个关键的组件，用于执行计划的生成和执行。数据库管理员需要定期维护和更新统计信息，以支持数据库的正常运行和高效执行 SQL 查询。

目前 KaiwuDB 维护的统计信息包括表和列的统计信息，这是本期技术贴重点介绍的内容。

➢ 表的统计信息：总行数；

➢ 列的统计信息：不同值的数目，NULL 值的数目和直方图。

二、统计信息流程

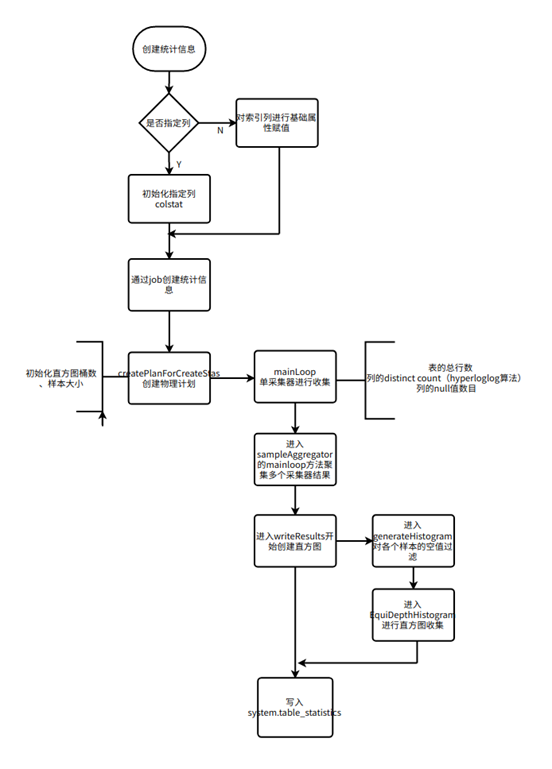
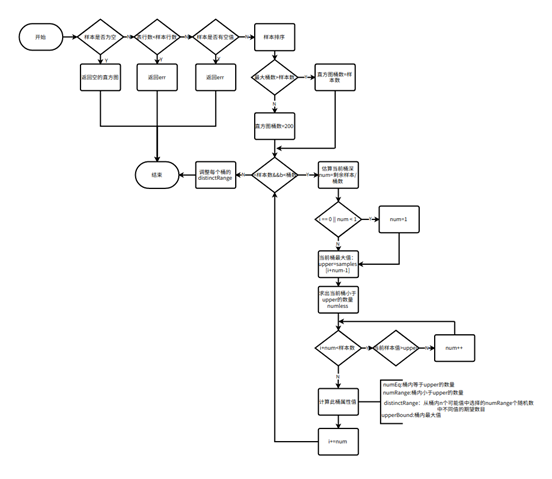
生成统计信息的简单流程如图所示，详细采样过程由后文部分介绍。

Sampler（"采样器"处理器的规范）

该处理器返回输入列的样本(随机子集)并计算列集上的基数估计草图。

SampleAggregator（处理器的规范）

该处理器聚合来自多个采样器处理器的结果，并将统计信息写到 system.table_statistics 中。

三、基数统计算法

HyperLogLog 是一种基数（cardinality）估计算法，用于在海量数据中估计不同元素的数量。该算法使用了概率技巧和哈希函数，可以在极大数据量下高效地统计基数。以下是关于 HyperLogLog 的简介：

基数（cardinality）

基数是指集合中不同元素的数量。例如，在某个网站上的用户访问记录中，基数表示的是不同的用户数量；

精确计数局限

对于大规模数据，精确计算基数的代价会非常昂贵，因为需要遍历整个数据集，消耗大量计算资源和时间；

算法原理

HyperLogLog 利用了哈希函数和概率的原理，将输入的元素通过哈希函数映射到一个固定大小的二进制空间，并计算这些哈希值的最大前缀 0 的位数。然后，将这些最大前缀 0 的位数的平均值作为基数的估计值；

精度控制

HyperLogLog 的精度受哈希函数的影响，可以通过调整哈希函数的参数来控制精度。一般来说，HyperLogLog 算法可以在仅占原始数据 1-2% 的空间下，对基数进行非常准确的估计，误差通常在 1% 以内；

应用场景

HyperLogLog 广泛应用于大规模数据的基数统计，如页面访问、IP 地址统计、社交网络中用户数量估算等。

总之，HyperLogLog 算法是一种高效的基数统计算法，可以在大规模数据下进行快速而准确的基数估计，具有广泛的应用前景，以下将为大家介绍 KaiwuDB 是如何进行实现的。

主要计算：2 的第一个 0 出现位置次方的调和平均值

1. 算法步骤

（1）转化为比特串

通过哈希函数，将输入的数据转化为 64 位比特串，哈希函数将 2^64 个不同值映射到 0~2^64-1 地址上。比特串中的 0 和 1 可以类比为硬币的正与反，这是实现估值统计的第一步；

（2）分桶平均

首先初始化数据结构 sketch，包括分桶数、修正系数等。然后将每个元素的 hash 值取最后的 p 位决定桶的编号，在剩余的（64-p）位中找到最大的第一个"0"出现的位置；

（3）计算调和平均数

所有元素处理完毕后，求所有桶中值的调和平均数即可得到 distinct 值。

2. 估算流程

HyperLogLog 是 KaiwuDB 统计信息中计算 Distinct 值的主要估计算法。下图为详细流程：

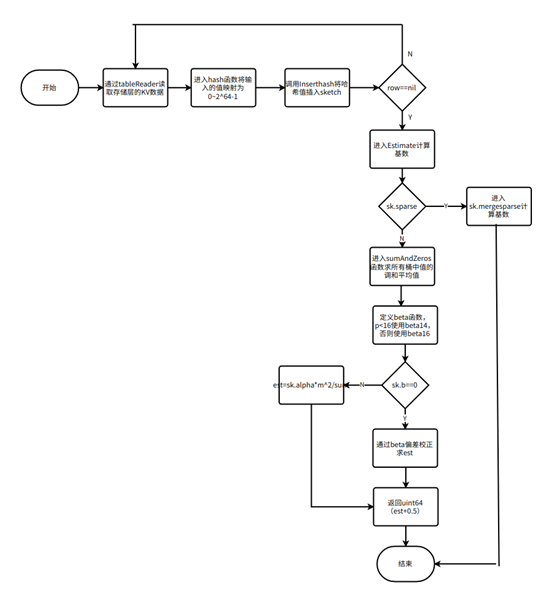
3. 算法优势

利用尽可能少的内存空间实现大数据集的基数统计。

2^14桶

Go
root@:26257/defaultdb> select count(*) from t1;
  count
---------
  10000
(1 row)

Time: 3.300613ms

root@:26257/defaultdb> Show statistics for table t1;
  statistics_name | column_names |             created              | row_count | distinct_count | null_count |    histogram_id
------------------+--------------+----------------------------------+-----------+----------------+------------+---------------------
  t1s             | {c1}         | 2023-05-28 00:53:09.573502+00:00 |     10000 |           9920 |          0 | 868891982501675009
(1 row)

Time: 2.021244ms

2^16桶

Go
root@:26257/defaultdb> select count(*) from t1;
  count
---------
  10000
(1 row)

Time: 4.210306ms

root@:26257/defaultdb>  Show statistics for table t1;
  statistics_name | column_names |             created              | row_count | distinct_count | null_count |    histogram_id
------------------+--------------+----------------------------------+-----------+----------------+------------+---------------------
  t1s             | {c1}         | 2023-05-28 01:02:29.997638+00:00 |     10000 |           9999 |          0 | 868893818901430273
(1 row)

Time: 3.056793ms

桶的个数越多，HyperLogLog 的精度就越高，同时所占用的内存也越大。

四、蓄水池算法

蓄水池算法（Reservoir Sampling）是一种在数据流中随机采样的算法，常用于生成一个固定大小的随机样本。以下是关于蓄水池算法的介绍：

（1）数据流

在大规模数据处理中，数据通常以数据流的形式出现，即数据无法事先被全部存储下来，而必须通过流式处理方式来逐个处理；

（2）算法原理

蓄水池算法需要维护一个大小为 k 的蓄水池，初始时将前 k 个元素放入蓄水池中，然后对于第 i 个元素，有 1/i 的概率将其替换蓄水池中的任意一个元素；

（3）采样理论

根据采样理论，该算法可以保证每个元素被采样的概率都相等，即 1/n，其中 n 为数据流中元素的数量；

（4）应用场景

蓄水池算法广泛应用于随机采样问题，如从海量数据中随机选取 k 个元素进行分析、从实时日志数据中随机选取一部分数据进行监控等；

（5）算法优点

蓄水池算法具有高效、可扩展、精度高等优点，并且能够在空间与时间复杂度上做到线性级别。

总之，蓄水池算法是一种高效的随机采样算法，可以在数据流中进行随机采样，并保证每个元素被选中的概率都相等，具有广泛的应用前景，以下内容为蓄水池算法在 KaiwuDB 中的实现流程。

在 mainloop 函数中通过蓄水池抽样算法，来生成均匀抽样集合。

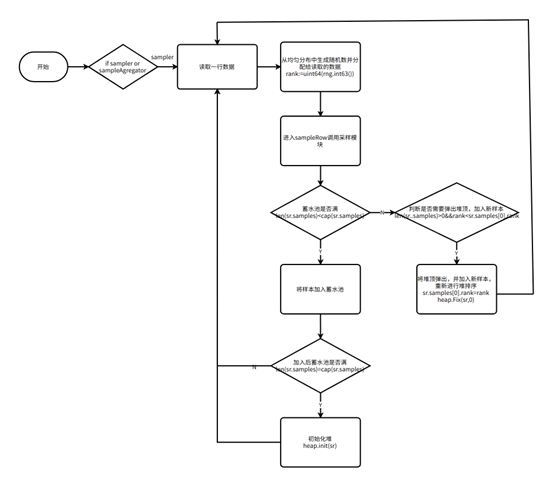
采样过程的 processor 有 sampler 和 sampleaggregator 都采用了采样模块。

其中 sampler processor 的输入为 tablereader 下读取到的数据，是未经任何采样的数据；sampleaggregator processor 输入为各个 sampler processor 的取样结果，是经过采样的数据。

五、直方图计算流程

直方图是一个描述数据分布情况的工具，KaiwuDB 采用等深直方图。

根据采样得到的样本进行直方图的创建，创建方法大致如下(详情参考EquiDepthHistogram函数)：

将样本排序，顺序遍历每一个值 V：

如果 V 等于上一个值，那么把 V 放在与上一个值相同的一个桶里，无论桶是不是已经满，这样可以保证每个值只存在于一个桶中；
如果 V 不等于上一个值，那么需要判断当前桶是否已经满，如果不是的话，就直接放入当前桶；否则，就放入下一个桶。

创建完毕，在函数 writeResults 中将结果存储在 system.table_statistics 中。

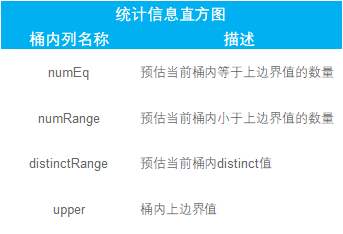
六、应用统计信息计算选择率

选择率表示一个查询根据谓词选择出元组的占比，主要用于优化器预估选择的元组的大小，从而进一步选择出最优的执行计划。

主要流程：当一个过滤条件输入进来时，根据其谓词表达式判断对应的列适用于哪些过滤率的计算方式，然后根据收集到的统计信息与计算方式相结合，得到最终的过滤率。

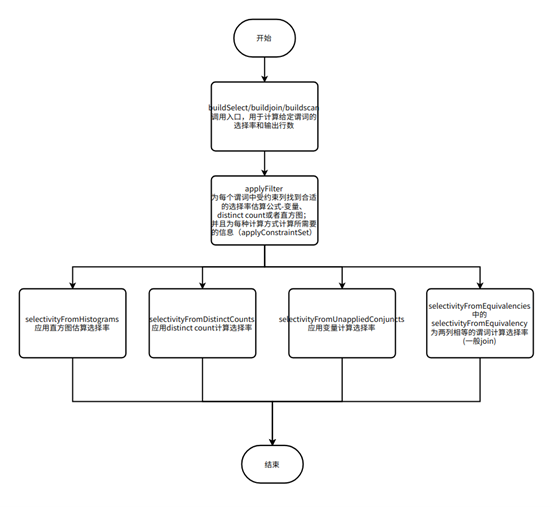
应用直方图和 distinct count 为每个列应用过滤的公式：

SQL
selectivity = (output row count) / (input row count)
其中：
output row count = nonNullSelectivity*输入的非空值数量  + nullSelectivity*输入空值数量
input row count：该列总行数
nonNullSelectivity：桶过滤后的非空值行数/桶过滤前的非空值的行数
nullSelectivity：过滤前后空值的占比