pytorch入门篇

文章目录

张量
- 张量的创建
- - 直接创建
  - 依据数值创建
  - 依概率分布创建张量
- 张量的操作
- - 张量的拼接与切分
  - 张量索引
  - 张量变换
- 线性回归模型
神经网络
- softmax
- softmax实现
- 自动求导
- transforms方法
迁移学习
保存和加载模型

张量

张量（Tensors）类似于NumPy的ndarrays，但张量可以在GPU上进行计算。所以从本质上来说，PyTorch是一yi个处理张量的库。一个张量是一个数字、向量、矩阵或任何n维数组。

张量的创建

直接创建

torch.tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False)

data: 数据，可以是list，numpy
dtype: 数据类型，默认与data的一致
device: 所在设备，cuda/cpu
requires_grad: 是否需要梯度
pin_memory: 是否存于锁页内存

依据数值创建

torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)
torch.ones(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

size: 张量的形状，如(3, 3)、(3, 224, 224)
out: 输出的张量
layout: 内存中布局形式，有strided, sparse_coo等
device: 所在设备，gpu/cpu
requires_grad: 是否需要梯度

torch.zeros_like(input, dtype=None, layout=None, device=None, requires_grad=False)
torch.ones_like(input, dtype=None, layout=None, device=None, requires_grad=False)

input: 创建与input同形状的全0张量
dtype: 数据类型
layout: 内存中布局形式

torch.full(size, fill_value, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)
torch.full_like(input, dtype=None, layout=torch.strided, device=None, requires_grad=False)

size: 张量的形状，如(3, 3)
fill_value: 张量的值

torch.arange(start=0, end. step=1, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：创建等差的1维张量
start: 数列起始值
end: 数列“结束值”
step: 数列公差，默认为1
注意事项：数值区间为 [start,end)

依概率分布创建张量

torch.normal(mean, std, out=None)

功能：生成正态分布（高斯分布）
mean: 均值
std: 标准差
四种模式：
mean为标量，std为标量
mean为标量，std为张量
mean为张量，std为标量
mean为张量，std为张量

torch.normal(mean, std, size, out=None)

功能：生成一定大小的生成正态分布（高斯分布）

在这里插入图片描述

torch.randn(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：生成标准正态分布
size: 张量的形状

在这里插入图片描述

torch.rand(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：在区间 [0,1) 上，生成均匀分布

在这里插入图片描述

torch.randint(low=0, high, size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：区间 [low,high) 生成整数均匀分布
size：张量的形状

在这里插入图片描述

张量的操作

张量的拼接与切分

torch.cat(tensors, dim=0, out=None)

功能：将张量按维度dim进行拼接
tensors：张量序列
dim：要拼接的维度

在这里插入图片描述

torch.stack(tensors, dim=0, out=None)

功能：在新创建的维度dim上进行拼接
tensors：张量序列
dim：要拼接的维度

torch.split(tensor, split_size_or_sections, dim=0)

返回值：张量列表
tensor：要切分的张量
split_size_or_sections：为int时，表示每一份的长度；为list时，按list元素切分
dim：要切分的维度

在这里插入图片描述

张量索引

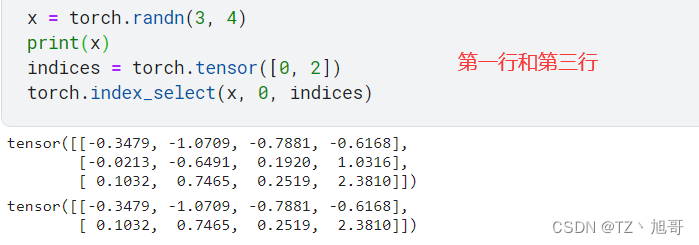
torch.index_select(input, dim, index, out=None)

功能：在维度dim上，按index索引数据
返回值：依index索引数据拼接的张量
index：要索引的张量
dim：要索引的维度
index：要索引数据的序号

在这里插入图片描述

torch.masked_select(input, mask, out=None)

功能：按mask中的True进行索引
返回值：一维张量
input：要索引的张量
mask：与input同形状的布尔类型张量

在这里插入图片描述

张量变换

torch.reshape(input, shape)

功能：变换张量形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存
input：要变换的张量
shape：新张量的形状

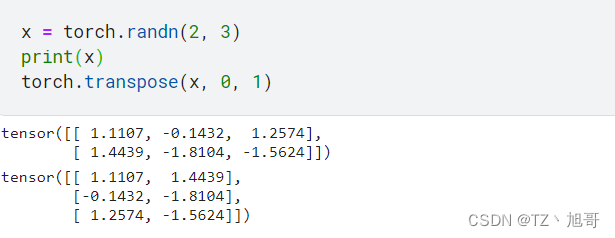
在这里插入图片描述

torch.transpose(input, dim0, dim1)

功能：交换张量的两个维度
input：要交换的张量
dim0：要交换的维度
dim1：要交换的维度

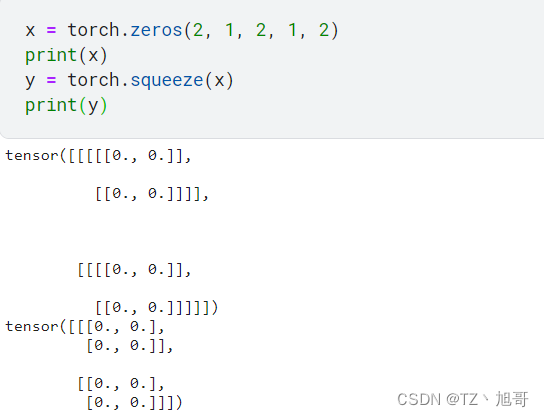
在这里插入图片描述

torch.squeeze(input, dim=None, out=None)

功能：压缩长度为1的维度（轴）
dim：若为None，移除所有长度为1的轴；若指定维度，当且仅当该轴长度为1时，可以被移除

在这里插入图片描述

torch.unsqueeze(input, dim, out=None)

功能：依据dim扩展维度
dim：扩展的维度

在这里插入图片描述

线性回归模型

在这里插入图片描述

# 首先我们得有训练样本X，Y， 这里我们随机生成
x = torch.rand(20, 1) * 10
y = 2 * x + (5 + torch.randn(20, 1))

# 构建线性回归函数的参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)   # 这俩都需要求梯度

# 设置学习率lr为0.1
lr = 0.1

for iteration in range(100):
    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)
 
    # 计算loss
    loss = (0.5 * (y-y_pred)**2).mean()
 
    # 反向传播
    loss.backward()
 
    # 更新参数
    b.data.sub_(lr * b.grad)    # 这种_的加法操作时从自身减，相当于-=
    w.data.sub_(lr * w.grad)

    # 梯度清零
    w.grad.data.zero_()
    b.grad.data.zero_()

print(w.data, b.data)

在这里插入图片描述

神经网络

softmax

在这里插入图片描述

softmax实现

在这里插入图片描述

import torch
from torch import nn

# 确定随机数种子
torch.manual_seed(7)
# 自定义数据集
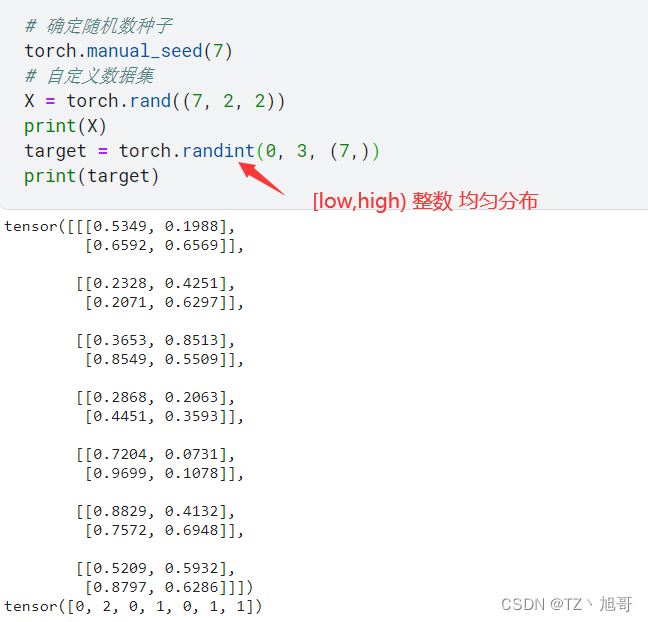
X = torch.rand((7, 2, 2))
print(X)
target = torch.randint(0, 3, (7,))
print(target)


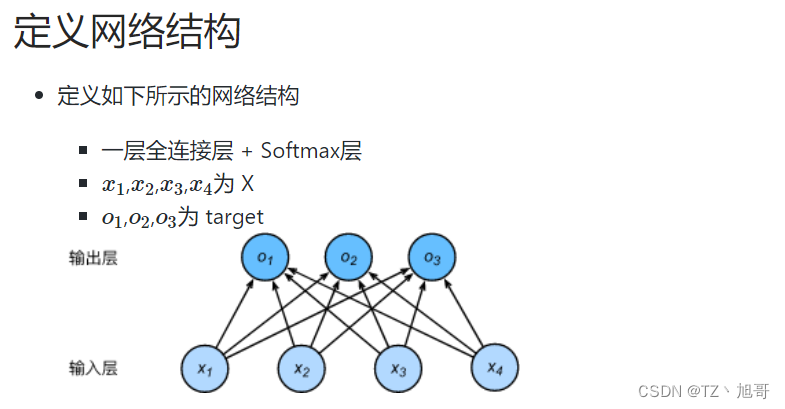
# 自定义网络结构
class LinearNet(nn.Module):
    def __init__(self):
        super(LinearNet, self).__init__()
        # 定义一层全连接层
        self.dense = nn.Linear(4, 3)   # 4 = 2*2  3是target的类别数
        # 定义Softmax
        self.softmax = nn.Softmax(dim=1)

    def forward(self, x):
        y = self.dense(x.view((-1, 4)))   # view 类似于reshape()  -1 表示不确定 自动计算
        y = self.softmax(y)
        return y

net = LinearNet()

loss = nn.CrossEntropyLoss()  # 交叉熵损失函数

optimizer = torch.optim.SGD(net.parameters(), lr=0.1)  # 随机梯度下降法

for epoch in range(70):
    train_l = 0.0
    y_hat = net(X)
    l = loss(y_hat, target).sum()

    # 梯度清零
    optimizer.zero_grad()
    # 自动求导梯度
    l.backward()
    # 利用优化函数调整所有权重参数
    optimizer.step()

    train_l += l
    print('epoch %d, loss %.4f' % (epoch + 1, train_l))

自动求导

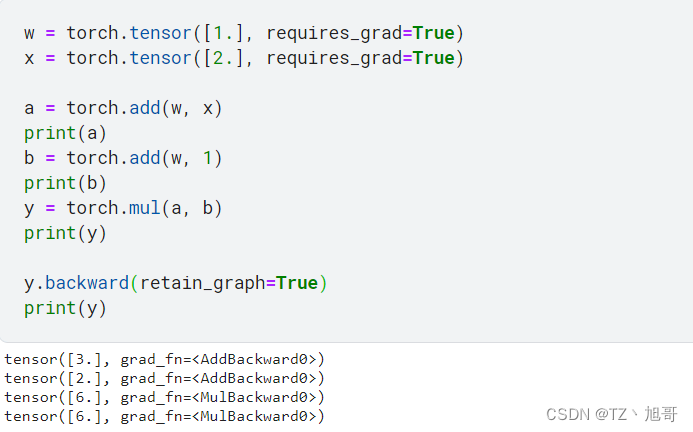
torch.autograd.backward(tensors, grad_tensors=None, retain_graph=None, create_graph=False)

功能：自动求取梯度
tensors：用于求导的张量，如 loss
retain_graph：保存计算图
create_graph：创建导数计算图，用于高阶求导
grad_tensors：多梯度权重

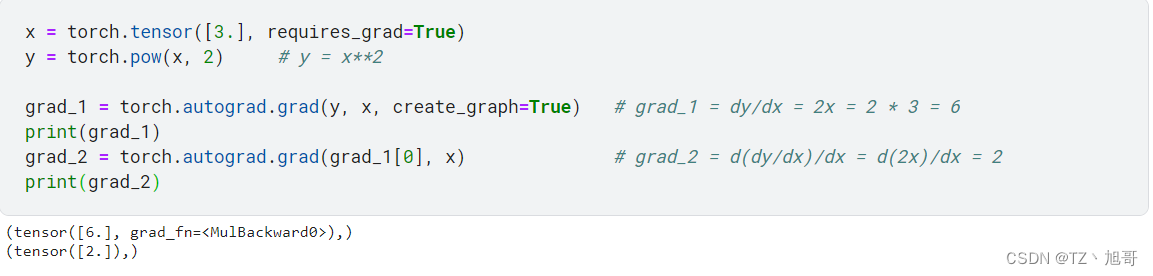
在这里插入图片描述

torch.autograd.grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False)

功能：求取梯度
outputs：用于求导的张量，如 loss
inputs：需要梯度的张量
create_graph：创建导数计算图，用于高阶求导
retain_graph：保存计算图
grad_outputs：多梯度权重

在这里插入图片描述

autograd小贴士：
梯度不自动清零
依赖于叶子节点的节点，requires_grad默认为True
叶子节点不可执行in-place
autograd 包是 PyTorch 中所有神经网络的核心。
首先让我们简要地介绍它，然后我们将会去训练我们的第一个神经网络。该 autograd 软件包为 Tensors 上的所有操作提供自动微分。它是一个由运行定义的框架，这意味着以代码运行方式定义你的后向传播，并且每次迭代都可以不同。
我们从 tensor 和 gradients 来举一些例子。
torch.Tensor是包的核心类。如果将其属性.requires_grad设置为True，则会开始跟踪针对tensor的所有操作。完成计算后，你可以调用.backward()来自动计算所有梯度。该张量的梯度将累积到.grad属性中。
要停止tensor历史记录的跟踪，你可以调用.detach()，它将其与计算历史记录分离，并防止将来的计算被跟踪。
要停止跟踪历史记录（和使用内存），你还可以将代码块使用with torch.no_grad()：包装起来。在评估模型时，这是特别有用，因为模型在训练阶段具有requires_grad=True的可训练参数有利于调参，但在评估阶段我们不需要梯度。
还有一个类对于autograd实现非常重要那就是Function。Tensor和Function互相连接并构建一个非循环图，它保存整个完整的计算过程的历史信息。每个张量都有一个.grad_fn属性保存着创建了张量的Function的引用（如果用户自己创建张量，则grad_fn是None）。
如果你想计算导数，你可以调用Tensor.backward()。如果Tensor是标量（即它包含一个元素数据），则不需要指定任何参数backward()，但是如果它有更多元素，则需要指定一个gradient参数来指定张量的形状。

transforms方法

裁剪
a. transforms.CenterCrop
b. transforms.RandomCrop
c. transforms.RandomResizedCrop
d. transforms.FiveCrop
e. transforms.TenCrop

翻转和旋转
a. transforms.RandomHorizontalFlip
b. transforms.RandomVerticalFlip
c. transforms.RandomRotation

图像变换
a. transforms.Pad
b. transforms.ColorJitter
c. transforms.Grayscale
d. transforms.RandomGrayscale
e. transforms.RandomAffine
f. transforms.LinearTransformation
g. transforms.RandomErasing
h. transforms.Lambda
i. transforms.Resize
j. transforms.Totensor
k. transforms.Normalize

transforms的操作
a. transforms.RandomChoice
b. transforms.RandomApply
c. transforms.RandomOrder

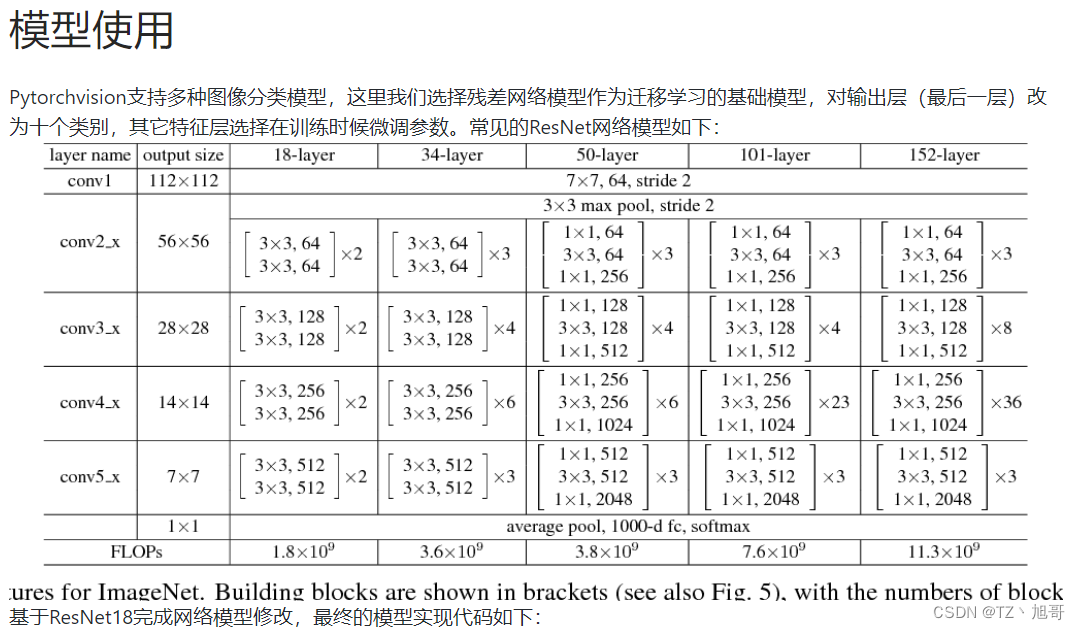
迁移学习

迁移学习就是利用数据、任务或模型之间的相似性，将在旧的领域学习过或训练好的模型，应用于新的领域这样的一个过程。从这段定义里面，我们可以窥见迁移学习的关键点所在，即新的任务与旧的任务在数据、任务和模型之间的相似性。
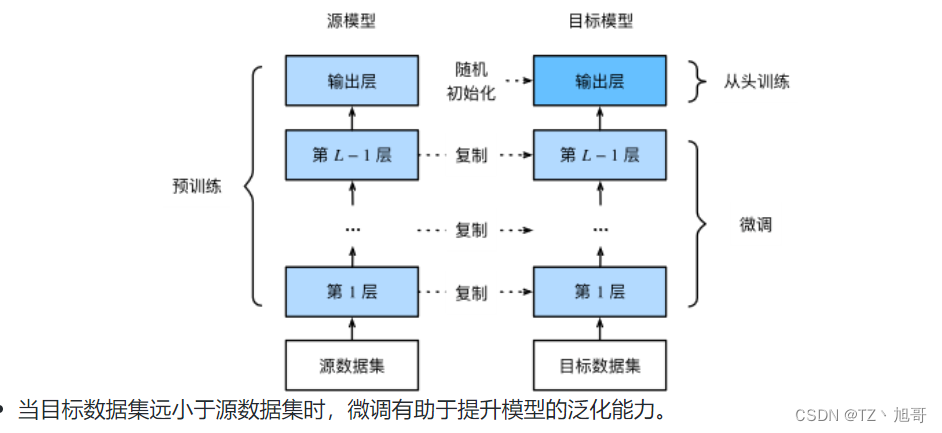
本节我们介绍迁移学习中的一种常用技术：微调（fine tuning）。微调由以下4步构成。
在源数据集（如ImageNet数据集）上预训练一个神经网络模型，即源模型。
创建一个新的神经网络模型，即目标模型。它复制了源模型上除了输出层外的所有模型设计及其参数。我们假设这些模型参数包含了源数据集上学习到的知识，且这些知识同样适用于目标数据集。我们还假设源模型的输出层跟源数据集的标签紧密相关，因此在目标模型中不予采用。
为目标模型添加一个输出大小为目标数据集类别个数的输出层，并随机初始化该层的模型参数。
在目标数据集（如FashionMNIST数据集）上训练目标模型。我们将从头训练输出层，而其余层的参数都是基于源模型的参数微调得到的。

在这里插入图片描述

class SurfaceDefectResNet(torch.nn.Module):
    def __init__(self):
        super(SurfaceDefectResNet, self).__init__()
        # Downloading: "https://download.pytorch.org/models/resnet18-5c106cde.pth" to /home/admin/.cache/torch/hub/checkpoints/resnet18-5c106cde.pth
        # 加载模型 及其 所有参数
        self.cnn_layers = torchvision.models.resnet18(pretrained=True)	
        # 定义了一个变量 "num_ftrs"，表示模型中全连接层(fc)的输入特征数。
        num_ftrs = self.cnn_layers.fc.in_features
        # 修改了模型中的全连接层，将输入特征数设置为 "num_ftrs"，输出特征数设置为 10。
        self.cnn_layers.fc = torch.nn.Linear(num_ftrs, 10)

    def forward(self, x):
        # stack convolution layers
        out = self.cnn_layers(x)
        return out

net = SurfaceDefectResNet()