343. 整数拆分

Leetcode

思路

1. dp[i] 表示 分拆数字i，可以得到的最大乘积为dp[i]。
2. dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))

贪心解法

这里粘贴一下美版 StefanPochmann 老哥的 idea（一句话就直观理解数学方法）
You’re making it pretty complicated. If an optimal product contains a factor f >= 4, then you can replace it with factors 2 and f-2 without losing optimality, as 2*(f-2) = 2f-4 >= f. So you never need a factor greater than or equal to 4, meaning you only need factors 1, 2 and 3 (and 1 is of course wasteful and you’d only use it for n=2 and n=3, where it’s needed). For the rest I agree, 3*3 is simply better than 2*2*2, so you’d never use 2 more than twice.

总结就是有3就分解3，剩下4的时候不用分解。

代码

动态规划

class Solution:
         # 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：
        # 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
        # 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]
    def integerBreak(self, n):
        dp = [0] * (n + 1)   # 创建一个大小为n+1的数组来存储计算结果
        dp[2] = 1  # 初始化dp[2]为1，因为当n=2时，只有一个切割方式1+1=2，乘积为1
       
        # 从3开始计算，直到n
        for i in range(3, n + 1):
            # 遍历所有可能的切割点
            for j in range(1, i // 2 + 1):

                # 计算切割点j和剩余部分(i-j)的乘积，并与之前的结果进行比较取较大值
                
                dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)
        
        return dp[n]  # 返回最终的计算结果

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

96.不同的二叉搜索树

Leetcode

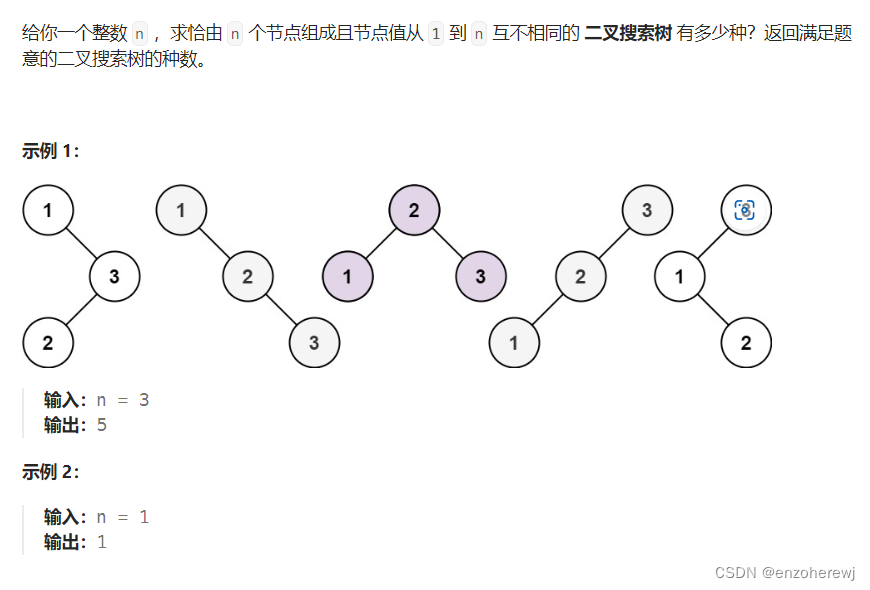
思路

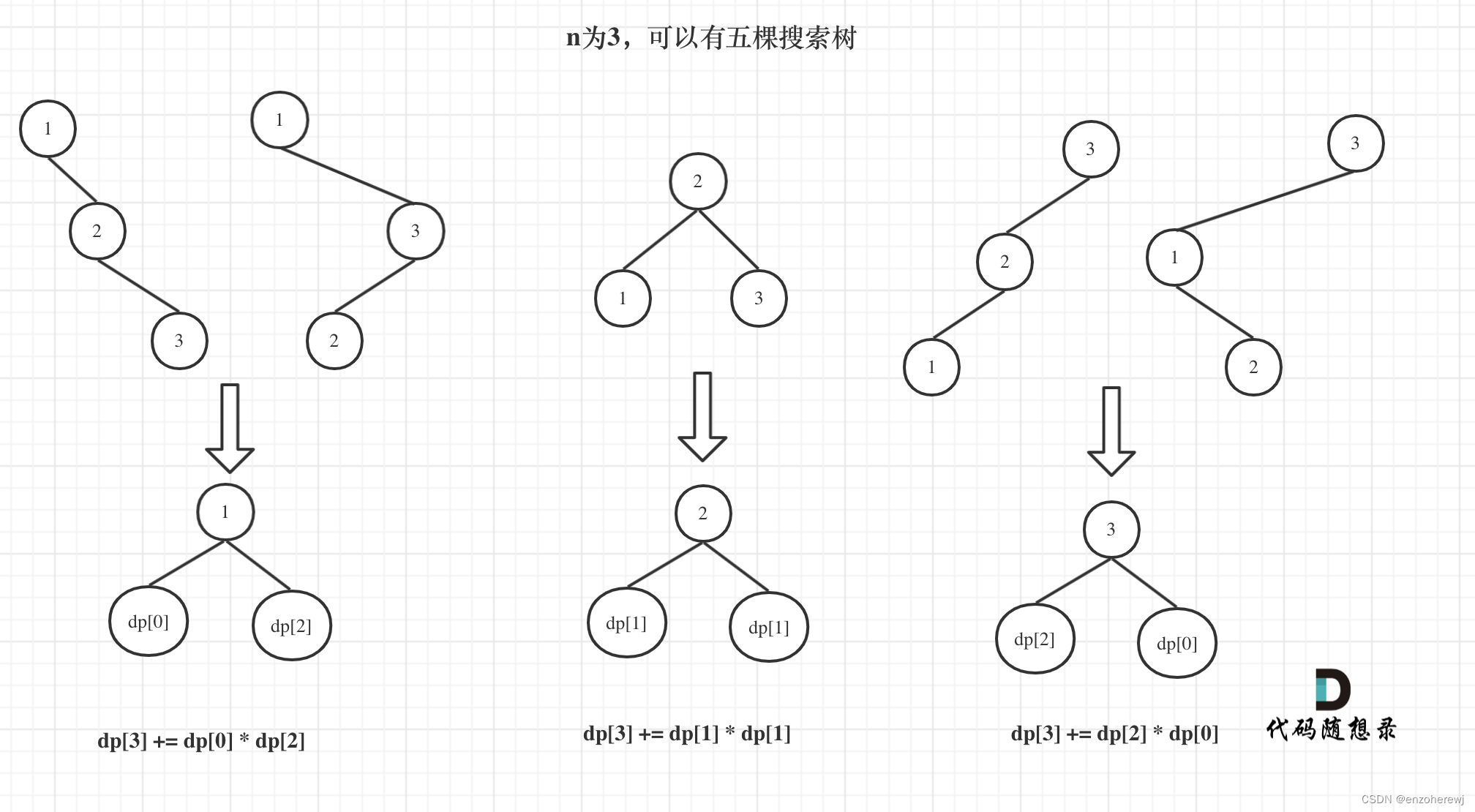
代码

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0] * (n + 1)  # 创建一个长度为n+1的数组，初始化为0
        dp[0] = 1  # 当n为0时，只有一种情况，即空树，所以dp[0] = 1
        for i in range(1, n + 1):  # 遍历从1到n的每个数字
            for j in range(1, i + 1):  # 对于每个数字i，计算以i为根节点的二叉搜索树的数量
                dp[i] += dp[j - 1] * dp[i - j]  # 利用动态规划的思想，累加左子树和右子树的组合数量
        return dp[n]  # 返回以1到n为节点的二叉搜索树的总数量

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$