期权定价模型系列第6篇文章

---

1. 前言

对于欧式期权，最常用的是BS模型，此外，也可也用蒙特卡洛模拟方法求解欧式期权的价格。当然，对于美式期权，也同样可以用蒙特卡洛模拟方法来求解，一般对美式更多用的是二叉树模型。

本篇内容将介绍如何用二叉树模型对美式期权与百慕大期权进行定价。无论是蒙特卡洛模拟还是二叉树方法，都是常见的数值模拟方法。这里进行简单的介绍。

2.蒙特卡洛模拟

蒙特卡洛模拟最重要的应用之一是对未定权益，如期权、衍生品、混合型工具的估值。在风险世界中，未定权益的价值是风险中立（鞅）测度下的折现后的预期收益。

蒙特卡洛模拟需要用到风险中立世界思想。其基本思路为：尽可能的模拟风险中性世界中标的资产价格的多种路径，计算每种路径下的期权回报均值，再贴现就可得期权价格。
①在风险中性世界里对S的随机路径进行抽样，这就给出了标的资产价格路径的一个实现。
②计算这条路径下的期权回报。
③重复计算步骤①、②，得到许多样本结果，即风险中性世界中的期权回报值。
④计算这些回报的均值，得到风险中性世界中的预期期权回报值。
⑤用无风险利率进行贴现，得到这个期权的估计价值。
 

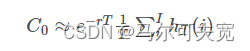
具体的代码可以参考之前的文章：

http://t.csdn.cn/Axhpdhttp://t.csdn.cn/Axhpd

3.二叉树方法

作为常用的数值方法，二项式期权定价模型（又称二叉树期权定价模型）是由Cox等人在1979年提出的。这种方法理解起来比较简单，而且数值实现过程可读性很高。

二项式模型的核心思想就是把持续期内的期权分成很多个小的时间间隔，并且假设在每一个时间间隔内标的资产价格只有上涨和下跌两种可能，上涨的概率为p，下跌的概率为1-p。

二叉树定价的逻辑非常简单，该模型假设标的资产价格在经过大量二元运动（上涨或下跌）之后达到目标价格，且每一步的上涨概率和下跌概率保持恒定，再通过不同概率下期末期权价格折现到现值以求得期权价格。

具体的计算原理和代码可以参考之前的文章：

http://t.csdn.cn/kSuDKhttp://t.csdn.cn/kSuDKhttp://t.csdn.cn/xFOU1http://t.csdn.cn/xFOU1

4.百慕大期权

百慕大期权(Bermudan option)一种可以在到期日前所规定的一系列时间行权的期权。 比如，期权可以有3年的到期时间，但只有在3年中每一年的最后一个月才能被执行，它的应用常常与固定收益市场有关。一般而言，百慕大期权的价格会高于欧式期权的价格，低于美式期权的价格。因此，对百慕大期权，可以采用欧式期权与美式期权常见的蒙特卡洛模拟方法与二叉树方法进行求解。大概思路可以是在欧式范围内采用欧式定价的算法，在美式范围内采用美式定价的算法。

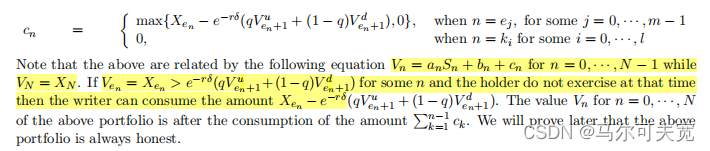
5.定价对比

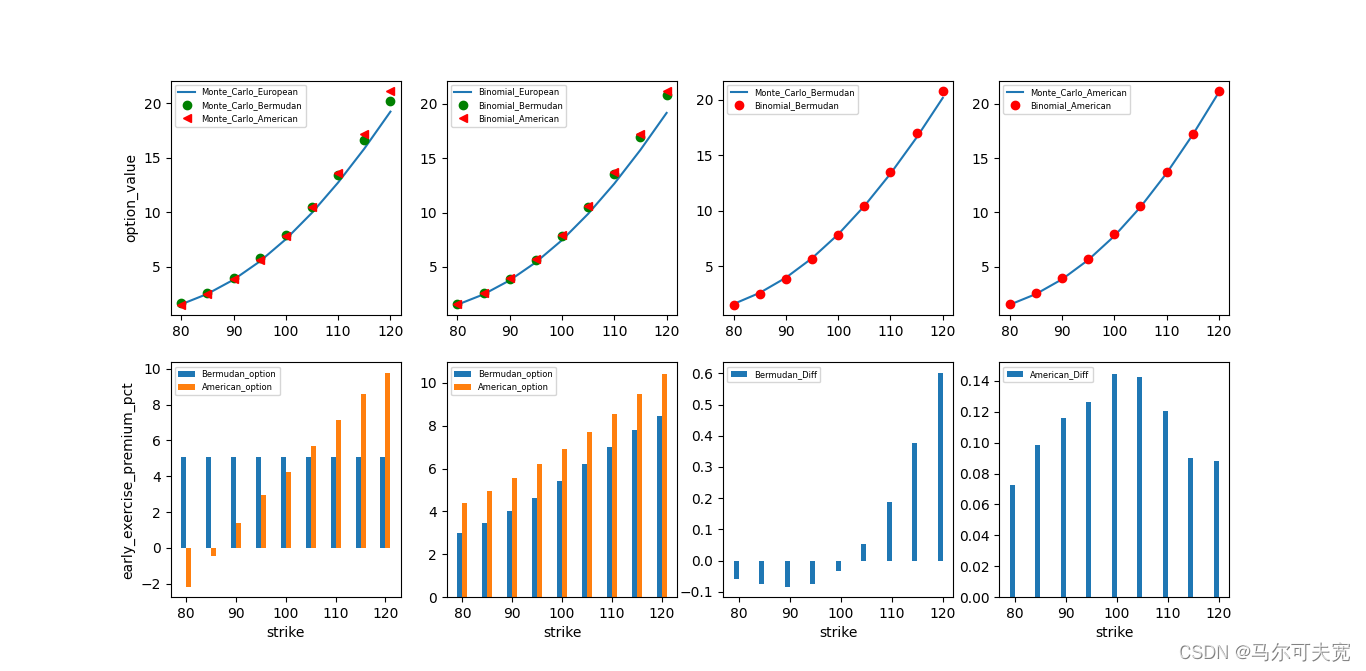
采用蒙特卡洛模拟方法与二叉树方法对欧式期权、百慕大期权与美式期权进行对比，结构如图所示：

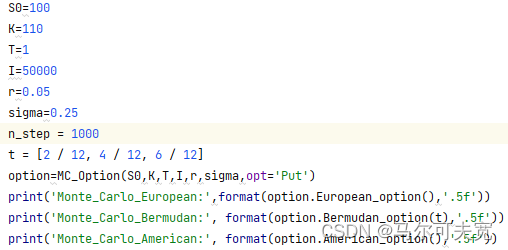
Monte_Carlo_European: 12.71083
Monte_Carlo_Bermudan: 13.35938
Monte_Carlo_American: 13.62204

Binomial_European: 12.65931
Binomial_Bermudan: 13.54806
Binomial_American: 13.74222