🌈write in front🌈
🧸大家好，我是Aileen🧸.希望你看完之后，能对你有所帮助，不足请指正！共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页：Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​
📣系列专栏：Aileen_0v0🧸的数据结构与算法学习系列专栏🌸——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马💫~"

目录

回顾💫

List 列表数据类型常用操作性能

Dict字典数据类型常用操作性能 

P、NP、NPC、NP-hard问题详解

1. 多项式时间（Polynomial time）

2. 确定性算法与非确定性算法

确定性算法：

非确定性算法：

3. 规约/约化

4. P类问题、NP类问题、NPC问题

P类问题:

NP类问题：

NPC问题(NP-complete):

NP难问题：

---

回顾💫

"温故而知新"~

上回儿说到,什么是时间复杂度,空间复杂度,

以及变位词问题的四种解法,以及内置函数sorted和sort.()的内置函数拓展

不记得的朋友可以点击🔗http://t.csdn.cn/04nTx进行快速定位,接下来进行new knowledge 的学习

​

后面我们会用来实现各种数据结构

通过运行试验来估计其各种操作运行时间数量级

​

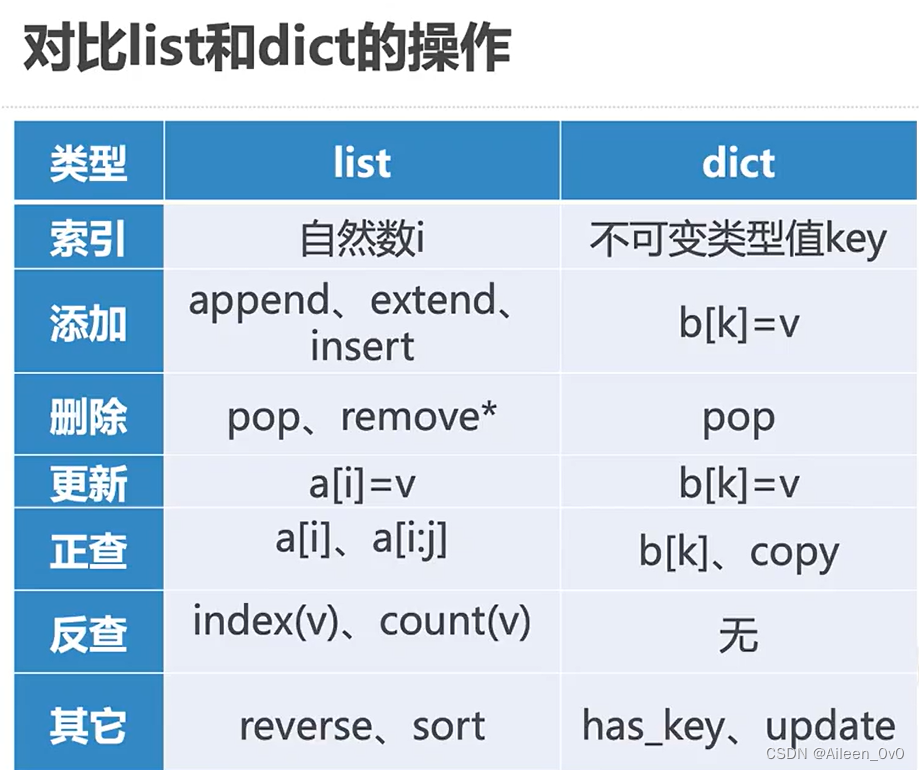
List 列表数据类型常用操作性能🍒

最常用的:按索引取值和赋值( v = a [i]-->取值操作, a [i] = v-->赋值操作)

由于 列表随机访问特性 , 这两个操作执行时间与列表大小无关 , 均为O(1)

另一个是列表增长, 可以选择append() 和  _add_() " + "

lst.append(v), 执行时间 O(1)

lst = lst + [V],列表中加一个列表, 执行时间是O(n+k),其中 k 是被加的列表长度

选择哪个方法来操作列表,决定了程序的性能

4种生成前n个整数列表的方法:

#首先是循环连接列表( + ) 方式生成
def test1():
    l = []
    for i in range(1000):
        l = l + [i]

#然后用append方法添加元素生成
def test2():
    l = []
    for i in range(1000):
        l.append(i)

#用列表推导式来生成
def test3():
    l = [i for i  in range(1000)]

#最后 利用 range函数 调用转成 列表
def test4():
    l = list(range(1000))

​

Dict字典数据类型常用操作性能🍌 

​

P、NP、NPC、NP-hard问题详解🫐

 想要理解P问题、NP问题、NPC问题、NP-hard问题，需要先弄懂几个概念：

什么是多项式时间(inpolynomial多项式  time)？
什么是确定性算法？什么是非确定性算法？
什么是规约/约化？

1. 多项式时间（Polynomial time）🍈

时间复杂度是衡量算法执行效率的一个指标，它表示算法运行时间与问题规模之间的增长关系。通常用大O符号来表示。

常见的时间复杂度类型有：

1. 常数阶 O(1)
2. 对数阶 O(log n)
3. 线性阶 O(n)
4. 线性对数阶 O(n log n)
5. 平方阶 O(n^2)
6. 立方阶 O(n^3)
7. 指数阶 O(2^n)
8. 阶乘阶 O(n!)

1. 常数时间复杂度 O(1)：无论输入的数据规模如何变化，算法的执行时间都是恒定的                        示例：访问数组中固定下标的元素，或者执行单次的加减乘除运算等。
2. 对数时间复杂度 O(log n)：当输入规模增加时，算法执行时间相对于输入规模增加的比率不大。                                                                                                                                                    示例：二分查找算法。
3. 线性时间复杂度 O(n)：算法执行时间与输入规模是正比的。                                                            示例：遍历一次长度为 n 的数组，或者进行一次循环 从1到n 累加求和等。
4. 平方时间复杂度 O(n^2)：算法执行时间与输入规模平方成正比。                                                    示例：双重循环嵌套的算法，比如冒泡排序、插入排序等。
5. 指数时间复杂度 O(2^n)：算法执行时间的增长率与输入规模的指数成正比。                                  示例：穷举算法，比如求解最长公共子序列问题的暴力算法。

还有其他更高阶的时间复杂度，比如阶乘时间复杂度 O(n!)，递归时间复杂度 O(2^n) 等，但是这些复杂度通常不会出现在实际应用中，因为它们的执行时间会随着输入规模的增加而急剧增长，算法的效率非常低下。

像 O(1),O(ln(n)),O(n^a) 等，我们把它叫做多项式级复杂度，因为它的规模n出现在底数的位置；另一种像是 O(a^n) 和 O(n!) 等，它是非多项式级的复杂度，其复杂度计算机往往不能承受。当我们在解决一个问题时，我们选择的算法通常都需要是多项式级的复杂度，非多项式级的复杂度需要的时间太多，往往会超时，除非是数据规模非常小。

2. 确定性算法与非确定性算法🍑

确定性算法：

设A是求解问题B的一个解决算法，在算法的整个执行过程中，每一步都能得到一个确定的解，这样的算法就是确定性算法。

非确定性算法：

设A是求解问题B的一个解决算法，它将问题分解成两部分，分别为猜测阶段和验证阶段，其中

1. 猜测阶段：在这个阶段，对问题的一个特定的输入实例x产生一个任意字符串y，在算法的每一次运行时，y的值可能不同，因此，猜测以一种非确定的形式工作。
2. 验证阶段：在这个阶段，用一个确定性算法（有限时间内）验证。                                       ①检查在猜测阶段产生的y是否是合适的形式，如果不是，则算法停下来并得到no；           ② 如果y是合适的形式，则验证它是否是问题的解，如果是，则算法停下来并得到yes，否则算法停下来并得到no。它是验证所猜测的解的正确性。

3. 规约/约化🍊

问题A可以约化为问题B，称为“问题A可规约为问题B”，可以理解为问题B的解一定就是问题A的解，因此解决A不会难于解决B。由此可知问题B的时间复杂度一定大于等于问题A。

 规约就是选择一个文法规则：X→ABC,依次从栈顶弹出C、B、A，再将X压进栈。规范规约是文法中句子的一个最右推导的逆过程，而最左推导对应的是最右规约 。

再例如《算法导论》中有一个例子：现在有两个问题：求解一个一元一次方程和求解一个一元二次方程。那么我们说，前者可以规约为后者，意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题，那么我们能找到一个“规则”，按照这个规则把解一元一次方程程序的输入数据变一下，用在解一元二次方程的程序上，两个程序总能得到一样的结果。这个规则即是：两个方程的对应项系数不变，一元二次方程的二次项系数为0。

从规约的定义中我们看到，一个问题规约为另一个问题，时间复杂度增加了，问题的应用范围也增大了。通过对某些问题的不断规约，我们能够不断寻找复杂度更高，但应用范围更广的算法来代替复杂度虽然低，但只能用于很小的一类问题的算法。存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。这种问题的存在难以置信，并且更加不可思议的是，这种问题不只一个，它有很多个，它是一类问题。这一类问题就是传说中的NPC问题，也就是NP-完全问题。

4. P类问题、NP类问题、NPC问题、NP难问题🍍

P类问题:

It is the set of problems which can be solved by some algorithms inpolynomial time.  --->能在多项式时间内可解的问题.

故事案例🌰:

柯尼斯堡七桥问题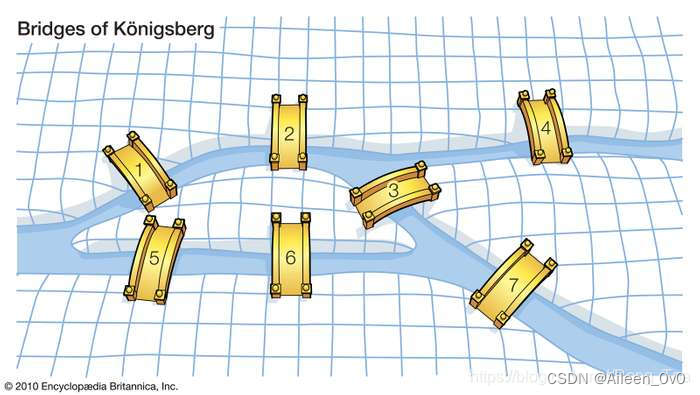

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如右上图）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。后来大数学家欧拉把它转化成一个几何问题（如左图下）——一笔画问题。他不仅解决了此问题，且给出了连通图可以一笔画的充要条件是：

⒈任意点连接的边数为偶数

⒉拥有奇数边点的个数为2或0.

⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。)

一起来玩游戏吧~

判断下图能否一笔画:

 

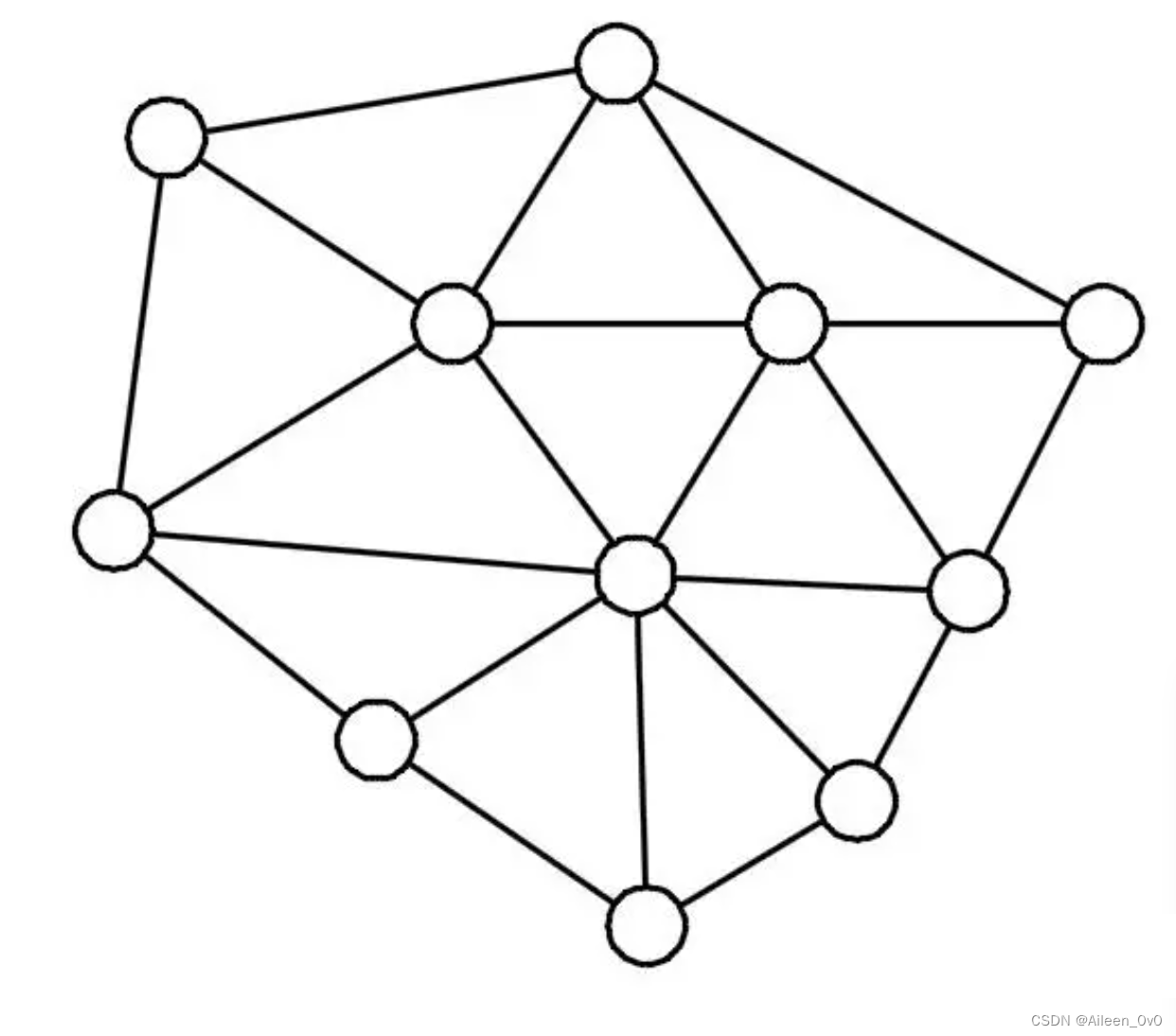
答案是没有解，因为只有当拥有奇数条边的顶点数量小于或者等于2个时才会有解，而图中有8个粉红色顶点有奇数条边，所以无解。

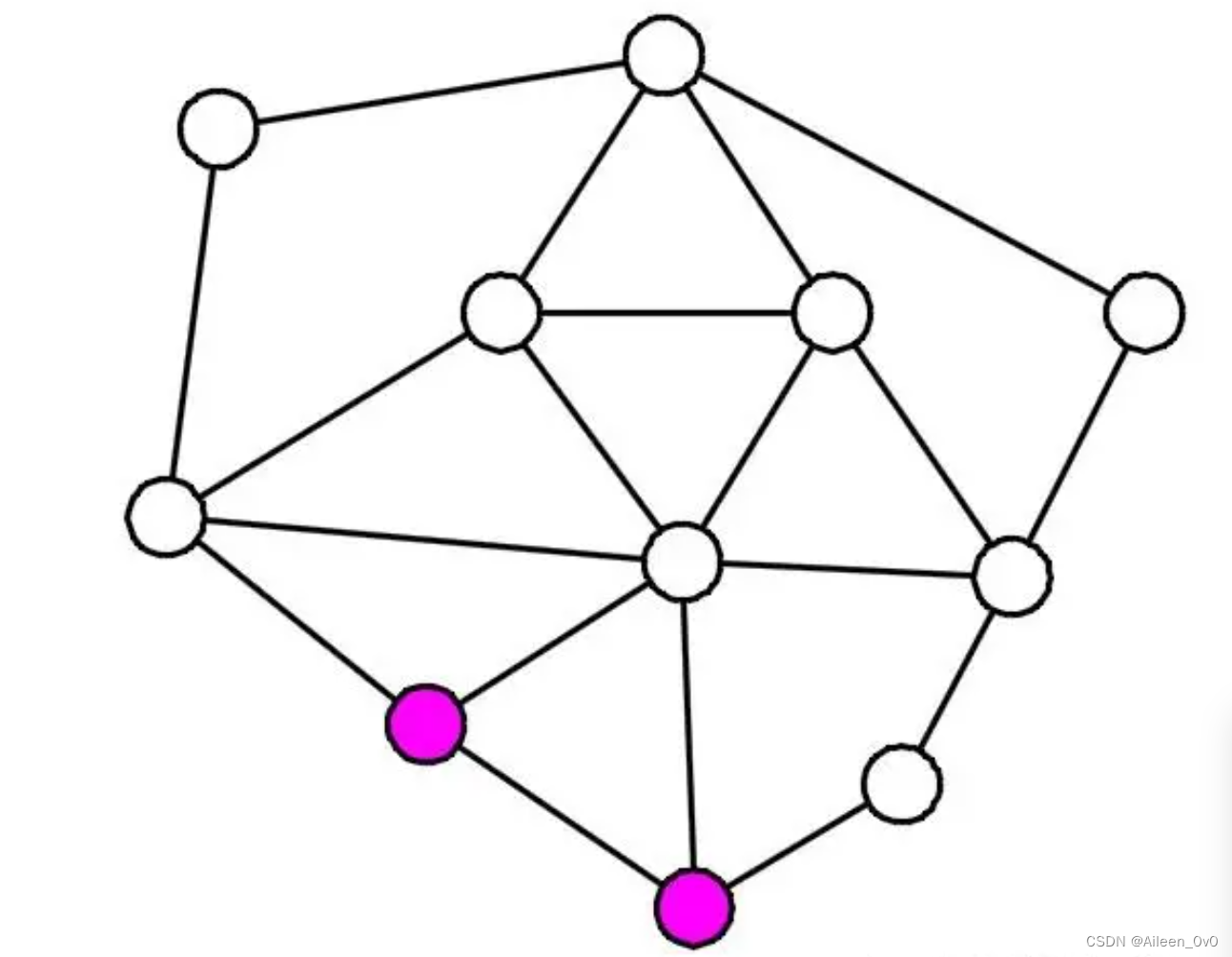
有解 

NP类问题：

lt is the set of problems which are not sure whether it can be solved bysome algorithms in polynomial time. But it is possible to verify the answer in polynomial time.  --->不确定可以在多项式时间内解决的问题.在多项式时间内“可验证”的问题。也就是说，不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的猜测过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。P类问题属于NP问题，但NP类问题不一定属于P类问题。

故事案例🌰:

1859 年，爱尔兰数学家哈密尔顿（Hamilton）提出了一个“周游世界”的游戏

下图中(a)，哈密顿提出的「周游世界」的游戏。把一个正十二面体的二十个顶点看成地球上的二十个城市。要求游戏者沿棱线走，寻找一条经过所有结点一次且仅一次的回路，(b)是其哈密顿图，哈密顿回路由实线标出。

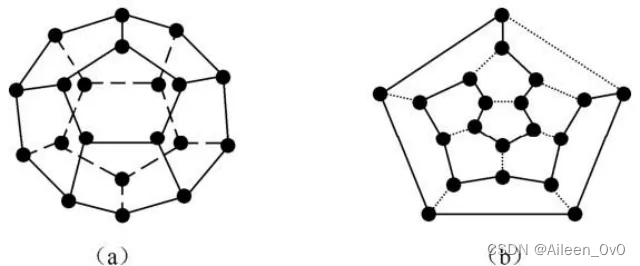
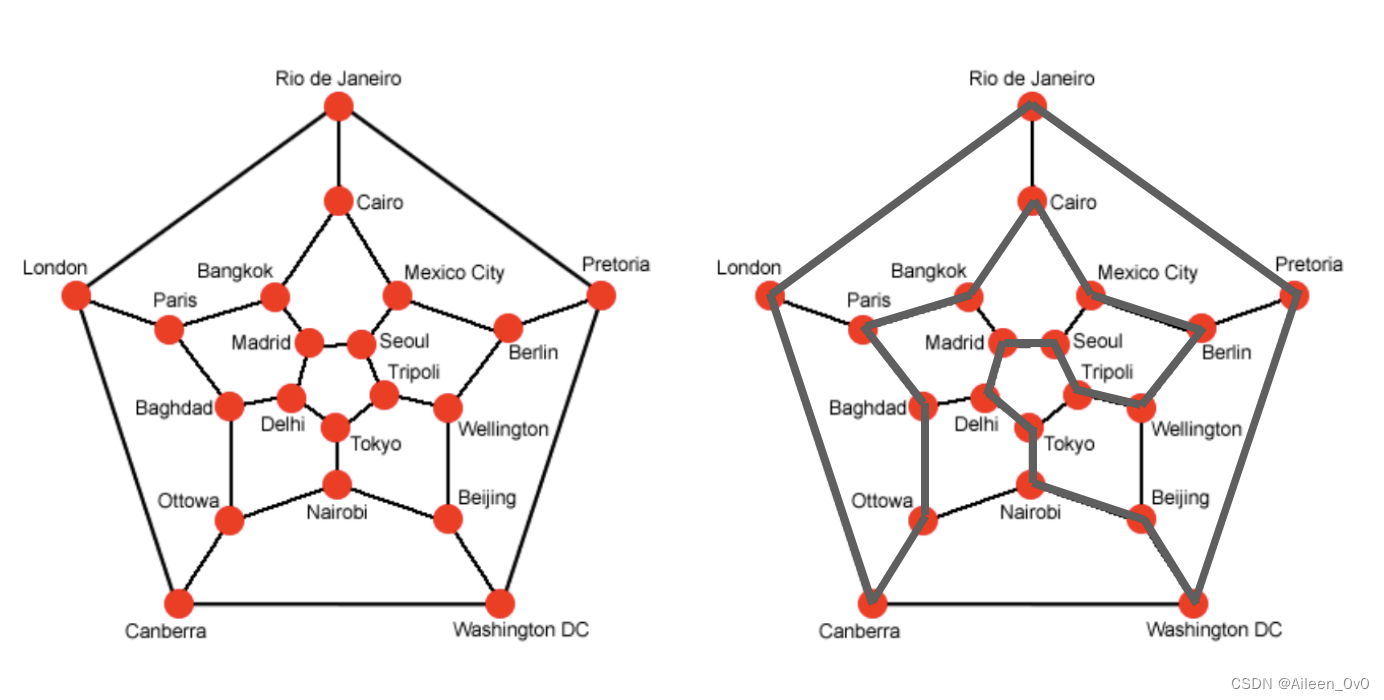
简而言之，哈密尔顿回路是指，从图中的一个顶点出发，沿着边行走，经过图的每个顶点，且每个顶点仅访问一次，之后再回到起始点的一条路径。如上图所示，我们的起始点选定为 Washington DC，灰色实线构成的一条路径就是一条哈密尔顿回路。

在图论算法的领域中，哈密尔顿回路(Hamilton Loop)和路径(Hamilton Path)在定义上是有所区分的：

哈密尔顿回路(Hamilton Loop)要求从起始点出发并能回到起始点，其路径是一个环。

哈密尔顿路径(Hamilton Path)并不要求从起始点出发能够回到起始点，也就是说：起始顶点和终止顶点之间不要求有一条边。

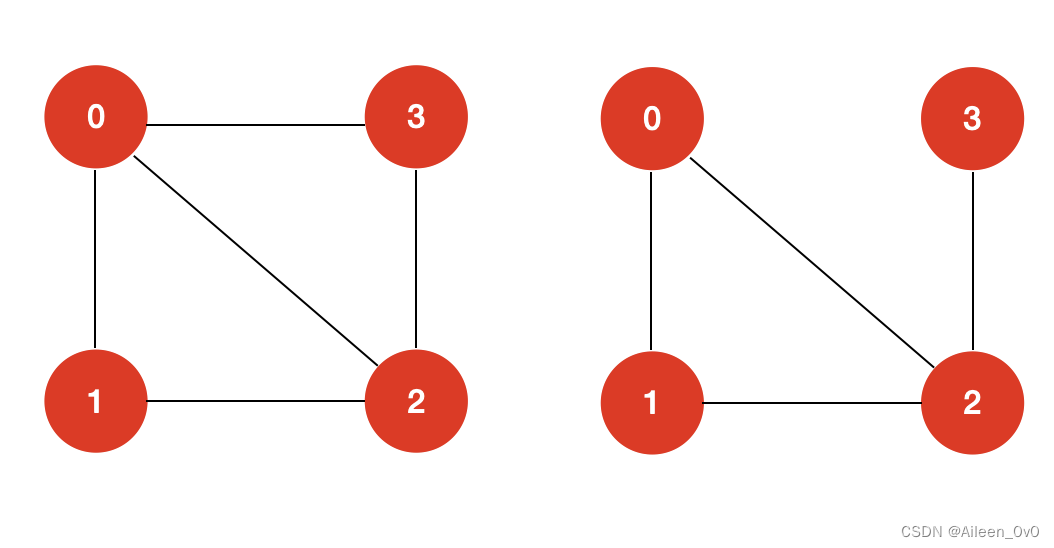
比如上面这两个图，左图既存在哈密尔顿回路，也存在哈密尔顿路径。而右图只存在哈密尔顿路径，并不存在哈密尔顿回路。 

如何求解一个图是否存在哈密尔顿回路呢？

一个最直观的想法就是暴力求解。暴力求解的思路也很简单：我们遍历图的每一个顶点 v，然后从顶点 v 出发，看是否能够找到一条哈密尔顿回路。

暴力求解和求解全排列问题是等价的，其时间复杂度为 O ( N ! ) ,N 为图的顶点的个数。

O ( N ! ) 是一个非常高的复杂度，它并不是一个多项式级别的复杂度。像 O ( 1 ) , O(NlogN)，O(N^2)这些我们常见的复杂度都是多项式级的复杂度，而O(a^N),O ( N ! )这些复杂度是非多项式级的，也就是说，在数据量 N 极大的情况下，我们的现代计算机是不能承受的。

那么除了暴力求解哈密尔顿回路问题，是否存在更好的算法？

很遗憾的是，对于哈密尔顿问题，目前并没有多项式级别的算法。我们只能在暴力破解的基础上，尽量去做到更多的优化，譬如回溯剪枝，记忆化搜索等，但是，还没有找到一种多项式级别的算法来解决哈密尔顿问题。

通常，这类问题也被称为 NP(Non-deterministic Polynomial)难问题。

NPC问题(NP-complete):

they are the problems which are the hardest in NP. If they can be solved in polynomial time, all NP problem can be solved inpolynomial time.存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件：

1. 它是一个NP问题；
2. 所有NP问题都能规约到它。

故事案例🌰:

设有p个城镇，已知每两个城镇之间的距离，一个售货员从某一城镇出发巡回售货，问这个售货员应如何选择路线，能使每个城镇经过一次且仅一次，最后返回到出发地，而使总的行程最短？这个问题称为旅行售货员问题。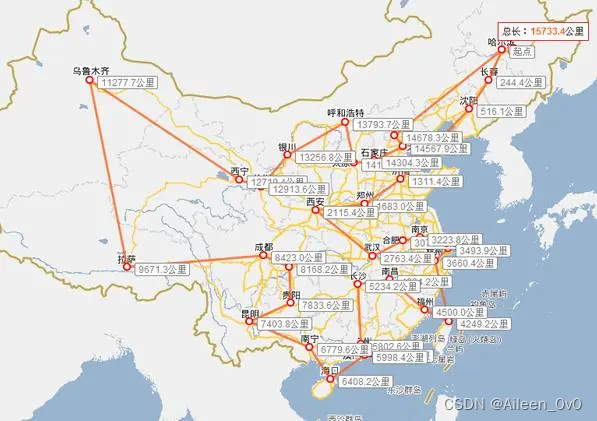 

NP难问题：

NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 NPC问题的范围广，NP-Hard问题没有限定属于NP），即所有的NP问题都能约化到它，但是他不一定是一个NP问题。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决

上面四个问题的关系图: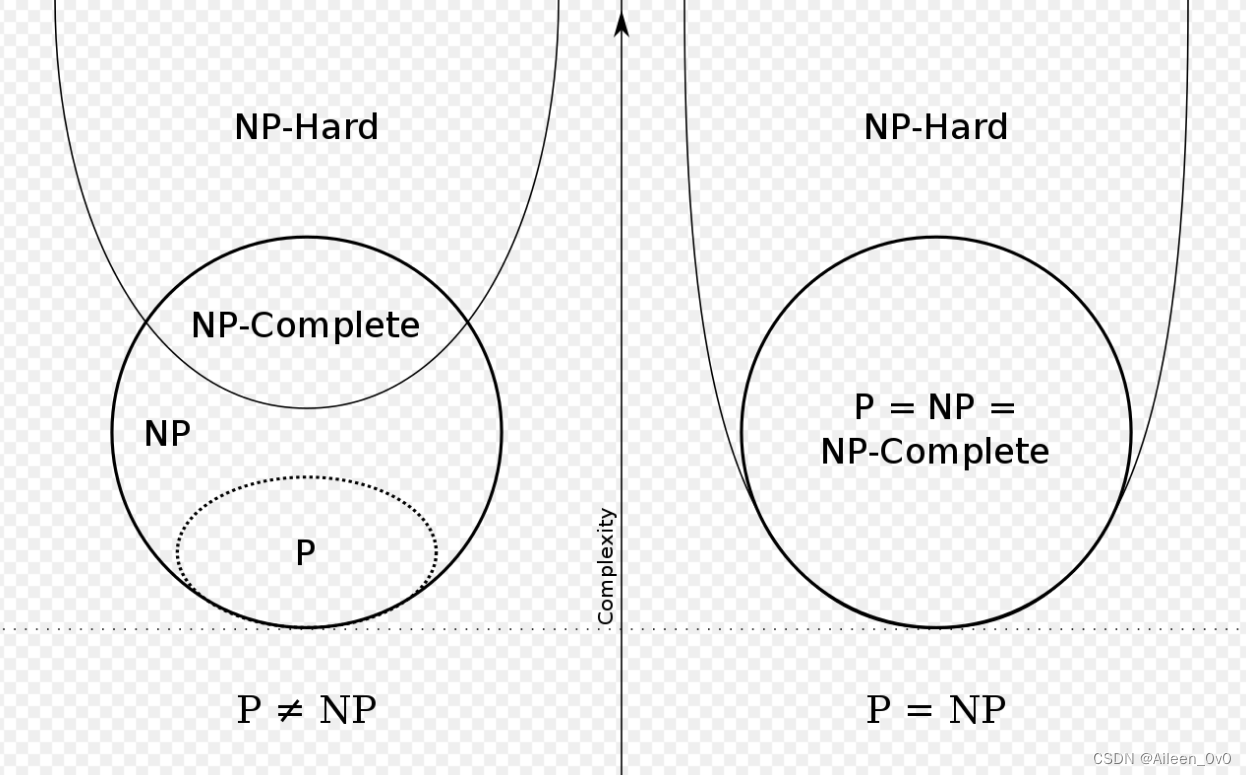 

🐻今天的内容就分享到这里啦~🐻

🐻喜欢就三连一下呗~🐻

🐻感谢支持💖!🐻