概念

分治法（Divide and Conquer）是一种算法设计策略，其思想是将一个大问题划分为若干小规模的子问题，然后递归地解决每个子问题，并将它们的解合并起来以得到原始问题的解。分治法包含三个基本步骤：分解、解决和合并。

分解（Divide）：将原始问题划分为若干个规模较小且相互独立的子问题。这个步骤通常通过递归地将问题分解为更小的子问题来实现。分解的过程要求每个子问题的规模都比原始问题的规模小，且子问题之间没有重叠。

解决（Conquer）：递归地解决每个子问题。当子问题足够小，可以直接求解时，可以采用基本的求解方法或直接返回已知的解。

合并（Combine）：将子问题的解合并起来，得到原始问题的解。这个步骤通常是将各个子问题的解组合成原问题的解。在合并的过程中，可能需要进行一些额外的计算或操作。

分治法的核心思想是将复杂的问题分解为一系列相对简单的子问题，然后通过递归地求解子问题，最终将子问题的解合并起来得到原始问题的解。该算法设计策略通常用于解决一些具有重复性结构的问题，如排序、查找、图搜索等。通过将大问题划分为小问题，并使用递归思想求解，可以降低问题的复杂度，提高算法的效率。

值得注意的是，分治法在应用时需要满足以下两个基本要求：子问题的规模较小且相互独立，以及问题的结构具有递归性质。只有满足这两个要求，分治法才能够发挥其优势并得到正确的解。

原理和步骤

当使用分治法解决问题时，我们遵循以下详细步骤：

分解（Divide）：将原始问题划分为若干个规模较小且相互独立的子问题。这个步骤的关键是找到一种方法将大问题划分为小问题，确保子问题的规模比原问题更小，并且子问题之间没有重叠。

解决（Conquer）：递归地求解每个子问题。每个子问题的解可以通过直接求解或进一步分解为更小的子问题来获得。如果子问题足够小，可以使用基本的解决方法或直接返回已知的解。

合并（Combine）：合并子问题的解来获得原始问题的解。在这个步骤中，我们将子问题的解合并起来，通常需要进行一些额外的计算或操作。

下面我们以计算数组中元素和的问题为例来详细说明分治法的原理。

假设我们有一个数组，我们想要计算数组中所有元素的和。

分解（Divide）：将数组划分为两个部分，每个部分包含大约一半的元素。例如，将数组从中间位置拆分成两个子数组。

解决（Conquer）：递归地对每个子数组进行求和。如果子数组足够小，我们可以直接对每个子数组进行求和并返回结果。

合并（Combine）：将子数组的和相加以获得原始数组的总和。在这个例子中，我们只需将两个子数组的和相加即可得到原始数组的总和。

通过以上步骤，我们就成功地使用分治法解决了计算数组元素和的问题。

需要注意的是，对于某些情况下，我们可能需要考虑优化合并操作的方法。例如，在归并排序算法中，我们可以使用合并操作的线性时间复杂度的方法来优化整体算法的效率。

分治法是一种将大问题划分为小问题、递归地求解子问题并合并子问题解的算法设计策略。它的基本步骤包括分解、解决和合并。分治法的核心思想在于将问题划分为规模更小且相互独立的子问题，并通过递归地求解每个子问题来最终解决原始问题。通过合理地应用分治法，我们可以提高算法的效率并解决各种复杂的问题。

代码示例

public class DivideAndConquer {
    public static int sum(int[] nums) {
        return sumHelper(nums, 0, nums.length - 1);
    }

    private static int sumHelper(int[] nums, int start, int end) {
        if (start == end) {  // 基本情况：只有一个元素
            return nums[start];
        } else {
            int mid = (start + end) / 2;  // 求中间位置
            int leftSum = sumHelper(nums, start, mid);  // 递归求左半部分的和
            int rightSum = sumHelper(nums, mid + 1, end);  // 递归求右半部分的和
            return leftSum + rightSum;  // 合并左右两部分的和
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5};
        int totalSum = sum(nums);
        System.out.println("数组的和为：" + totalSum);
    }
}

在上述代码中，sum 函数是调用方接口，用户只需传入整数数组，然后调用 sumHelper 函数进行辅助计算。sumHelper 函数是实际的递归函数，它根据传入的起始位置 start 和结束位置 end 来确定当前子问题的规模。

在 sumHelper 函数中，首先判断基本情况，即子数组只有一个元素时直接返回该元素的值。否则，通过求取中间位置 mid 将问题分解为两个较小的子问题，分别递归地计算左半部分和右半部分的和。最后，将左右两部分的和相加得到原始数组的总和。

在 main 函数中，我们创建一个示例数组 nums，然后调用 sum 函数计算数组的和，并打印结果。

运行该代码，输出结果为：数组的和为：15

总结

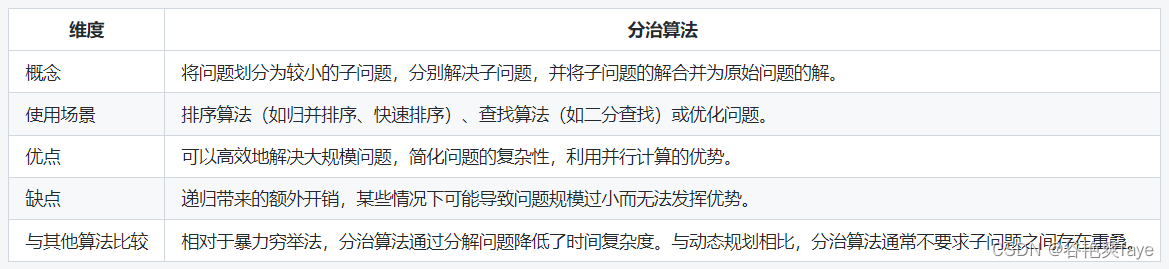
分治算法通过将问题划分为较小的子问题来解决复杂问题。它通常用于排序和查找问题，以及一些优化问题。分治算法的优点包括可以高效地解决大规模问题，简化问题的复杂性，并利用并行计算的优势。然而，分治算法的缺点在于递归过程中可能带来额外的开销，并且在某些情况下问题规模过小无法发挥优势。与暴力穷举法相比，分治算法通过分解问题降低了时间复杂度。与动态规划相比，分治算法通常不要求子问题之间存在重叠。

请注意，这只是一个简单的表格分析，实际上，随着问题的不同，分治算法的使用场景、优缺点等方面可能会有所变化。因此，在实际应用中，需要根据具体情况进行进一步评估和分析。