01背包问题 二维

背包问题汇总：

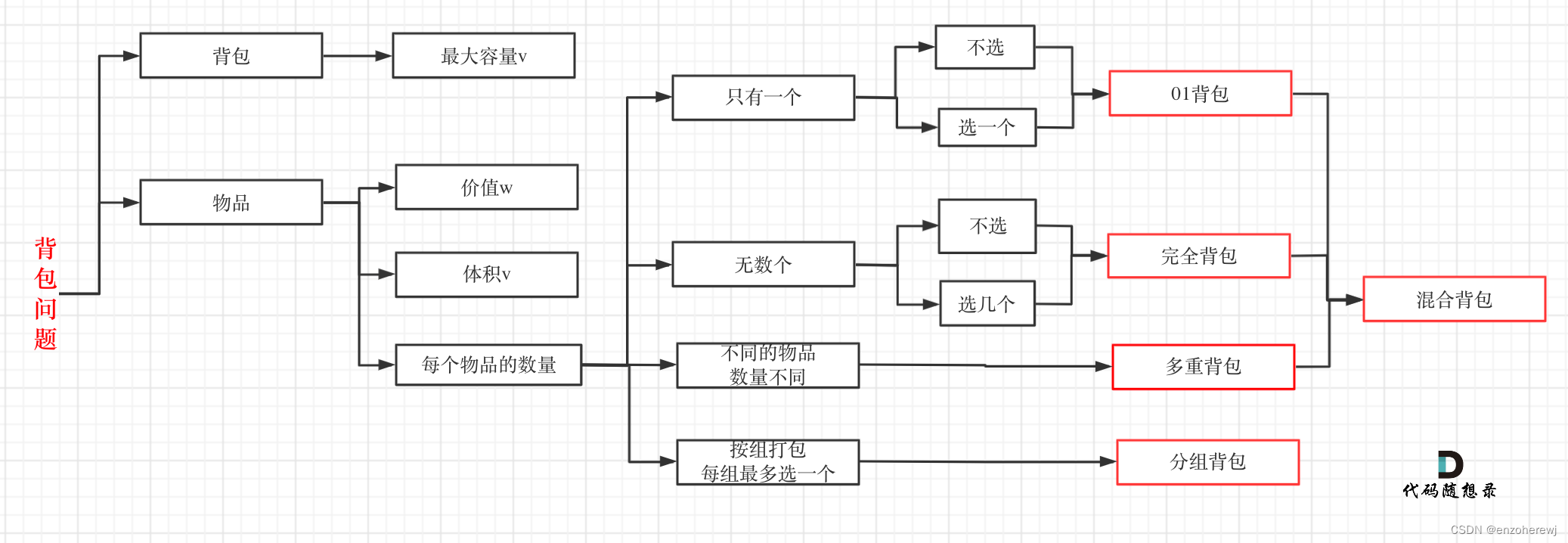
二维数组dp——01背包五部曲

1. dp[i][j]表示从下标为[0-i]的物品里面任意取，放进容量为j的背包，价值的总和最大是多少。
   

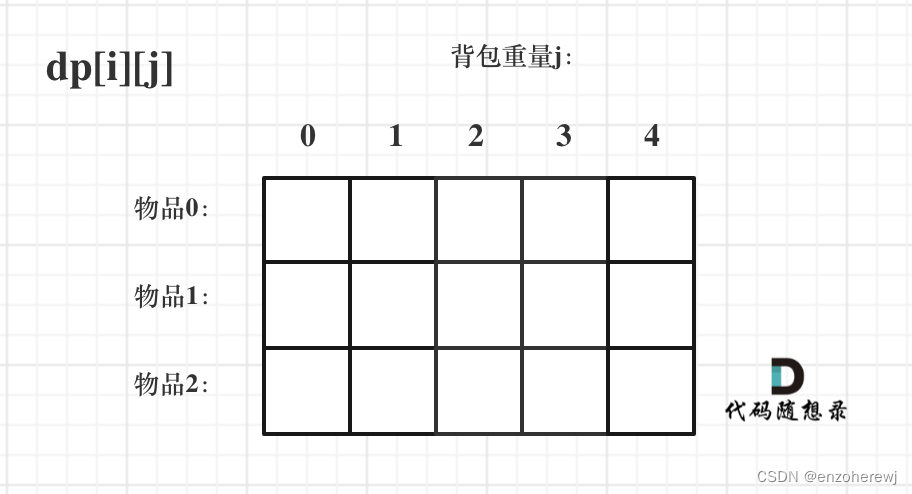
2. 递推公式：可以由两个方向推出dp[i][j]

   • 不放物品i：由dp[i - 1][j]推出
   • 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]]即为背包容量为j - weight[i]的时候不放物品i的最大价值。
     所以，dp[i - 1][j - weight[i]] + value[i]即为背包放入物品i后的最大价值。

   综上，对于来自两个方向的结果，我们取最大值即为dp[i][j]的最大值。所以，递推转换方程为，dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

3. 初始化：根据递推公式，求dp[i][j]时我们需要确保它的左上角已经有值了。
   所以初始化代码如下：

   for (int j = 0 ; j < weight[0]; j++) {  // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
       dp[0][j] = 0;
   }
   // 正序遍历
   for (int j = weight[0]; j <= bagweight; j++) {
       dp[0][j] = value[0];
   }
   

   所以初始化的情况如下图：

   
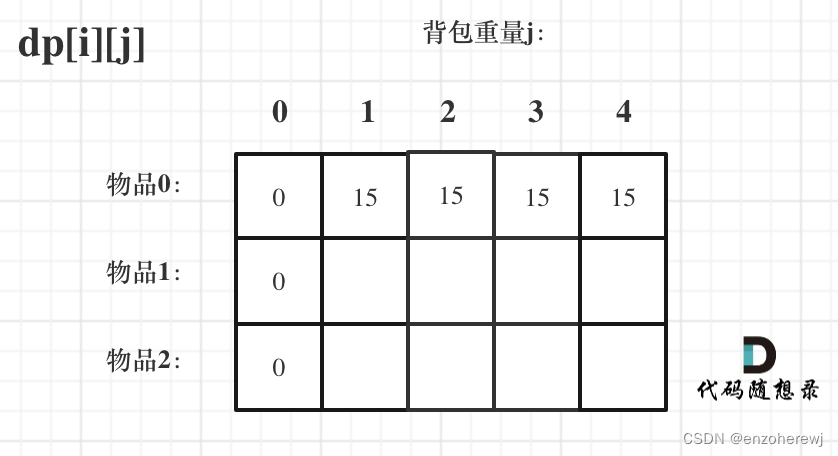
   其他的空格初始化的值可以是任意。

4. 遍历顺序：
   关于两个for loop先loop哪个，先遍历背包还是先遍历物品。其实都可以，因为他们都满足dp[i][j]的递推公式。如下图：
   先遍历物品，再遍历背包：
   
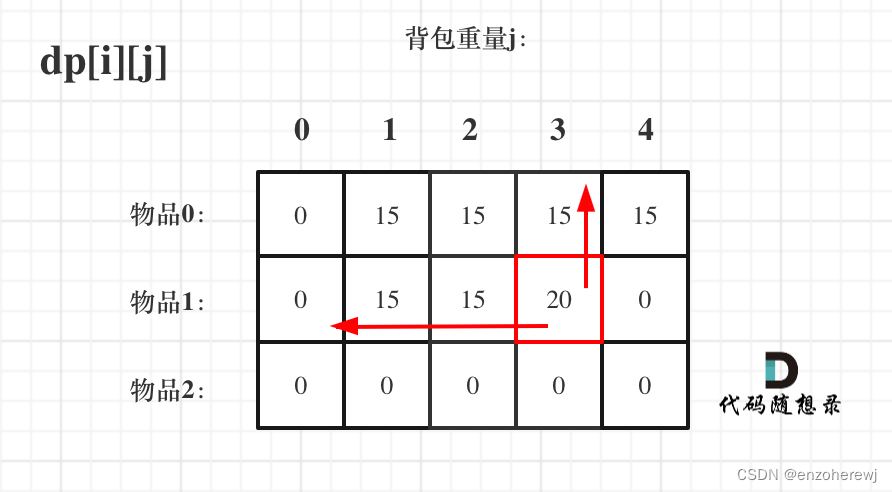
   先遍历背包，再遍历物品：
   
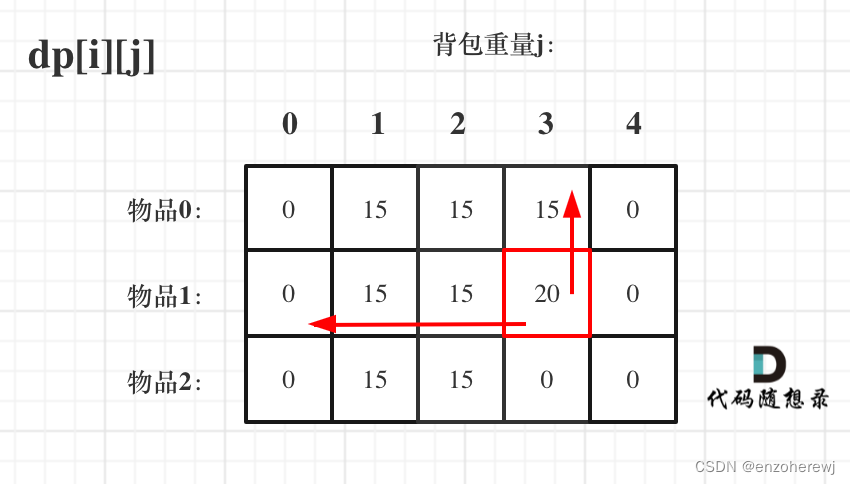
   实际上，如果想要倒序遍历也是可行的（详细参考一维滚动数组）。

代码

def backpack01_2d(weight, value, capacity):
    n = len(weight)
    dp = [[0 for _ in range(capacity+1)] for _ in range(n)]
    # initialize the dp table
    for j in range(weight[0], capacity+1):
        dp[0][j] = value[0]
    
    for i in range(1, n):
        for j in range(1, capacity + 1):
            if j >= weight[i]:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
            else:
                dp[i][j] = dp[i - 1][j]
    print(dp)
    return dp[-1][-1]

# generate some example to run the defined function
weight = [1, 3, 4]
value = [15, 20, 30]
capacity = 4
print(backpack01_2d(weight, value, capacity))

01背包问题（一维滚动数组）

一维数组和二维数组的区别在于：一维的滚动数组其实是压缩的二维数组。

五部曲：

1. dp[j]为容量为j的背包，所背的物品价值可以最大为dp[j]。
2. 递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
3. 初始化：dp[0] = 0，都初始为零
4. 遍历顺序：先遍历物品，再遍历背包，遍历背包需要倒序遍历，这样才能保证物品i只被放入一次。
   能够将遍历物品和遍历背包的顺序颠倒吗?
   因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

代码

def test_1_wei_bag_problem(weight, value, bagWeight):
    # 初始化
    dp = [0] * (bagWeight + 1)
    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    return dp[bagWeight]

weight = [1, 3, 4]
value = [15, 20, 30]
bagweight = 4
print(test_1_wei_bag_problem(weight, value, bagweight))

416. 分割等和子集

Leetcode

思路

二维数组：

1. dp[i][j]为在0-i之间的数字选择，能否相加之和为j
2. 递推公式：dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]] 可以选择或者不选择nums[i]这个数字
3. 初始化都为False, 然后dp[0][nums[0]] = True
4. 遍历顺序和01背包一样

一位滚动数组：
对于滚动数组，我们将其理解成01背包的形式。每个数字的重量和价值都等于数字。比如说5的重量和价值都是5。

1. dp[j]表示背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。
2. dp[j] = max(dp[j], dp[j - num] + num)，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

代码

二维数组

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        _sum = sum(nums)
        if _sum % 2 != 0:
            return False
        
        total = _sum // 2
        # 初始化 * 10001 是根据题目而定的最大可能距离
        # 为了避免像 [100] 这种edge case
        dp = [[False] * (10001) for _ in range(len(nums))]


        dp[0][nums[0]] = True

        for i in range(1, len(nums)):
            for j in range(1, total + 1):
                if j >= nums[i]:
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]]
                else:
                    dp[i][j] = dp[i - 1][j]

        return dp[-1][total]

• 时间复杂度: O(n^2)
• 空间复杂度: O(n^2)

一维滚动数组

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        _sum = sum(nums)
        if _sum % 2 != 0:
            return False
        
        total = _sum // 2
        dp = [0] * (total + 1)
        for num in nums:
            for j in range(total, num - 1, -1):
                dp[j] = max(dp[j], dp[j - num] + num)

        return dp[-1] == total

• 时间复杂度: O(n^2)
• 空间复杂度: O(n)