参考文献：

1. [CS05] Choi Y, Swartzlander E E. Parallel prefix adder design with matrix representation[C]//17th IEEE Symposium on Computer Arithmetic (ARITH’05). IEEE, 2005: 90-98.
2. [SV11] Smart N P, Vercauteren F. Fully homomorphic SIMD operations[J]. Designs, codes and cryptography, 2014, 71: 57-81.
3. [GHS12] Gentry C, Halevi S, Smart N P. Fully homomorphic encryption with polylog overhead[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 465-482.
4. [GHS12] Gentry C, Halevi S, Smart N P. Homomorphic evaluation of the AES circuit[C]//Annual Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 850-867.
5. [HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15): 8-36.
6. [ZQH+20] Zhang N, Qin Q, Hou Z, et al. Efficient comparison and addition for FHE with weighted computational complexity model[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020, 40(9): 1896-1908.

Carry-Lookahead Adder

给定两个整数 $A=a_{n-1}\cdots a_1{a}_0$，$B=b_{n-1}\cdots b_1{b}_0$，为了计算它们的加和，有多种加法器可以选择。我们使用以下逻辑符号：与门 $\cdot$，或门 $+$，异或门 $\oplus$，其中 $\cdot$ 的优先级最高。

全加器（Full Adder, FA）的输入 a , b , c i n ∈ { 0 , 1 } a,b,cin \in \{0,1\} a,b,cin∈{0,1}，输出 s o u t , c o u t ∈ { 0 , 1 } sout,cout \in \{0,1\} sout,cout∈{0,1}，逻辑表达式为：
$$\begin{array}{rl}sout& =a\oplus b\oplus cin\\ cout& =a\cdot b+a\cdot cin+b\cdot cin\end{array}$$

定义信号 $g=a\cdot b$（generate），$k=a+b$（kill），$p=a\oplus b$（propagate），那么
$$\begin{array}{rl}sout& =p\oplus cin\\ cout& =g+k\cdot cin\end{array}$$

Ripple-Carry Adder

行波进位加法器 （RCA）：将 $n$ 个全加器串联起来，输入 $A,B,c_0$，迭代计算，
$$\begin{array}{rl}{g}_i& =a_i\cdot b_i\\ k_i& =a_i+b_i\\ p_i& =a_i\oplus b_i\\ & \\ s_i& =p_i\oplus c_i\\ c_{i+1}& =g_i+k_i\cdot c_i\end{array}$$

关键路径的长度就是进位链 $c_1,\cdots ,c_{n-1},c_n$ 的迭代轮数 $O(n)$

Carry-Lookahead Adder

超前进位加法器（CLA）：将 RCA 的进位链不断展开，得到
$$\begin{array}{rl}{c}_{i+1}& =g_i+k_i\cdot (g_{i-1}+k_{i-1}\cdot (g_{i-2}+\cdots ))\\ & =g_i+\sum _{j=0}^{i-1}\left(\prod _{l=j+1}^i{k}_l\right)g_j+c_0\prod _{l=0}^i{k}_l\end{array}$$

所以进位信号 $c_{i+1}$ 可以直接根据 $(g_i,k_i)$ 信号计算出来，不必等待 $c_i$ 信号。关键路径长度仅为 $O(\log n)$，但是扇入扇出系数极高。为了平衡计算延迟和电路复杂度，可以使用[分块/分级的超前进位](【硬件算术设计】硬件加法器原理｜第2章：超前进位加法器，分块、分级超前进位加法器 - 知乎 (zhihu.com))。

Parallel-Prefix Adder

并行前缀加法器（PPA）：为了更好的理解 CLA，可以用代数语言描述 $(g_i,k_i)$ 信号的合并过程。我们定义有序对 $(g,k)$ 上的二元运算 $\circ$ 如下：
$$(g_j,k_j)\circ (g_i,k_i):=(g_j+k_j{g}_i,k_i{k}_j)$$

容易验证，它是：结合的、幂等的、不交换的。

那么 CLA 的逻辑表达式可以重写为：
$$\begin{array}{rl}(c_{i+1},k_0{k}_1\cdots k_i)& =(g_i+k_i\cdot (g_{i-1}+k_{i-1}\cdot (g_{i-2}+\cdots )),k_i\cdots k_1{k}_0)\\ & =(g_i,k_i)\circ (g_{i-1},k_{i-1})\circ \cdots \circ (g_0,k_0)\circ (c_0,1)\end{array}$$

其中的每个信号 $(g_i,k_i)$ 和 $(c_0,1)$ 都是立即的。根据二元运算的结合律，可以设计出一族 $(g,k)$ 信号的并行合并网络。Knowles 提出了一类深度最优的并行前缀加法器，电路的构造为：

Knowles Adder 以两种著名的 PPA 为极限：Kogge-Stone Adder, Ladner-Fischer Adder。其中 LF 结构需要无限扇出（适合 FHE 运算），而 KS 结构需要无限并行（乘法数量）。Brent-Kung Adder 通过提升 level 层数（乘法深度）来平衡扇出系数和运算单元数量，还有一些 Hybrid Schemes 混合了 KS, LF, BK 结构。

我们用 Parallel-Prefix Graghs 来简化表示 PPA，每个黑点表示二元运算 $\circ$ 运算（两次乘法，一次加法），运算方向从下往上。不同扇出的 Knowles Adder：

最适合 FHE 运算的 PPA 就是 Ladner-Fischer Adder：我们的软实现不关心扇出系数，重点关注的是乘法深度和乘法数量。

HE library

Double-CRT

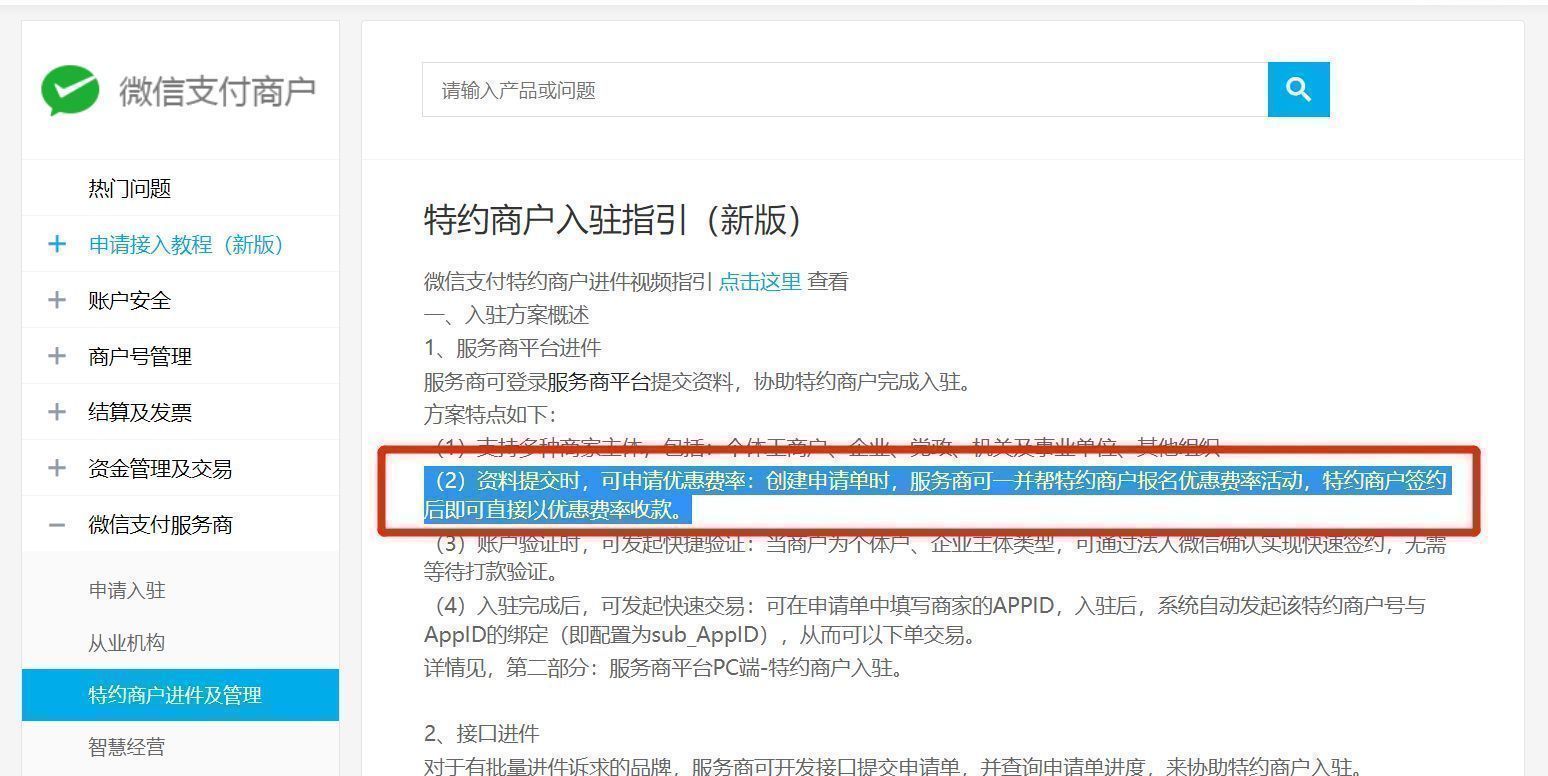
[HS13] 基于 C++ NTL 设计了 RLWE-BGV 的代码实现库 HElib，使用了 [SV11] 的 SIMD 技术，以及 [GHS12] 的 Permuting/Routing 技术。

为了进一步加速，[HS13] 将环 ${\mathbb{Z}}_q[x]/{\varphi }_m(x)$ 中的多项式，表示为了 double-CRT 形式。在 BGV 中使用了 chain of moduli，$q_l={\prod }_{i=0}^l{p}_i$，其中 $p_i$ 是大小近似的素数，并且满足 $m|p_i-1$ 使得 ${\mathbb{Z}}_{p_i}$ 中存在 $m$ 次本原单位根 ${\zeta }_i$，于是 ${\varphi }_m(x)={\prod }_{j\in {\mathbb{Z}}_m^{\ast }}(x-{\zeta }_i^j)(\mathrm{mod}{p}_i)$

我们先对模数 $q_l$ 做 CRT 分解，简记 $R=\mathbb{Z}[x]/{\varphi }_m(x)$，$R_p=R/(pR)$，
$$Z_{q_l}[x]/{\varphi }_m(x)\cong R/(q_{l}R)\cong R/(p_{0}R)\times R/(p_{1}R)\times \cdots \times R/(p_{l}R)$$

然后对于每个小环 $R_{p_i}\cong {\mathbb{Z}}_{p_i}[x]/{\varphi }_m(x)$ 继续做 CRT 分解，
$${\mathbb{Z}}_{p_i}[x]/{\varphi }_m(x)\cong {\mathbb{Z}}_{p_i}[x]/(x-{\zeta }_i^{j_1})\times \cdots \times Z_{p_i}[x]/(x-{\zeta }_i^{j_{\varphi (m)}}),j_t\in {\mathbb{Z}}_m^{\ast }$$

假设 $m=2^k$ 使得 ${\varphi }_m(x)=x^m+1$，那么 Z m ∗ = { 1 , 3 , 5 , ⋯   , m − 1 } \mathbb Z_m^*=\{1,3,5,\cdots,m-1\} Zm∗​={1,3,5,⋯,m−1}，可以使用 FFT/NTT 来快速计算。对于一般的 $m$（混杂的 radix-X），在 ${\mathbb{Z}}_m^{\ast }$ 中的数字分布不规律，系数表示到 Double-CRT 之间的转化较为复杂。

综上，给定模数 $q_l$ 对应 level 的环元素 $a\in Z_{q_l}[x]/{\varphi }_m(x)$，可以表示为矩阵形式：第 $i$ 行是 $a(x)(\mathrm{mod}{p}_i)$ 的 NTT 域，第 $i$ 行第 $j$ 列是元素 $a({\zeta }_i^j)(\mathrm{mod}{p}_i)$，形状 $(l+1)\times \varphi (m)$
D o u b l e C R T l ( a ) = { a ( x ) ( m o d p i ) ( m o d x − ζ i j ) } 0 ≤ i ≤ l ,    j ∈ Z m ∗ = { a ( ζ i j ) ( m o d p i ) } 0 ≤ i ≤ l ,    j ∈ Z m ∗ \begin{aligned} DoubleCRT^l(a) &= \{a(x) \pmod{p_i}\pmod{x-\zeta_i^j}\}_{0\le i\le l,\,\, j\in \mathbb Z_m^*}\\ &= \{a(\zeta_i^j) \pmod{p_i}\}_{0\le i\le l,\,\, j\in \mathbb Z_m^*}\\ \end{aligned} DoubleCRTl(a)​={a(x)(modpi​)(modx−ζij​)}0≤i≤l,j∈Zm∗​​={a(ζij​)(modpi​)}0≤i≤l,j∈Zm∗​​​

容易验证，环元素的加法/乘法，就是矩阵的 component-wise 加法/乘法，
$$\begin{array}{rl}DoubleCR{T}^l(a+b)& =DoubleCR{T}^l(a)+DoubleCR{T}^l(a)\\ DoubleCR{T}^l(a\cdot b)& =DoubleCR{T}^l(a)\cdot DoubleCR{T}^l(a)\end{array}$$

另外 Galois 群 $\mathcal{G}al(\mathbb{Q}(\zeta )/\mathbb{Q})\cong {\mathbb{Z}}_m^{\ast }$ 中的自同构映射为
$${\kappa }_k(a(x)):=a(x^k)(\mathrm{mod}{\varphi }_m(x)),\forall k\in {\mathbb{Z}}_m^{\ast }$$

映射 ${\kappa }_k:\zeta \mapsto {\zeta }^k$ 就等价于：把矩阵 $DoubleCR{T}^l(a)$ 的第 $j$ 列，移动到第 $jk(\mathrm{mod}m)$ 列。所以在 Double-CRT 表示上 Routing 是容易实现的。

New Key Switching in CRT

秘钥切换本质上是关于 $Enc(s)$ 的同态数乘运算 $L_s(c)$，但是密文作为标量的范数相对于模数 $q_l$ 过大，导致同态运算后的噪声项破坏了明文。

在 BGV 中，为了控制秘钥切换的噪声项，使用的是二进制分解方案：给定 $s^{\prime }$ 下的密文 $c^{\prime }$，计算 $c^{\prime }={\sum }_i{2}^i{c}_i^{\prime }$，令
$$c^{\ast }=c_0^{\prime }|c_1^{\prime }|c_2^{\prime }|\cdots ,s^{\ast }=s^{\prime }|2s^{\prime }|4s^{\prime }|\cdots$$

那么计算出矩阵 $W=W[s^{\ast }\to s]$，它满足 $s^{\ast }=W\cdot s$，那么计算密文 $c=c^{\ast }\cdot W$，
$$⟨c^{\prime },s^{\prime }⟩=⟨c^{\ast },s^{\ast }⟩=⟨c,s⟩$$

为了计算 $c^{\prime }$ 的二进制分解，首先需要把 Double-CRT 转换回系数表示。接着，再把 $\log q_l$ 个密文 $c_i^{\prime }$ 分别转化到 Double-CRT 下，以执行解密的内积运算。这花费了 $O(l\log q_l)$ 个长度为 $n=\varphi (m)$ 的 FFT/NTT 运算。

[GHS12] 使用了不同的噪声项控制技术：临时提升模数。使用 LSB 编码方案，假设 $⟨c^{\prime },s^{\prime }⟩=2e^{\prime }+a(\mathrm{mod}q)$，对于任意的奇数 $p$，都有
$$⟨c^{\prime },p{s}^{\prime }⟩=2p{e}^{\prime }+pa=2e^{\prime \prime }+a(\mathrm{mod}pq)$$

其中 $e^{\prime \prime }=p{e}^{\prime }+a(p-1)/2$ 大约是原始噪声 $e^{\prime }$ 的 $p$ 倍。只要执行模切换，回到模数 $q$，那么噪声就基本还是 $e^{\prime }$ 的量级。因此，我们选取充分大的奇数 $p\approx q\sqrt{m}$，使用变换矩阵 $W=W[p{s}^{\prime }\to s]$ 的密文作为秘钥切换辅助。

虽然不需要对 $c^{\prime }$ 做二进制分解了，但是依然需要计算 $c^{\prime }(\mathrm{mod}p)$ 以组成 ${\mathbb{Z}}_{pq}[x]/{\varphi }_m(x)$ 的 Double-CRT 表示。不过因为不需要维度扩展 $\log q_l$ 倍，因此只需要 $O(l)$ 个 FFT/NTT 运算。

注意，因为模数 $pq\ge q^2$，使得 ratio of modulus/noise 变得很大，因此需要将格的维度 $n=\varphi (m)$ 扩大接近两倍，以维持安全强度。但是 FFT/NTT 的复杂度为 $O(n\log n)$，因此计算效率依旧提升了大约 $\log q_l/2$ 因子，同时公钥的存储开销也更低。

也可以混合使用进制分解和提升模数：把密文 $c^{\prime }$ 分解为 ${\sum }_i{D}^i{c}_i^{\prime }$，其中 $D$ 是很大的 radix 使得 $c_i^{\prime }$ 的个数很少；接着，对于每个 $c_i^{\prime }$ 采取临时提升模数的方案。

Modulus Switching in CRT

我们希望除了某些必要的系数表示，将密文和秘钥始终保持在 Double-CRT 表示下，方便快速计算。从模数 $q_l={\prod }_{j=0}^l{p}_j$ 下的密文 $c$ 切换到模数 $q_{l-1}={\prod }_{j=0}^{l-1}{p}_j$ 下的密文 $c^{\prime }$ 时，保持 $c^{\prime }\equiv c(\mathrm{mod}2)$，同时要求 “rounding error” $\tau =c^{\prime }-c/p_t$ 的范数很小。

因为 $p_l$ 是奇素数，这只需计算出 $c^{†}=p_l\cdot c^{\prime }$，使得：$p_l|c^{†}$，$c^{†}\equiv c(\mathrm{mod}2)$，并且 $c^{†}-c$ 的范数很小。然后输出 $c^{\prime }=c^{†}/p_l$ 即可。在 Double-CRT 下的模切换算法为：

1. 从 Double CRT 的最后一行中，计算出 $\bar{c}=c(\mathrm{mod}{p}_l)$ 的系数表示，取值范围 $[-p_l/2,p_l/2)$，但是注意 $\bar{c}$ 属于 $R_{q_l}$
2. 将 $\bar{c}$ 的那些是奇数的系数，通过加减 $p_l$ 变成偶数，取值范围 $[-p_l,p_l)$，得到小多项式 $\delta$，满足 $\delta \equiv c(\mathrm{mod}{p}_l)$ 以及 $\delta \equiv 0(\mathrm{mod}2)$
3. 计算 $\delta$ 的 Double CRT 表示，然后计算出 $c^{†}=c-\delta (\mathrm{mod}{q}_l)$，它满足 $p_l|c^{†}$
4. 对每个 $c^{†}(\mathrm{mod}{p}_j),j<l$，通过计算 $p_l^{-1}\cdot c^{†}(\mathrm{mod}{p}_j)$，获得 $c^{\prime }=c^{†}/p_l$ 的 Double-CRT 表示

上述过程中，step 1 花费了 $1$ 个 INTT，step 3 花费了 $l$ 个 NTT，共计 $O(l)$ 个长度为 $n=\varphi (m)$ 的 FFT/NTT 运算。

WCC

在 Level FHE 的高层应用中，可以使用乘法数量、乘法深度来衡量算法的效率。然而许多工作中，人们往往只关注某一方面，而非综合考量，因此设计出的高级算法并不一定适合在 level FHE 上做计算。

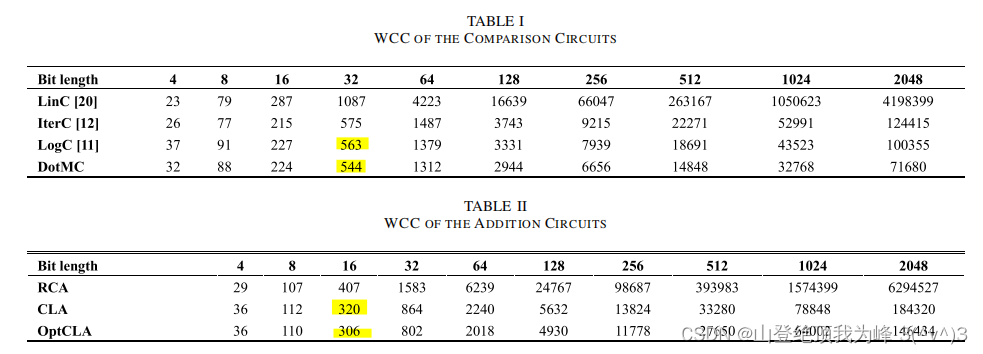
[ZQH+20] 提出了 Weighted Computational Complexity（WCC）计算模型，复杂度定义为
$$WCC=\sum _{l=0}^L{W}_l\cdot N_l$$

其中 $N_l$ 是第 $l$ 层的乘法数量，$W_l$ 是第 $l$ 层的乘法开销（若 $W_l=1,\forall l$ 则只关注乘法数量，若 $W_l=0,l<L$ 则只关注乘法深度）。根据 [GHS12] 的 Double-CRT 下的秘钥切换、模切换，开销为 $O(l)$ 个长度 $n=\varphi (m)$ 的 NTT/FFT 运算。因此，忽略繁复的细节，粗略地选取权重为 $W_l=l+1,l\ge 0$，这是合适的，且足够指导我们设计更加适合 level FHE 的高级算法。

WCC Analysis

[ZQH+20] 分析了整数比较、整数加法的 WCC 复杂度。

三种比较算法，

1. Linear Comparison (LinC)，线性比较
   $$co{m}_i=(a_i\oplus 1)\cdot b_i\oplus (a_i\oplus b_i\oplus 1)\cdot co{m}_{i-1}$$

   最终输出 $COM(A,B)=co{m}_{n-1}$，可计算出 $WCC=O(n^2)$

2. Iteration Comparison (IterC)，分治算法
   $$\begin{gathered} t_{i,1}=(a_i\oplus 1)\cdot b_i,z_{i,1}=a_i\oplus b_i\oplus 1 \\ {t}_{ij}=t_{i+h,j-h}+z_{i+h,j-h}\cdot t_{i,h},j>1,h=\lceil j/2\rceil \end{gathered}$$

   最终输出 $COM(A,B)=t_{0,n}$，它的 WCC 通项公式较为复杂难以写出

3. Logarithm Comparison (LogC)，将线性比较完全展开
   $$\begin{gathered} d_i=(a_i\oplus 1)\cdot b_i,z_i=a_i\oplus b_i\oplus 1 \\ {c}_i=d_i\cdot \prod _{j=i+1}^{n-1}{z}_j \end{gathered}$$

   最终输出 $COM(A,B)={\sum }_{i=0}^{n-1}{c}_i$，使用二叉树计算 ${\prod }_{j=1}^{n-1}{z}_j$，其他的 ${\prod }_{j=i+1}^{n-1}{z}_j$ 是这个二叉树的某些中间结果的乘积（总的乘法数量为 $O(n\log n)$ 而非 $O(n)$）。它的 $WCC=O(n{\log }^{2}n)$

两种整数加法，

1. Ripple-Carry Adder，可计算出 $WCC=O(n^2)$，隐藏的常数比 LinC 更大
2. Parallel-Prefix Adder，可计算出 $WCC=O(n{\log }^{2}n)$，隐藏的常数比 LogC 更大

Dot Multiplication

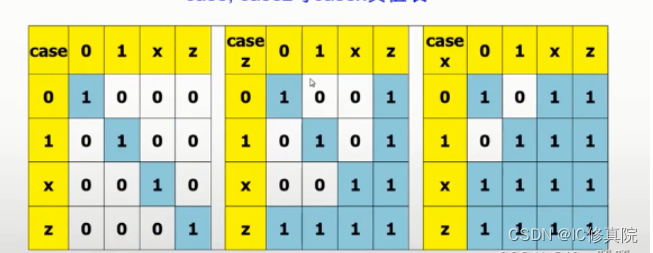
类似于 PPA 的二元运算，[ZQH+20] 定义了 DotMC，
$$(P_1,G_1)\circ (P_0,G_0)=(P_1+G_1\cdot P_0,G_1\cdot G_0)$$

简记 $Add[(P,G)]=P+G$ 是最终信号的合并操作。定义初始信号 $p_i=(a_i\oplus 1)\cdot b_i,0\le i\le n-1$，以及 $g_i=a_i\oplus b_i\oplus 1,1\le i\le n-1$，$g_0=0$，那么有：
$$\begin{array}{rl}COM(A,B)& =(a_{n-1}\oplus 1)\cdot b_{n-1}\oplus (a_{n-1}\oplus b_{n-1}\oplus 1)\cdot co{m}_{n-2}\\ & =Add\left[(p_{n-1},g_{n-1})\circ (p_{n-2},g_{n-2})\circ \cdots \circ (p_0,g_0)\right]\end{array}$$

因为 DotMC 运算是结合的，因此可以使用二叉树方式，并行地合并信号

可以计算出 $WCC=O(n\log n)$，乘法数量 $O(n)$，乘法深度 $O(\log n)$。对比下 LogC 的乘法数量为 $O(n\log n)$，计算复杂度为 $WCC=O(n{\log }^{2}n)$

而 CLA 本身就是使用了 DotMC，不过它的某一些 DotMC 可以延迟计算，平移到更低的 level 上计算，使得 $W_l$ 更小。

原始的 CLA 电路为：

把一些 DotMC 移动（绿色的那些点），

论文指出当 $n>16$ 时，DotMC 的比较和 OptCLA 更加高效，并且随着 $n$ 增大效果更好。