这篇文章我们来讲一下二叉树
目录
1.概述
2.代码实现
1.概述
树:(Tree)是计算机数据存储的一种结构,因为存储类型和现实生活中的树类似所以被称为树。
树的源头被称为根,树其余分叉点被称为节点,而树这种数据结构的起始分叉点被称为根节点。树衍生的尽头就是叶,在树这种数据结构中把叶称之为叶节点。
树中每一节点的起源点被称为父节点,衍生出去的点被称为子节点。没有父节点的就是根节点,没有子节点的就是叶节点,而同一父节点的就是兄弟节点
树的基础概念:
高度,是从下往上看,用来表示从根节点到最顶端叶节点所需要遍历的节点数 (包括叶节点)。
深度与高度相反,是从上往下看,用来表示 从最顶端叶节点到根节点所需要遍历的节点数(包括根节点)。层数,即 高度 +1。
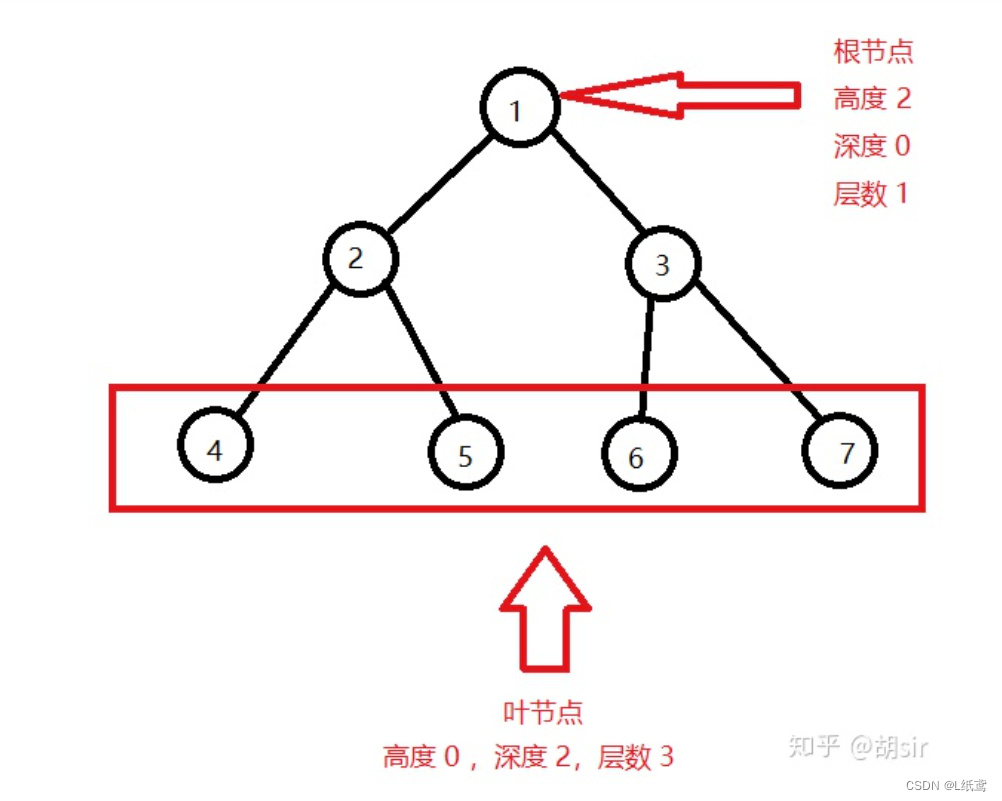
二叉树:是最常用的树形结构,每个结点最多能够有两个子节点。
完全二叉树:上层全部填满,并且最后一层按从左到右的顺序来填充。(前面讲的堆就是一个完全二叉树)
满二叉树:一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树。也就说,如果一个二叉树的结点总数为(2^k)-1,则它就是满二叉树
二叉查找树:所有的左节点值都小于父节点值,所有的右节点值都大于父节点值的二叉树。
注意:这里要注意完全二叉树和满二叉树的区别。
二叉树的实现方式有数组和链表两种实现方式。
下面看一下二叉树的遍历
遍历:即把二叉树的每一个节点都访问一遍。遍历有两种方式,即广度优先和深度优先,其中深度优先又分前序,中序和后序三种,下面来详细的看一下。
广度优先遍历:尽可能的先访问距离根节点最近的节点,也称为层序遍历
深度优先遍历:对于二叉树,深度优先遍历可以分为三种(要深入到叶子节点):
- 前序遍历:对于每一颗子树,先访问该节点,然后是左子树,最后是右子树
- 中序遍历:对于每一颗子树,先访问左子树,然后是该节点,最后是右子树
- 后序遍历:对于每一颗子树,先访问左子树,然后是右子树,最后是该节点
下面用具体的实例来看一下二叉树的几种遍历方式:
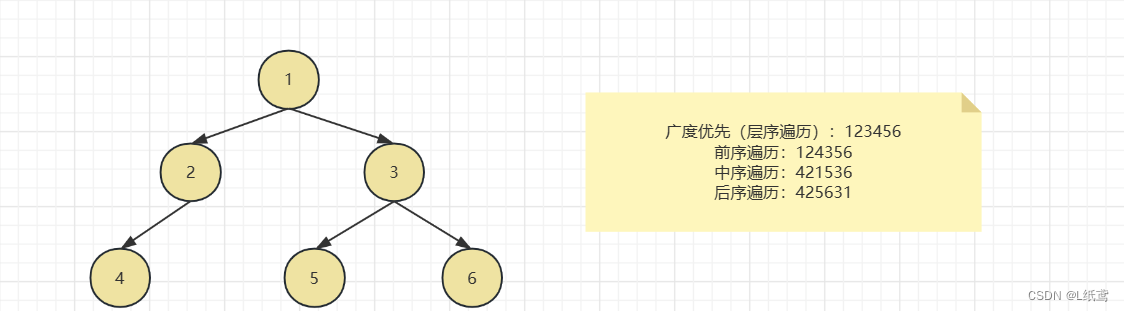
解析:
广度优先,不解释了
前序遍历:前序遍历的定义是先访问该节点,然后是左子树,然后是右子树。就上图来说,首先是根节点即1,然后是左子树,即2这边,在这个子树上面依然按照上面的规则走,所以先是2,然后访问2的左子树,然后是右子树。然后又回到上面的根节点处,现在1的左子树访问完了,然后就访问1的右子树,右子树的访问规则和上面的是一样的。
中序遍历:中序遍历的定义是先访问左子树,然后是根节点,然后是右子树。依然拿上图来说,先访问左子树,即2那部分,然后看2有没有左子树,有,那就访问2的左子树,即4,然后是2,然后是2的右子树,2的那颗树访问完了,就回到根节点,即1,然后再访问1的右子树,逻辑和上面是一样的。这就是中序遍历。
后序遍历:后序遍历的定义是先访问左子树,然后是右子树,然后是根节点。拿上图来说,先访问1的左子树,到达了2后,先访问2的左子树,访问完再访问2的右子树,然后是2,然后回到1处,1的左子树访问完了,然后接着访问1的右子树,等右子树访问完后,最后访问根节点1.
2.代码实现
下面用代码来实现一下树的相关操作:
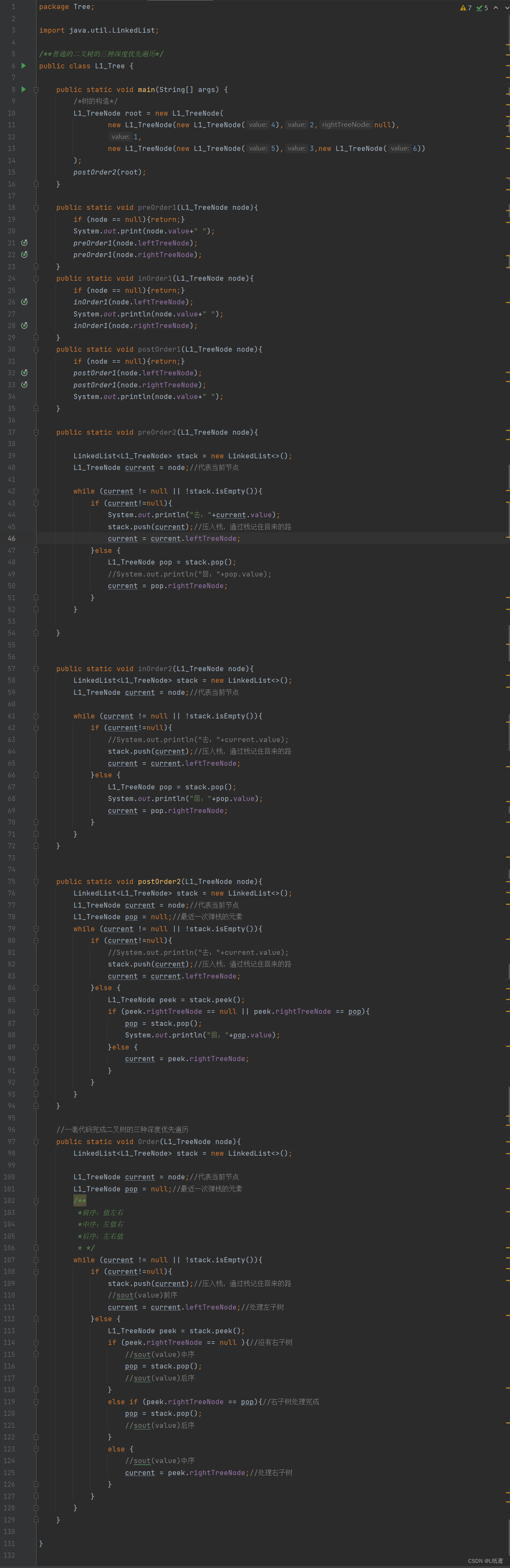
节点类如下:
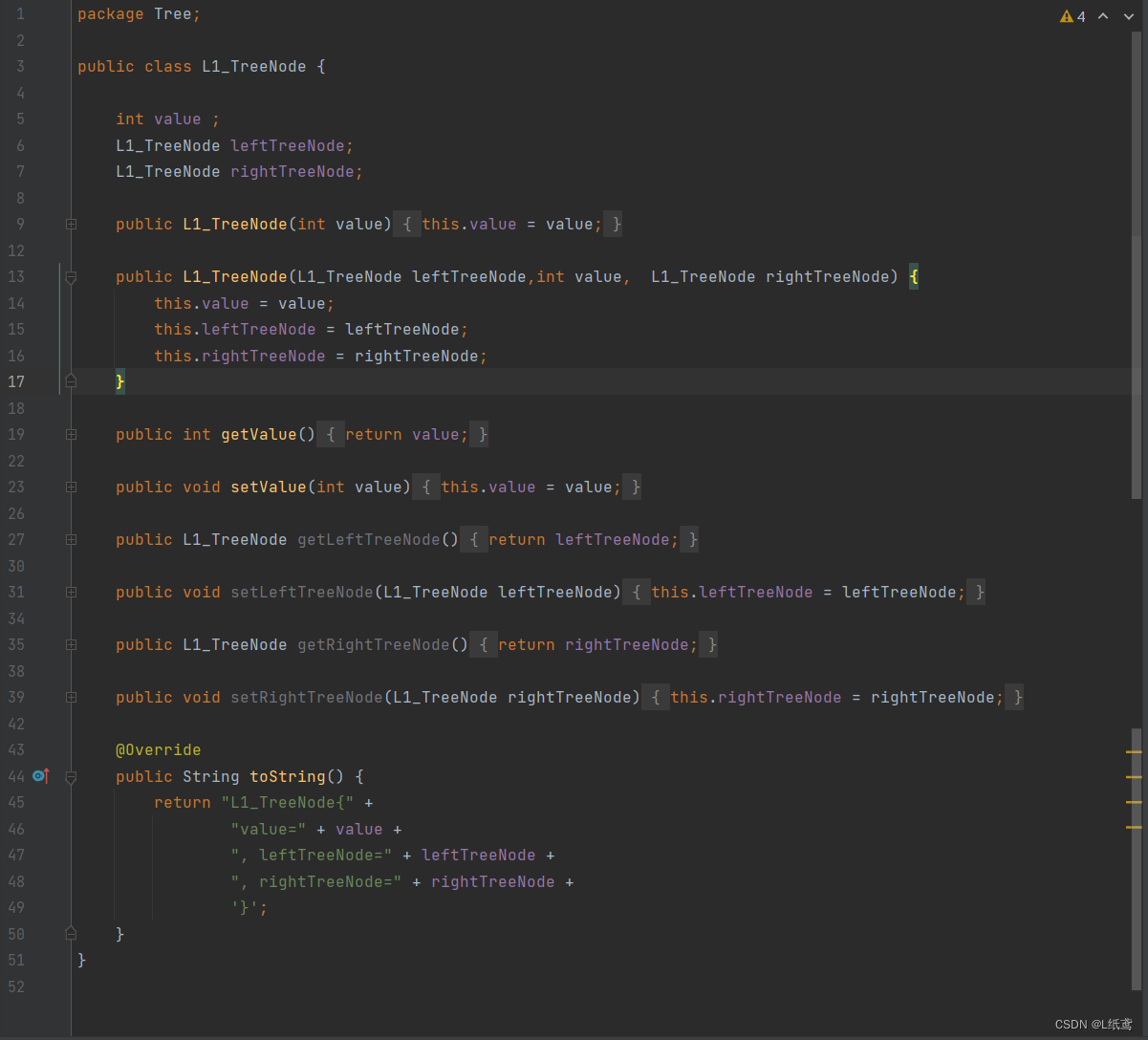
下面看一下代码:
package Tree;
import java.util.LinkedList;
/**普通的二叉树的三种深度优先遍历*/
public class L1_Tree {
public static void main(String[] args) {
/*树的构造*/
L1_TreeNode root = new L1_TreeNode(
new L1_TreeNode(new L1_TreeNode(4),2,null),
1,
new L1_TreeNode(new L1_TreeNode(5),3,new L1_TreeNode(6))
);
postOrder2(root);
}
public static void preOrder1(L1_TreeNode node){
if (node == null){return;}
System.out.print(node.value+" ");
preOrder1(node.leftTreeNode);
preOrder1(node.rightTreeNode);
}
public static void inOrder1(L1_TreeNode node){
if (node == null){return;}
inOrder1(node.leftTreeNode);
System.out.println(node.value+" ");
inOrder1(node.rightTreeNode);
}
public static void postOrder1(L1_TreeNode node){
if (node == null){return;}
postOrder1(node.leftTreeNode);
postOrder1(node.rightTreeNode);
System.out.println(node.value+" ");
}
public static void preOrder2(L1_TreeNode node){
LinkedList<L1_TreeNode> stack = new LinkedList<>();
L1_TreeNode current = node;//代表当前节点
while (current != null || !stack.isEmpty()){
if (current!=null){
System.out.println("去:"+current.value);
stack.push(current);//压入栈,通过栈记住回来的路
current = current.leftTreeNode;
}else {
L1_TreeNode pop = stack.pop();
//System.out.println("回:"+pop.value);
current = pop.rightTreeNode;
}
}
}
public static void inOrder2(L1_TreeNode node){
LinkedList<L1_TreeNode> stack = new LinkedList<>();
L1_TreeNode current = node;//代表当前节点
while (current != null || !stack.isEmpty()){
if (current!=null){
//System.out.println("去:"+current.value);
stack.push(current);//压入栈,通过栈记住回来的路
current = current.leftTreeNode;
}else {
L1_TreeNode pop = stack.pop();
System.out.println("回:"+pop.value);
current = pop.rightTreeNode;
}
}
}
public static void postOrder2(L1_TreeNode node){
LinkedList<L1_TreeNode> stack = new LinkedList<>();
L1_TreeNode current = node;//代表当前节点
L1_TreeNode pop = null;//最近一次弹栈的元素
while (current != null || !stack.isEmpty()){
if (current!=null){
//System.out.println("去:"+current.value);
stack.push(current);//压入栈,通过栈记住回来的路
current = current.leftTreeNode;
}else {
L1_TreeNode peek = stack.peek();
if (peek.rightTreeNode == null || peek.rightTreeNode == pop){
pop = stack.pop();
System.out.println("回:"+pop.value);
}else {
current = peek.rightTreeNode;
}
}
}
}
//一套代码完成二叉树的三种深度优先遍历
public static void Order(L1_TreeNode node){
LinkedList<L1_TreeNode> stack = new LinkedList<>();
L1_TreeNode current = node;//代表当前节点
L1_TreeNode pop = null;//最近一次弹栈的元素
/**
*前序:值左右
*中序:左值右
*后序:左右值
* */
while (current != null || !stack.isEmpty()){
if (current!=null){
stack.push(current);//压入栈,通过栈记住回来的路
//sout(value)前序
current = current.leftTreeNode;//处理左子树
}else {
L1_TreeNode peek = stack.peek();
if (peek.rightTreeNode == null ){//没有右子树
//sout(value)中序
pop = stack.pop();
//sout(value)后序
}
else if (peek.rightTreeNode == pop){//右子树处理完成
pop = stack.pop();
//sout(value)后序
}
else {
//sout(value)中序
current = peek.rightTreeNode;//处理右子树
}
}
}
}
}
递归的很简单
主要就是要了解非递归的解决方案。