题目：

国旗计划

题解

三个技巧：

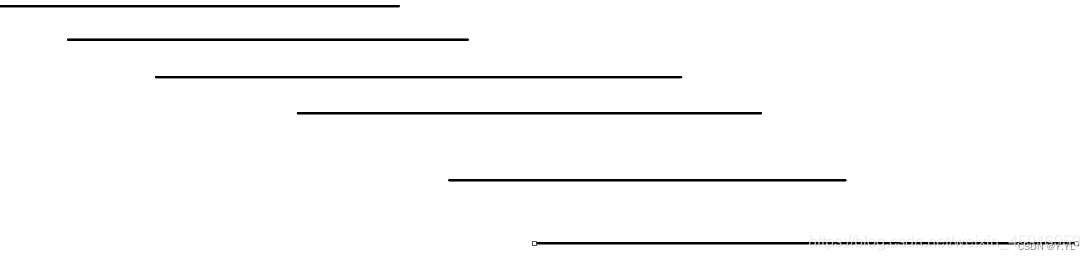
1. 断环成链：
   具体而言就是：

if(w[i].R < w[i].L)
w[i].R += m;
m是环的长度；

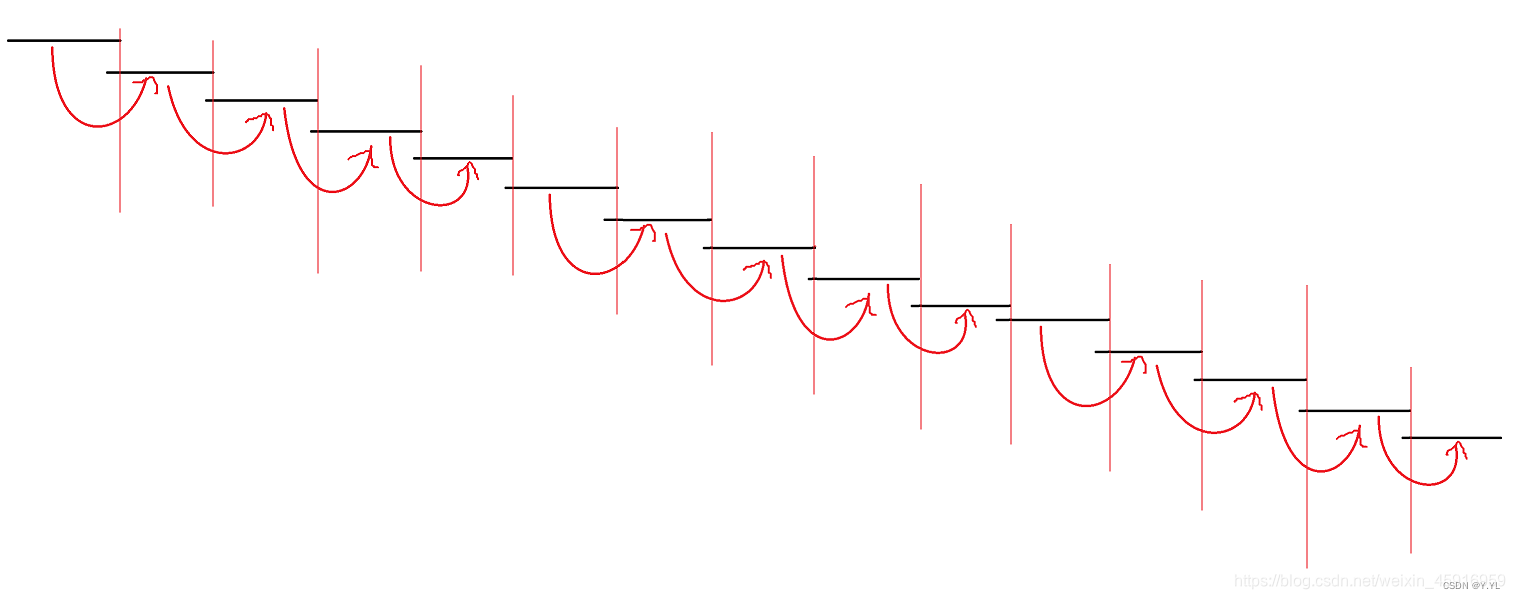
2. 贪心：
   选择一个区间i后，下一个区间只能从左端小于等于i的右端点的区间中选。
   但是每次都往后遍历n次的话，时间复杂度就是O(n²)，超时。
3. 倍增
   为了高效进行查询，参考ST算法，预设好一些“跳板”，快速找到后面的区间。
   定义go[s][i],表示从第s个区间出发，走2ⁱ个最优区间后到达的区间。
   说人话就是：从s到s + 2ⁱ之间，最大的满足条件的左端点的值。
   这个操作的时间复杂度是O(nlogn)。
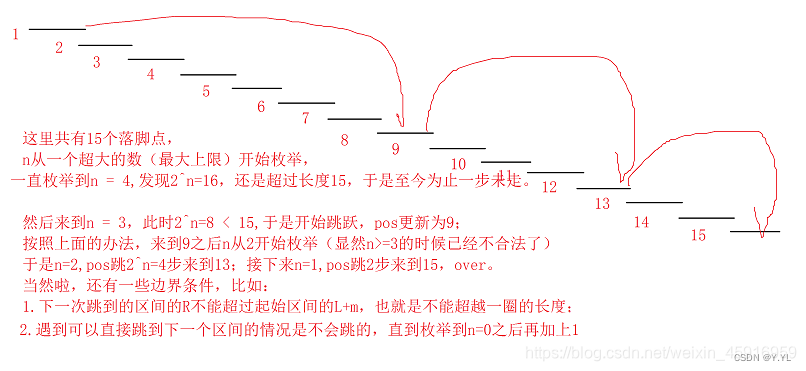
   肝了一个晚上，将自己遇到的几个难点说一下：
   第一个是关于狗函数，我们设从当前区间到下一合法区间为一次，那么我们要跳好多好多次……
   为了简便运算，我们利用倍增的思想进行快速跳跃，狗就是拿来这么用的。

以上所有的操作是O(nlogn) + O(nlogn)次，完全不会超时。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 10;
int n, m;
struct wa
{
    int id, L, R;
}W[maxn * 2];

bool operator < (wa &a, wa &b)
{
    return a.L < b.L;
}

int n2;
//狗函数表示从第s个区间出发，走2^i个区间到达的区间
int go[maxn][20];
//神奇的预处理……尤其是那个什么狗（go）数组，麻烦死了
void init()
{
    //先用nxt找到下一个位置要到哪里？
    int nxt = 1;
    for(int i = 1; i <= n2; i ++)
    {
        //但下一个位置还在范围之内的时候，且下一个位置的L不超过i的R；
        //至于nxt为什么不用刷新，那是因为这个数列具有单调性，无论是L还是R
        while(nxt <= n2 && W[nxt].L <= W[i].R) nxt ++;
        go[i][0] = nxt - 1;
    }
    //长度
    for(int i = 1; (1 << i) <= n; i ++)
        //起点
        for(int s = 1; s <= n2; s ++)
            go[s][i] = go[go[s][i - 1]][i - 1];
}
int res[maxn];
//从第x个战士开始的话，目标战士就一定会被包含在里面了。
void getans (int x)
{
    //len是战士的L加一圈，用来防止R自己跑了一圈，cur是当前战士的位置，ans就是人数咯
    int len = W[x].L + m, cur = x, ans = 1;
    //i从大往小枚举，代表
    for(int i = log2(maxn); i >= 0; i --)
    {
        //然后就是大步大步地跳，跳到的位置没有超过len就是合法的跳
        int pos = go[cur][i];
        //首先往右夸那么多步的区间要存在
        //其次是这个区间的R小于限制
        //最后一点，先不要越过起点的左端点，最后补上；
        //因为我们不确定是不会还有兄贵守着更小的区间，有的话是不能结束的，所以一定要走到i=0。
        if(pos && W[pos].R < len)
        {
            //这中间跳过了2^i个人，要加上。
            ans += 1 << i;
            //然后将标记打到新的人身上。
            cur = pos;
        }
    }
    //最后答案加1
    res[W[x].id] = ans + 1;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++)
    {
        W[i].id = i;
        scanf("%d %d", &W[i].L, &W[i].R);
        //要是R比L小，那就将R加一圈，变成R+m；
        if(W[i].R < W[i].L) W[i].R += m;
    }
    //按照L进行排序，当然，按照R进行排序也可以
    sort(W + 1, W + n + 1);
    n2 = n;
    //拆成链,所有的都往后延长一遍
    for(int i = 1; i <= n; i ++)
    {
        n2 ++;
        W[n2] = W[i];
        W[n2].L = W[i].L + m;
        W[n2].R = W[i].R + m;
    }
    init();
    //逐个计算每个战士。
    for(int i = 1; i <= n; i ++) getans(i);
    for(int i = 1; i <= n; i ++) printf("%d ", res[i]);
    return 0;
}