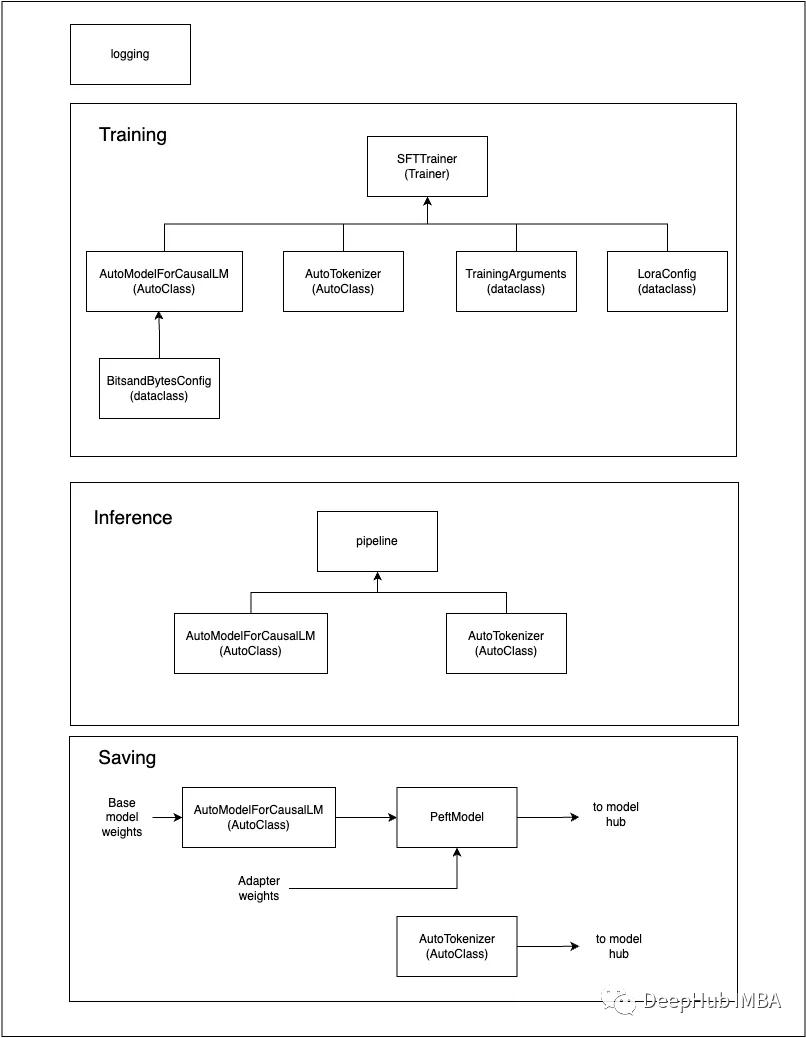
文章目录
- 1.为什么研究角度的编码方式?
- 1.1 角度本身具有周期性
- 1.2 深度学习的损失函数因为角度本身的周期性,在周期性的点上可能产生很大的Loss,造成训练不稳定
- 1.3 那么如何处理边界问题呢:(以θ的边界问题为例)
- 1.3 顺时针(CW)
- 1.4 逆时针(CCW)
- 2 角度回归的方式
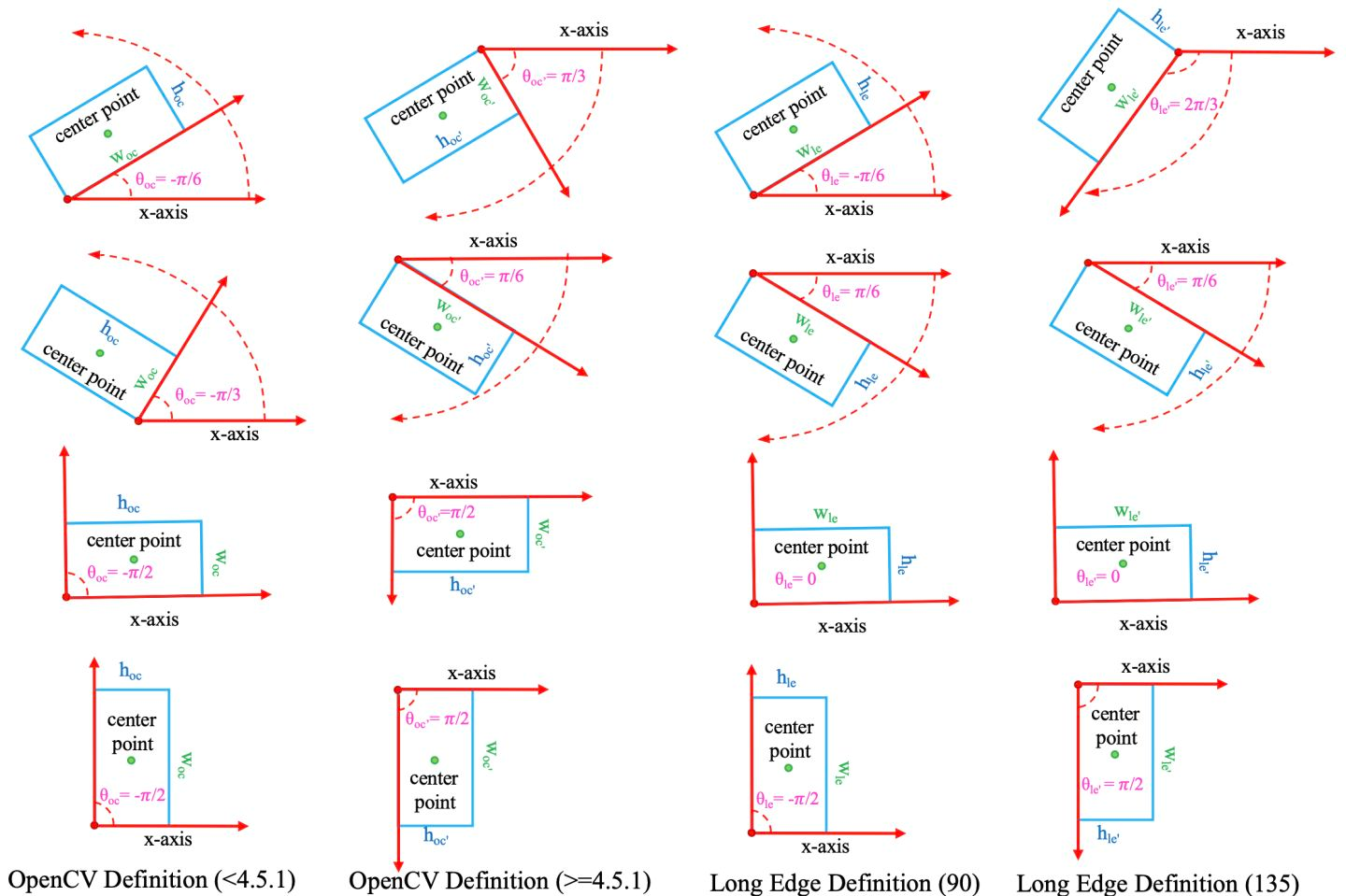
- 2.1 长边定义法,强制W<H,range范围 [-90,+90)
- 2.3 长边定义135度
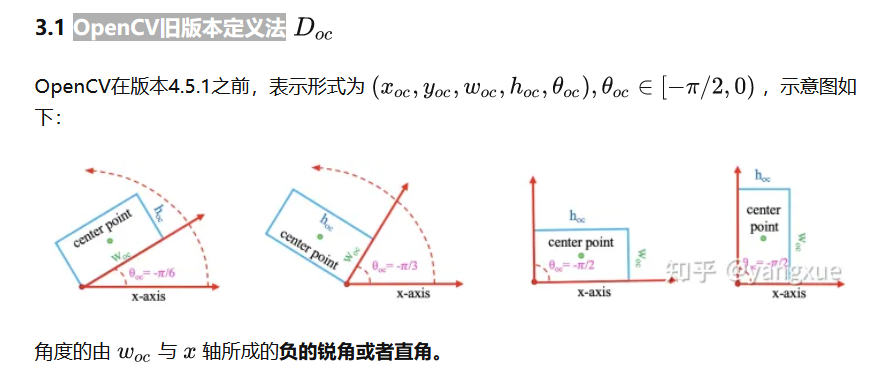
- 2.4 OpenCV旧版本定义法
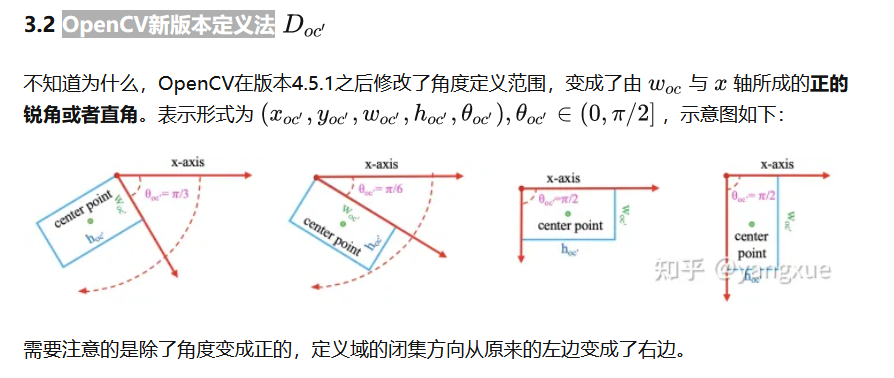
- 2.5 OpenCV新版本定义法
- 不同编码方式之间的转化
- 4 各种表示方法的边界问题
- 参考:
1.为什么研究角度的编码方式?
从框的形式划分,可分为水平检测和旋转检测(即DOTA数据集比赛的task2和task1)。遥感目标检测难点主要包括小目标(small objects)、密集(cluttered arrangement)、方向任意(arbitary orientations)。
1.1 角度本身具有周期性
[ b x , b y , b w , b h , b a n g l e ] [{bx},{by},{bw},{bh},{bangle}] [bx,by,bw,bh,bangle] and [ b x , b y , b w , b h , b a n g l e + π ] [{bx},{by},{bw},{bh},{bangle+π}] [bx,by,bw,bh,bangle+π] 可以表征相同的旋转矩形框
[ b x , b y , b w , b h , b a n g l e ] [{bx},{by},{bw},{bh},{bangle}] [bx,by,bw,bh,bangle] and [ b x , b y , b h , b w , b a n g l e + π / 2 ] [{bx},{by},{bh},{bw},{bangle+π/2}] [bx,by,bh,bw,bangle+π/2] 可以表征相同的旋转矩形框
1.2 深度学习的损失函数因为角度本身的周期性,在周期性的点上可能产生很大的Loss,造成训练不稳定
由于学习的目标参数具有周期性,在周期变化的边界处会导致损失值突增,因此增大网络的学习难度。这句话可以参考下图进行理解:
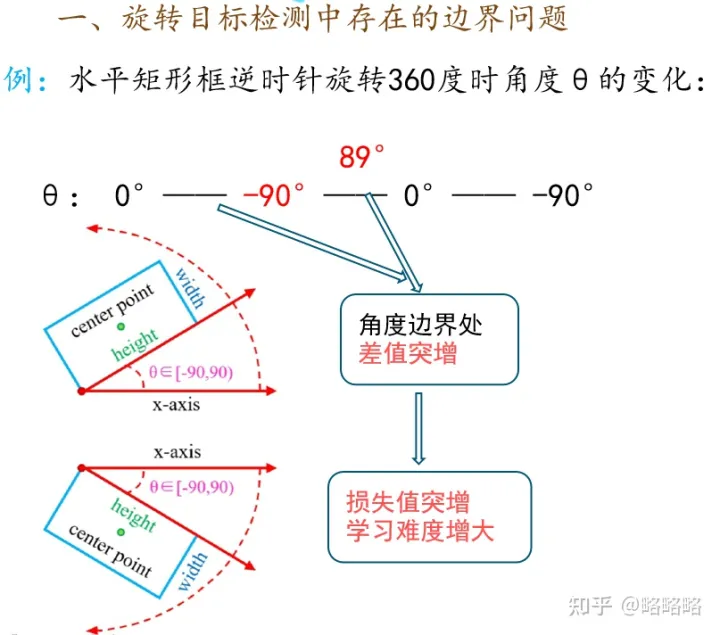
1.3 那么如何处理边界问题呢:(以θ的边界问题为例)
1、寻找一种新的旋转目标定义方式,定义方式中不含具有周期变化性的参数,却又能表示周期旋转的目标物体,根本上杜绝边界问题的产生;(Anchor free/mask的思路,PolarDet、P-RSDet基于极坐标系表示一个任意四边形物体,BBA-Vectors、O^2-DNet基于向量来表示一个有向矩形,ROPDet、Beyond Bounding Box、Oriented Reppoints基于点集来表示一个任意形状的物体,)
2、从损失函数上入手,使用Smooth L1单独考虑每个参数时,赋予损失函数和角度同样的周期性,使得边界处θ之间差值可以很大,但loss变化实际很小;或者综合考虑所有回归参数的影响,使用旋转IoU损失函数也可以规避边界问题,不过RIoU不可导,近似可导的相关工作可以参考KLD、GWD,工程上实现RIoU可导的工作可以参考s2anet/README.md at master · csuhan/s2anet (github.com)
3、θ由回归问题转为分类问题。(把连续问题直接离散化,避开边界情况),当θ变为分类问题后,网络就无法学习到角度距离信息了,比如真实角度为-90,网络预测成89和-89产生的损失值我们期望是一样的,因为角度距离实际上都是1
1.3 顺时针(CW)

1.4 逆时针(CCW)

注:在MMCV中可以设置旋转方向的算子有:box_iou_rotated (默认为CW),nms_rotated (默认为CW),RoIAlignRotated (默认为CCW),RiRoIAlignRotated (默认为CCW)。
2 角度回归的方式
- opencv定义法、
- 长边定义法,
- 四边形定义法
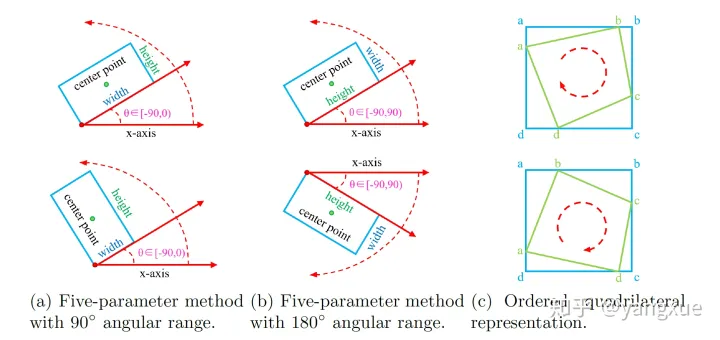

实际上,旋转框既可以由水平框绕在中心点顺时针旋转得到,也可以由水平框绕在中心点逆时针旋转得到。 旋转方向和坐标系的选择密切相关。图像空间采用右手坐标系(y,x) ,其中y轴 是上->下, x轴是左->右。 此时存在2种相反的旋转方向。
2.1 长边定义法,强制W<H,range范围 [-90,+90)

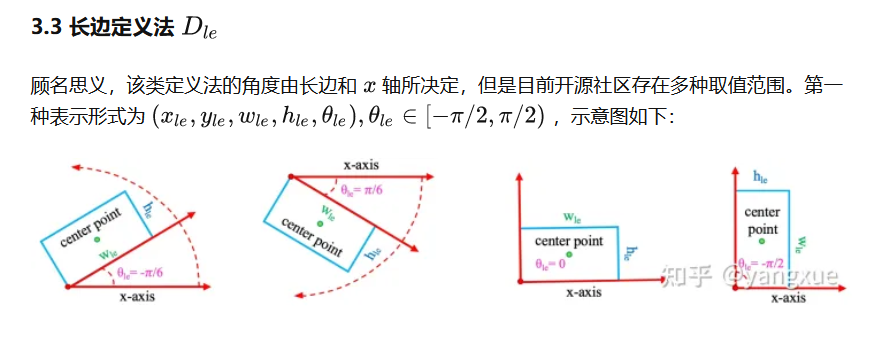
我们采用的是长边定义法,所以我们的注释文件格式为:
[ classid x_c y_c longside shortside Θ ] Θ∈[0, 180)
* longside: 旋转矩形框的最长边
* shortside: 与最长边对应的另一边
* Θ: x轴顺时针旋转遇到最长边所经过的角度
利用好cv2.minAreaRect()函数+总结规律就可以
注意opencv4.1.2版本cv2.minAreaRect()函数生成的最小外接矩形框(x,y,w,h,θ)的几个大坑:
(1) 在绝大数情况下 Θ∈[-90, 0);
(2) 部分水平或垂直的目标边框,其θ值为0;
(3) width或height有时输出0, 与此同时Θ = 90;
(4) 输出的width或height有时会超过图片本身的宽高,即归一化时数据>1。
注意:数据加载器中存在大量的归一化和反归一化的操作,以及大量涉及到图像宽高度的数据变化,因此网络输入的图像size:HEIGHT 必须= WIDTH,因为长边定义法中的longside和shorside与图像的宽高没有严格的对应关系。
数据加载器中涉及三类数据增强方式:Mosaic,random_perspective(仿射矩阵增强),普通数据增强方式。
其中Mosaic,仿射矩阵增强都是针对(X_LT, Y_LT, X_RB, Y_RB)数据格式进行增强,修改时添加θ维度就可以,不过仿射矩阵增强函数内共有 Translation、Shear、Rotation、Scale、Perspective、Center 6种数据增强方式,其中旋转与形变仿射的变换会引起目标角度上的改变。
所以只要超参数中的 [‘perspective’]=0,[‘degrees’]=0 ,这块函数代码就不需要修改逻辑部分,为了方便我们直接把涉及到角度的增强放在最后的普通数据增强方式中。
注意:Mosaic操作中会同时触发MixUp数据增强操作,但是在遥感/无人机应用场景中我个人认为并不适用,首先背景复杂就是该场景中的普遍难题,MixUp会融合两张图像,图像中的小目标会掺杂另一张图的背景信息(包含形似物或噪声),从而影响小目标的特征提取。(不过一切以实验结果为准)
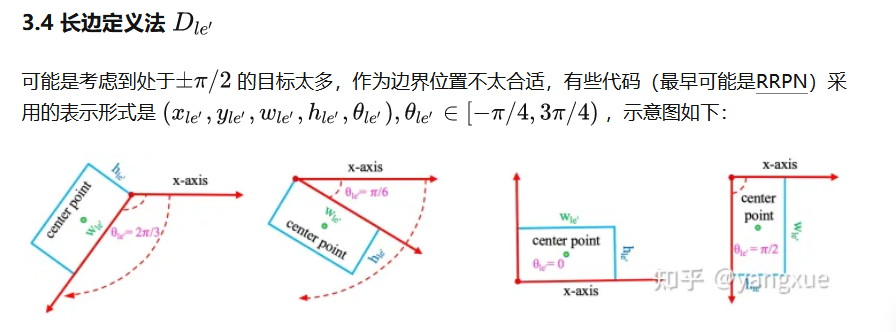
2.3 长边定义135度
2.4 OpenCV旧版本定义法
2.5 OpenCV新版本定义法
不同编码方式之间的转化
查阅
上面只列了三种转换关系,未列的可以通过这三个进行多步转换或者有兴趣的可以自己总结一下转换关系。不管是哪个表示法的转换,我们可以发现当需要进行变换操作的时候一般是这两种:
边进行交换,同时角度加减 pi/2
边不交换,角度加减 pi
这就很有意思,熟悉GWD论文的朋友可能也回想起不同定义法下的边界问题好像也是这两个关系。我们再来回顾一下为什么高斯建模可以统一不同的定义法和边界问题:
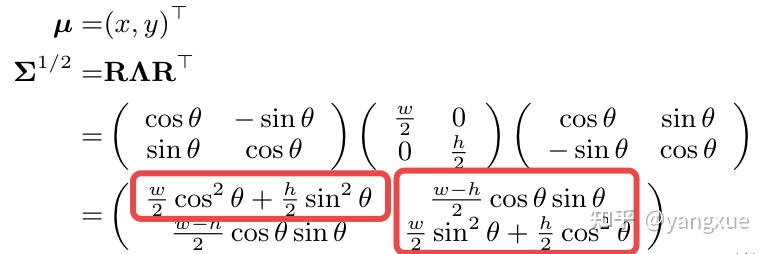
红框中是协方差
中三种不同的元素,这三个元素有一个共同的特点就是经过上面两种变换前后还是相同的,所以高斯建模的优势就在于此。之所以需要三个,那是因为这里有三个参数。抛开高斯分布这个框架,我们是不是可以自己先构造三个这样性质的不同组合,通过直接回归这些参数组合而不是采用GWD和KLD也能成功。
如果再思考得深入一点,我们发现对于不同的表示方式,它们计算IoU的代码其实都是通用的。这是为什么呢?因为IoU的计算过程是和第2节讲的旋转变换有关。在框的旋转过程中我们是不需要考虑旋转角度是怎么定义的,也就不需要担心变换之后是否超过定义范围,逆时针旋转5度对应的就是原始角度减去5度。检测器的参数回归也是这么做的,即使在解码中出现了我们所说的边界问题,其本质还是一个正常的旋转变换。边界问题是针对某一个确定的表示法来说的,因此如果使用IoU损失这种不用考虑框表示方式的损失函数来优化检测器就能完全不用在意边界问题。相同的,高斯建模中的协方差
也存在旋转变换,基于它的回归损失同样不需要考虑定义方式和边界问题。我暂将这种回归损失称为表示方式无关和边界问题免疫。
因此在设计旋转检测器过程中,表示法的作用应该局限于给初始候选框(如anchor)一个初始的表示形式,不能参与回归损失的计算,否则不同表示法和边界问题都会对检测器的优化带来影响,即回归损失应该是表示方式无关和边界问题免疫的。
MMRotate支持 OpenCV、长边135°、长边90° 3 种角度定义法,也支持 DOTA、SSDD、HRSID 3 个遥感数据集。
在OpenMMLab的MMCV中,实现了RiRoIAlignRotated, RotatedFeatureAlign 等高性能旋转框 CUDA 算子,因此 MMRotate 无愧是真正的史上最全、最统一的旋转目标检测算法框架。
4 各种表示方法的边界问题
由于大长宽比的目标对于角度的变化是非常敏感的,因此研究边界问题是比较有意义的。我们希望在边界情况也能预测的比较准确,减少有预测框但是不准被当FP的情况。先给出上面三种定义方法边界问题的描述图:
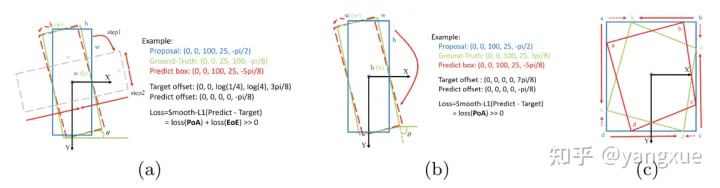
(a)90-regression-based:最理想的角度回归路线是由蓝色框逆时针旋转到红色框,但由于角度的周期性,导致按照这个回归方式的损失非常大(参见上图右边的Example)。此时模型必须以更复杂的形式回归(例如蓝色框顺时针旋转,同时缩放w和h),增加了回归的难度。通过下图(a)右边的example,我们可以发现损失值的突增来源于两部分,一个是角度周期性(periodicity of angular,PoA),另一个是边的交换性(exchangeability of edges,EoE)。
(b) 180-regression-based:相同的,这种方式比上面稍微简单一些,损失值的突增只来源于PoA。
© Point-based: 看©图,如果是蓝框是anchor,红框是ground-truth,那么通过点的排序之后,实际和理想的回归方式是一样的(按照回归的距离定义),都是:

通过上述三种例子的分析,我们不难得出这样的结论:理想的预测结果超出了我们所定义的范围,导致出现边界问题,即产生一个较大的损失值。
参考:
论文:RAPiD Rotation-Aware People Detection in Overhead Fisheye Images
https://zhuanlan.zhihu.com/p/358441134
https://zhuanlan.zhihu.com/p/108185873
https://zhuanlan.zhihu.com/p/111493759