74. 搜索二维矩阵 - 力扣（LeetCode）

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非递减顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

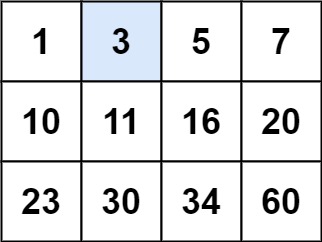
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int matrixSize = matrix.length;
        int matrixColSize = matrix[0].length;
        int len = matrixSize * matrixColSize;
        int right = len - 1;
        int left = 0;
        int mid = 0;
        int row ,col;
        while(left < right) {
            mid = (left+right) / 2;
            row = mid/matrixColSize;
            col = mid%matrixColSize;
            if(matrix[row][col] <= target)  left = mid+1;
            else if(matrix[row][col] > target) right = mid;
        }
        System.out.println(left);
        System.out.println(matrixColSize);
        row = left/matrixColSize;
        col = left%matrixColSize;
        if(matrix[row][col] == target) return true;
        left-=1;
        row = left/matrixColSize;
        col = left%matrixColSize;
        if(left >= 0)
        if(matrix[row][col] == target) return true;
        return false;
    }
}

   

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int matrixSize = matrix.length;
        int matrixColSize = matrix[0].length;
        int row = matrixSize-1;
        while(row >= 0 && matrix[row][0] > target) row-=1;
        if(row < 0 ) return false;
        int left = 0;
        int right = matrixColSize - 1;
        while(left < right) {
            int mid = (left+right) / 2;
            if(matrix[row][mid] > target) right = mid;
            else if(matrix[row][mid] <= target) left = mid+1;
        }
        System.out.println(left);
        System.out.println(row);
        if(matrix[row][left]==target || (left - 1 >= 0&&matrix[row][left-1]==target)) return true; 
        return false;
    }
}

        每日一题，今天是中等题。也是和二分有关。

        这是一道矩阵搜索的题目。从左到右，从上到下是递增的，又是搜索数，所以很快能够想到二分查找。

        那就是怎么二分查找的问题而已了。这里博主给出两种方法。

       第一种：把整个矩阵当作一个大数组，len = row*col。而二维矩阵的列和行地址无非就是除col和模col就可以得到了，那其他地方就当作正常的二分查找就可以了，具体的代码就是第一种方案。

        第二种：由于整个矩阵是递增的，也就是说，最左边的一定是最小的，那只要去比较最左边的数和target的值就可以了，找到最左边数小于target的那一行，那么target要么在那一行，要么就bu'jian