变换点或者变换向量
左乘
矩阵左乘通常是指对”目标点“进行左乘,即:
A
′
=
R
∗
A
A'=R*A
A′=R∗A
其中,A为原始3维点,表示一个3*1的列向量,R为33的旋转矩阵,A‘为变换后的点
B
′
=
T
∗
B
B'=T*B
B′=T∗B
其中,B为原始点3维点,表示一个4*1的齐次化列向量,T为44的旋转矩阵R|t,B‘为变换后的点
以此类推,
如果是点云
c
l
o
u
d
s
r
c
=
{
X
s
r
c
∣
X
s
r
c
=
A
1
,
A
2
…
…
A
n
}
cloud_{src}=\{X_{src}|X_{src}=A_1,A_2……A_n\}
cloudsrc={Xsrc∣Xsrc=A1,A2……An},A表示一个3*1的列向量
此时
X
s
r
c
X_{src}
Xsrc为一个3*n的矩阵,那么变换可以表示为
X
A
′
=
R
∗
X
A
X_A'=R*X_A
XA′=R∗XA
X
B
′
=
T
∗
X
B
X_B'=T*X_B
XB′=T∗XB
矩阵与旋转角
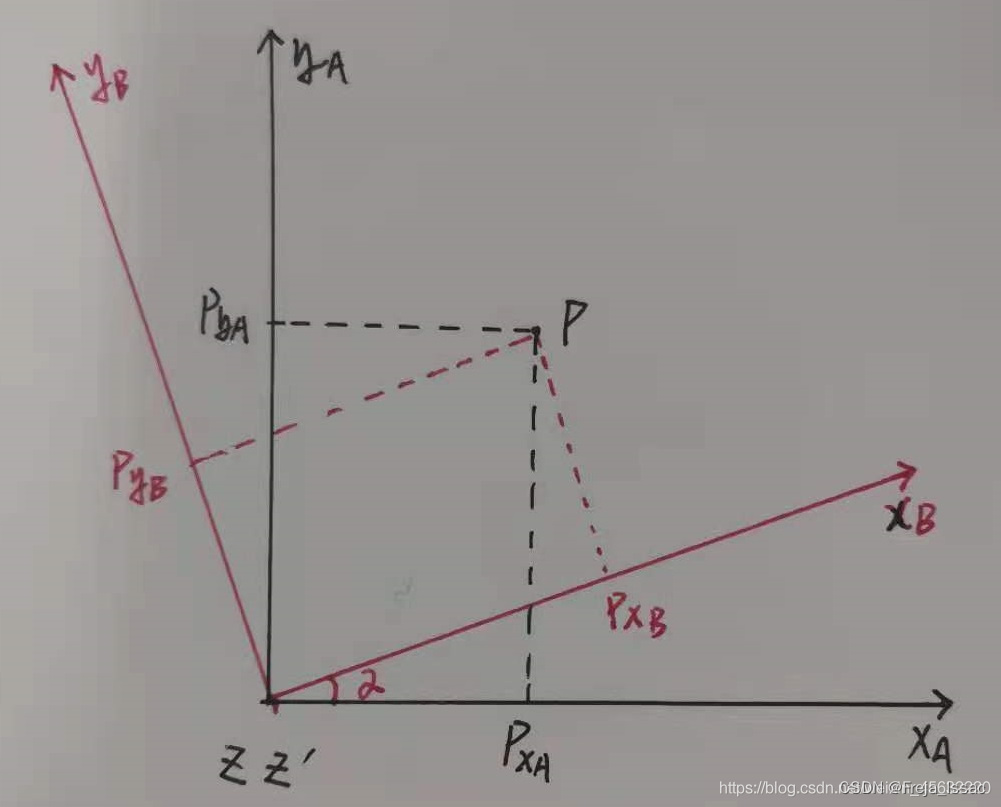
上面为3维点的变换,为了方便画图解释下面以2维点进行描述:
P
A
=
R
∗
P
B
P_A = R*P_B
PA=R∗PB
将矩阵乘法展开可以写为:
[
P
x
A
P
y
A
P
z
A
]
=
[
c
o
s
(
α
)
−
s
i
n
(
α
)
0
s
i
n
(
α
)
c
o
s
(
α
)
0
0
0
1
]
∗
[
P
x
B
P
y
B
P
z
B
]
\begin{bmatrix} P_{xA}\\P_{yA}\\P_{zA} \end{bmatrix} = \begin{bmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix}*\begin{bmatrix} P_{xB}\\P_{yB}\\P_{zB} \end{bmatrix}
PxAPyAPzA
=
cos(α)sin(α)0−sin(α)cos(α)0001
∗
PxBPyBPzB
上面图片表示的是一个矩阵的左乘,其中旋转矩阵R表达的是B点绕z轴逆时针旋转
α
\alpha
α度,得到A点。
如果是旋转一个坐标系的话,那么上面的矩阵表示的就是坐标B系绕Z轴顺时针旋转
α
\alpha
α度,得到A坐标系。
右乘
矩阵左乘通常是指对”目标向量“进行右乘,即:
A
′
=
A
∗
R
A'=A*R
A′=A∗R
B
′
=
B
∗
T
B'=B*T
B′=B∗T
#验证lidar系下的icp匹配结果与mct系下的icp匹配结果相同
# mct系下的icp匹配结果 表达向量
delta_mat_mct = np.array([[0.999725 , -0.023439 , -0.00130324 , -0.127499] ,
[0.0234409 , 0.999724 , 0.00193209 , 0.0205244] ,
[0.00125752 , -0.0019622 , 0.999999 , -0.00368067] ,
[0.0 , 0.0 , 0.0 , 1]])
# lidar系下的icp匹配结果 表达向量
delta_mat_lidar = np.array([[0.999726 , -0.0234405 , 0.00044465 , -0.0937921] ,
[0.0234395 , 0.999723 , 0.00228773 , 0.140559] ,
[-0.000498197 , -0.00227667 , 0.999998 , -0.00616882] ,
[0 , 0 , 0 , 1]])
#之所以不用mct到lidar的完整外参,只用旋转外参Ra,是因为,icp匹配结果是trans可以理解为旋转R+平移向量t。坐标系变化(lidar、mct)可以理解为旋转Ra+平移向量ta,其中两个坐标系下,旋转增量不随坐标系变换而变换icp_mct_R = icp_lidar_R,平移向量t因为坐标系(lidar、mct)不同平移向量t也会不同。
# 又因为平移向量t不受坐标系变化中的ta影响,只受旋转Ra的影响,因此mct2lidar的ta的3个元素置为0
# mct2lidar = np.array([[0.70710678, 0.70710678, 0.0, -1.477],
# [-0.70710678, 0.70710678, 0.0, -0.77],
# [0.0, 0.0, 1.0, -0.66],
# [0.0, 0.0, 0.0, 1.0]])
mct2lidar = np.array([[0.70710678, 0.70710678, 0.0, 0.0],
[-0.70710678, 0.70710678, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
lidar2mct = np.linalg.inv(mct2lidar)
print("mct2lidar : ")
print(mct2lidar)
print("lidar2mct : ")
print(lidar2mct)
print("delta_mat_mct:")
print(delta_mat_mct)
#icp匹配结果是trans可以理解为旋转R+平移向量t,其中icp_mct_R = icp_lidar_R,t是不相等的。t表示的是两个点云变换的结果,是一个向量,并不是一个点,因此要用右乘。
#$B'=BT$ delta_mat_lidar表示位移向量,lidar2mct表示变换矩阵
print(np.dot( delta_mat_lidar,lidar2mct))
print(delta_mat_lidar)
#$B'=BT$
print(np.dot( delta_mat_mct,mct2lidar))
变换矩阵左右乘/旋转矩阵左右乘
与变换某个目标不同,当一个坐标系发生连续变化时,如何描述这个坐标系的最终变换。
例如,先绕x轴顺时针转180度,然后绕z轴顺时针转45,最后绕y轴转30°
这个时候就会出现两种情况:
1.原始坐标系称为a0,先绕x轴(a0的x轴)顺时针转180度得到坐标系a1,然后绕z轴(这个z轴是a0的z轴)顺时针转45得到坐标系a2,最后绕y轴(这个y轴是a0的y轴)转30°
2.原始坐标系称为a0,先绕x轴(a0的x轴)顺时针转180度得到坐标系a1,然后绕z轴(这个z轴是a1的z轴)顺时针转45得到坐标系a2,最后绕y轴(这个y轴是a2的y轴)转30°
也就是,绕固定坐标系旋转还是绕自身坐标系旋转
此时有个口诀
左乘旋转矩阵绕固定坐标系旋转,右乘旋转矩阵绕自身坐标系旋转