【算法】迷宫问题

news2025/1/11 21:09:37

文章目录

  • 前言
  • 1.迷宫问题求解
    • 分步骤求解
    • 代码
  • 2.迷宫最短路径求解
    • 代码

前言

迷宫问题本质就是一个图的遍历问题，从起点开始不断四个方向探索，直到走到出口，走的过程中我们借助栈记录走过路径的坐标。

栈记录坐标有两方面的作用，一方面是记录走过的路径，一方面方便走到死路时进行回溯找其他的通路

1.迷宫问题求解

https://www.nowcoder.com/questionTerminal/cf24906056f4488c9ddb132f317e03bc

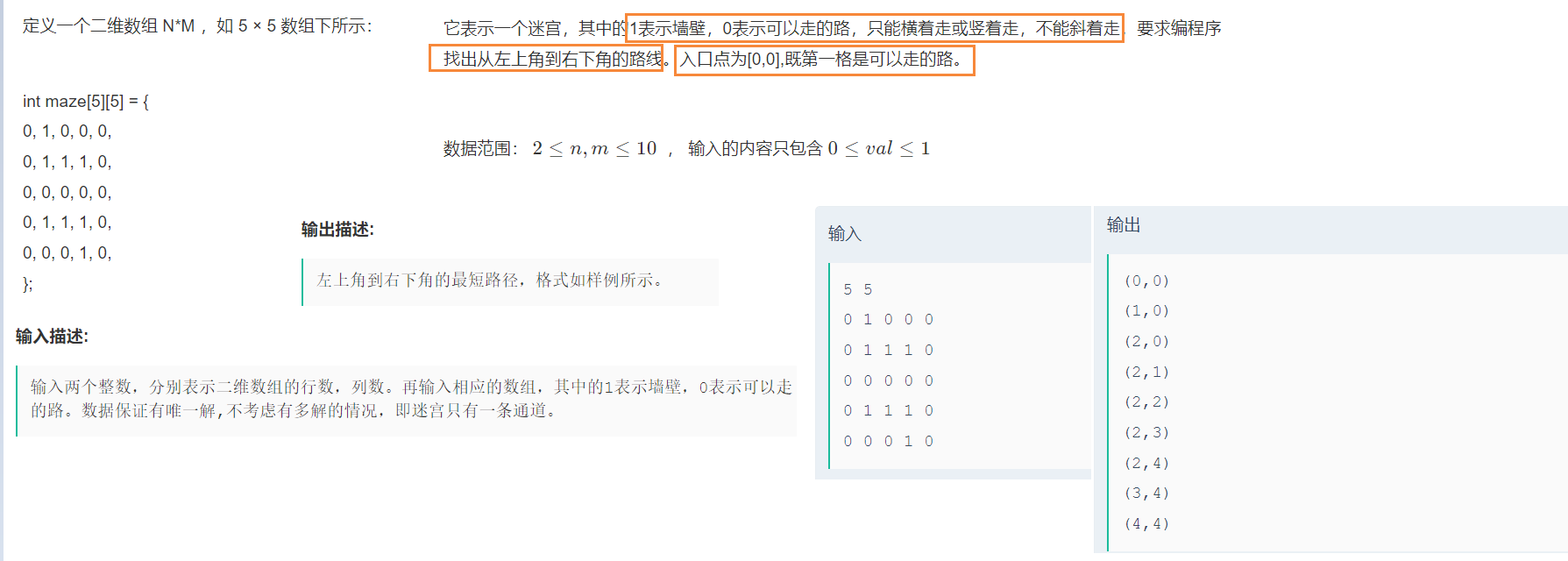
image-20230108211356520

分析

1.此处1表示墙壁不能走，0表示可以走的路

2.(0，0)位置是起点(入口)， (N-1，M-1)是终点(出口)

3.所以思路就是从起点位置开始，向上下左右进行搜索。先判断位置是否合法，如果合法就递归往下继续搜索，不合法则走另一个位置进行搜索。如果四个方向都不合法，那么在保存坐标的容器删除当前位置的坐标。

4.因为是把最近的坐标弹出去，后进先出，所以使用的是栈保存坐标！

5.注意：由于最后输出的是从起点到终点的路径的坐标，栈自底往上才是答案，所以需要把栈的内容倒置过来

思路

0.由于我们要保存坐标的位置，这里可以使用pair，也可以自己定义一个结构体类型进行描述坐标

1.由于可能是循环输入例子，所以使用while(cin >> … )的方式输入N和M，然后开辟N*M的二维数组，输入数据。

2.从起点(0，0)位置开始调用递归函数GetMazePath找通路，题目已经说明了有唯一解！

3.首先要判断方向是否有效，有效才往那个方向走，只要GetMazePath中任意一个方向找到了通路就返回真，如果最后四个方向都不能走，就返回假

C语言如何开辟N*M的二维数组

//方式1：
int maze[N][M] //C99不支持这种方式
//方式2：动态开辟二维数组
int** maze = (int**)malloc(sizeof(int*)*N) //数字共有N个元素，每个元素都是int*(指向一个动态的数组)，首元素的地址为int**  
for(int i = 0 ;i<N;i++)
{
    maze[i] = (int*)malloc(sizeof(int)*M);
}
//释放：先释放一维数组，然后才能释放二维数组，否则就会导致内存泄漏
for(int i = 0;i<N;i++)
{
    free(maze[i]);
    maze[i] = NULL;
}
free(maze);
maze = NULL;

分步骤求解

1.描述位置的结构体定义：

struct Postion
{
    int row;
    int col;
    Postion(int x, int y) :row(x), col(y)
    {}
};

2.定义一个全局的Stack，记录通路上的位置坐标

stack<Postion> Path; //记录通路的路径下标位置

3.输出路径上的坐标的函数 (从起点到终点)

分析：由于Path栈中从栈底到栈顶才是题目要求的输出方式，所以我们需要把Path栈的内容进行倒置

void PrintPath()
{
    //将Path栈中的内容倒置才是输出顺序
    stack<Postion> rPath;
    while (!Path.empty())
    {
        rPath.push(Path.top());
        Path.pop();
    }
    //按格式输出内容
    while (!rPath.empty())
    {
        Postion top = rPath.top();
        printf("(%d,%d)\n", top.row, top.col);
        rPath.pop();
    }
}

4.辅助函数：判断能否往pos位置的方向走

分析：只要保证pos的坐标不是越界的 &&pos位置的值是0（题目说明0是通路）那么就可以往该位置走

bool IsPass(vector<vector<int>>& vv, Postion& pos)
{
    //获取迷宫的行和列
    int N = vv.size();
    int M = vv[0].size();
    //pos位置合法&&pos位置的值是0才是通路，才是可以往pos位置走
    //位置合法：位置的行>=0 && 位置的行<row && 位置的列>=0 && 位置的列<col
    if (pos.row >= 0 && pos.row < N && pos.col >= 0 && pos.col < M
        && vv[pos.row][pos.col] == 0)
        return true;
    else
        return false;
}

5.主递归函数：从cur位置开始往四个方向进行搜索，找通路

分析：先把当前位置坐标放到路径栈当中，然后判断当前位置是不是出口，不是则要往四个方向进行探索！

注意1：我们需要把当前坐标位置的值改为非0值，表示当前位置已经走过了，不走回头路！否则就造成死递归了。当然也可以置为1，因为题目已经说明了1代表的是墙

注意2：往四个方向进行探索，先要检测该方向位置是否合法，只要任一方向找到了通路就可以返回了！因为答案唯一，所以先往哪个方向走的顺序都可以。如果四个方向都找不到通路，说明当前cur位置是无效的位置，需要回溯，把cur位置从栈中弹出。

bool GetMazePath(vector<vector<int>>& vv, Postion cur)
{
    Path.push(cur);//先把当前位置坐标放到路径栈当中
    int N = vv.size();
    int M = vv[0].size();
    if (cur.row == N - 1 && cur.col == M - 1)//判断是否走到出口
        return true;

    vv[cur.row][cur.col] = 2;//把当前位置置成2,或者其它数字也可以，表示已经走过了！

    //往四个方向进行探测，顺序任意，因为答案唯一
    Postion nextUp{ cur.row - 1,cur.col };
    Postion nextDown{ cur.row + 1, cur.col };
    Postion nextLeft{ cur.row, cur.col - 1 };
    Postion nextRight{cur.row, cur.col + 1};

    //先判断能否往该方向走，如果能才往该方向进行下一步探索
    //只要任一方向的探测走到出口就返回真
    if (IsPass(vv, nextUp))//上
    {
        if (GetMazePath(vv, nextUp))
            return true;
    }
    if (IsPass(vv, nextDown))//下
    {
        if (GetMazePath(vv, nextDown))
            return true;
    }
    if (IsPass(vv, nextLeft))//左
    {
        if (GetMazePath(vv, nextLeft))
            return true;
    }
    if (IsPass(vv, nextRight))//右
    {
        if (GetMazePath(vv, nextRight))
            return true;
    }

    //来到这里，说明当前位置往四个方向走都不能得到通路
    Path.pop();//当前位置不是路径上的位置
    return false;
}

6.主函数

分析：定义二维数组，然后输入数据，从起点(0,0)位置开始递归找通路，一定可以找到！然后输出路径上的坐标

int main()
{
    int N, M;
    while (cin >> N >> M)
    {
        vector<vector<int>> maze(N, vector<int>(M));
        for (int i = 0; i < N; i++)
            for (int j = 0; j < M; j++)
                cin >> maze[i][j];

        Postion start{ 0,0 };//起点位置
        if (GetMazePath(maze, start))//从起点位置开始探索找通路
        {
            //找到通路了，输出路径
            PrintPath();
        }
        else
        {
            //没有通路，题目已经说明有唯一解，所以不可能走这里
            cout << "没有通路" << endl;
        }
    }

    return 0;
}

代码

#include<iostream>
#include<vector>
#include<stack>
using namespace std;
struct Postion
{
    int row;
    int col;
    Postion(int x, int y) :row(x), col(y)
    {}
};

stack<Postion> Path; //记录通路的路径下标位置
//输出路径上的坐标 起点->终点
void PrintPath()
{
    //将Path栈中的内容倒置才是输出顺序
    stack<Postion> rPath;
    while (!Path.empty())
    {
        rPath.push(Path.top());
        Path.pop();
    }
    //按格式输出内容
    while (!rPath.empty())
    {
        Postion top = rPath.top();
        printf("(%d,%d)\n", top.row, top.col);
        rPath.pop();
    }
}
//判断能否往pos位置走
bool IsPass(vector<vector<int>>& vv, Postion& pos)
{
    //获取迷宫的行和列
    int N = vv.size();
    int M = vv[0].size();
    //pos位置合法&&pos位置的值是0才是通路，才是可以往pos位置走
    //位置合法：位置的行>=0 && 位置的行<row && 位置的列>=0 && 位置的列<col
    if (pos.row >= 0 && pos.row < N && pos.col >= 0 && pos.col < M
        && vv[pos.row][pos.col] == 0)
        return true;
    else
        return false;
}
//从cur位置开始往四个方向进行搜索，找通路
bool GetMazePath(vector<vector<int>>& vv, Postion cur)
{
    Path.push(cur);//先把当前位置放到路径栈当中
    int N = vv.size();
    int M = vv[0].size();
    if (cur.row == N - 1 && cur.col == M - 1)//判断是否走到出口
        return true;

    vv[cur.row][cur.col] = 2;//把当前位置置成2,或者其它数字也可以，表示已经走过了！

    //往四个方向进行探测，顺序任意，因为答案唯一
    Postion nextUp{ cur.row - 1,cur.col };
    Postion nextDown{ cur.row + 1, cur.col };
    Postion nextLeft{ cur.row, cur.col - 1 };
    Postion nextRight{cur.row, cur.col + 1};

    //先判断能否往该方向走，如果能才往该方向进行下一步探索
    //只要任一方向的探测走到出口就返回真
    if (IsPass(vv, nextUp))//上
    {
        if (GetMazePath(vv, nextUp))
            return true;
    }
    if (IsPass(vv, nextDown))//下
    {
        if (GetMazePath(vv, nextDown))
            return true;
    }
    if (IsPass(vv, nextLeft))//左
    {
        if (GetMazePath(vv, nextLeft))
            return true;
    }
    if (IsPass(vv, nextRight))//右
    {
        if (GetMazePath(vv, nextRight))
            return true;
    }

    //来到这里，说明当前位置往四个方向走都不能得到通路
    Path.pop();//当前位置不是路径上的位置
    return false;
}
int main()
{
    int N, M;
    while (cin >> N >> M)
    {
        vector<vector<int>> maze(N, vector<int>(M));
        for (int i = 0; i < N; i++)
            for (int j = 0; j < M; j++)
                cin >> maze[i][j];

        Postion start{ 0,0 };//起点位置
        if (GetMazePath(maze, start))//从起点位置开始探索找通路
        {
            //找到通路了，输出路径
            PrintPath();
        }
        else
        {
            //没有通路，题目已经说明有唯一解，所以不可能走这里
            cout << "没有通路" << endl;
        }
    }

    return 0;
}

2.迷宫最短路径求解

https://www.nowcoder.com/questionTerminal/571cfbe764824f03b5c0bfd2eb0a8ddf

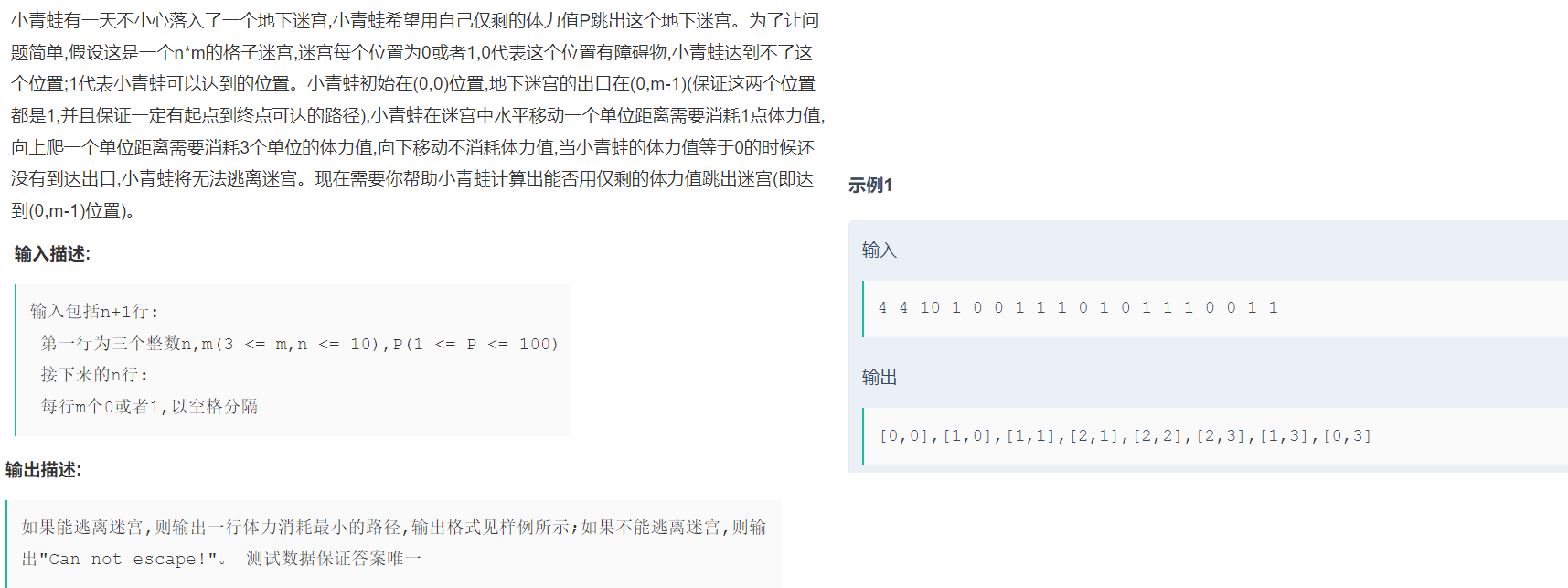
image-20230108225638043

分析：

1.此题中多了体力的限制，向上移动消耗3体力，向下移动不消耗体力值，向左向右消耗1体力

2.并且此时位置的值是0代表的是到不了的位置(可以理解为墙)，位置的值是1表示通路

3.此时的入口是（0，0）位置，出口是（0，m-1）位置(右上角)

4.题目中要求选出体力消耗最小的路径 ，可以理解为求的是最短路径。此时可能没办法逃出迷宫，比如：体力值为负数

所以此处我们要准备两个栈：当前路径栈以及保存答案的栈，需要注意：并不是最短的路径就是答案，因为有体力的消耗，用体力值来过滤路径的合法性

如何找出最优解呢？

把所有的通路都找出来，然后比较，找出最短的路径。此时体力值也是限制选择路径的一个因素！

和上一个题的不同之处

1.此时1代表的是通路，0代表的是墙，所以能否往pos位置走的代码需要变动

if (pos.row >= 0 && pos.row < N && pos.col >= 0 &&pos.col< M&&vv[pos.row][pos.col] == 1)

2.此处的输出格式也有变化

3.1：在GetMazePath函数当中，此时不再需要返回值了，因为此时要找最短的路径，找到了一条通路之后，还需要回溯继续找。

3.2：因为我们是先把当前位置置为2，所以最后四个方向走完回溯的时候，还需要"恢复现场"，把当前位置重新置为1

3.3：由于有体力值的消耗，所以我们要给GetMazePath函数多增加一个体力值的参数

3.4：此时的迷宫出口是右上角位置：(0，M-1)，如果当前位置是出口，那么就判断是否需要更新答案栈，条件为：体力值>=0 && 第一次进入栈为空 || 路径栈的大小 < 答案栈的大小

代码

#include<iostream>
#include<vector>
#include<stack>
using namespace std;
struct Postion
{
    int row;
    int col;
    Postion(int x, int y) :row(x), col(y)
    {}
};

stack<Postion> Path; //记录通路的路径下标位置
stack<Postion> ansPath;//保存最短路径的栈

//输出路径上的坐标 起点->终点
void PrintPath()
{
    //将ansPath栈中的内容倒置才是输出顺序
    stack<Postion> rPath;
    while (!ansPath.empty())
    {
        rPath.push(ansPath.top());
        ansPath.pop();
    }
    //按格式输出内容  最后一个坐标不加, 所以需要分成两部分打印
    //当然也可以在内部判断rPath.size()是否为1，然后打印
    while (rPath.size() > 1)
    {
        Postion top = rPath.top();
        printf("[%d,%d],", top.row, top.col);
        rPath.pop();
    }

    Postion top = rPath.top();
    printf("[%d,%d]", top.row, top.col);
    rPath.pop();
}

//判断能否往pos位置走
bool IsPass(vector<vector<int>>& vv, Postion& pos)
{
    //获取迷宫的行和列
    int N = vv.size();
    int M = vv[0].size();
    //pos位置合法&&pos位置的值是1才是通路，才是可以往pos位置走
    //位置合法：位置的行>=0 && 位置的行<row && 位置的列>=0 && 位置的列<col
    if (pos.row >= 0 && pos.row < N && pos.col >= 0 && pos.col < M
        && vv[pos.row][pos.col] == 1)
        return true;
    else
        return false;
}
//从cur位置开始往四个方向进行搜索，找通路
void GetMazePath(vector<vector<int>>& vv, Postion cur, int P)
{
    Path.push(cur);//先把当前位置放到路径栈当中
    int N = vv.size();
    int M = vv[0].size();
    if (cur.row == 0 && cur.col == M - 1)//判断是否走到出口
    {
        //体力值衡量的是这条路径是否有效
        if (P >= 0 && ansPath.empty() || Path.size() < ansPath.size())
        {
            //更新答案栈
            ansPath = Path;//深拷贝
        }
    }

    vv[cur.row][cur.col] = 2;//把当前位置置成2,或者其它数字也可以，表示已经走过了！

    //往四个方向进行探测，顺序任意，因为答案唯一
    Postion nextUp{ cur.row - 1,cur.col };
    Postion nextDown{ cur.row + 1, cur.col };
    Postion nextLeft{ cur.row, cur.col - 1 };
    Postion nextRight{ cur.row, cur.col + 1 };

    //先判断能否往该方向走，如果能才往该方向进行下一步探索
    if (IsPass(vv, nextUp))//上 ->消耗3体力
        GetMazePath(vv, nextUp,P - 3);

    if (IsPass(vv, nextDown))//下 ->不消耗体力
        GetMazePath(vv, nextDown, P);

    if (IsPass(vv, nextLeft))//左 ->消耗1体力
        GetMazePath(vv, nextLeft, P - 1);

    if (IsPass(vv, nextRight))//右 ->消耗1体力
        GetMazePath(vv, nextRight, P - 1);

    //无论是四个方向都走不通还是已经找到通路
    //都要恢复现场进行回溯 -> 位置置1并且在路径栈弹出当前坐标，继续探索找最短路径
    vv[cur.row][cur.col] = 1;
    Path.pop();
}
int main()
{
    int N, M, P;
    while (cin >> N >> M >> P)
    {
        vector<vector<int>> maze(N, vector<int>(M));
        for (int i = 0; i < N; i++)
            for (int j = 0; j < M; j++)
                cin >> maze[i][j];

        Postion start{ 0,0 };//起点位置
        GetMazePath(maze, start, P);//从起点位置开始探索找通路
        if(!ansPath.empty())//找到最短的通路了，输出路径
           PrintPath();
        else
          cout << "Can not escape!" << endl;
    }

    return 0;
}

为什么这里最后可以直接恢复现场：vv[cur.row][cur.col] = 1呢，会不会把原来0的位置改成1？不会！因为如果vv[cur.row][cur.col] 是0的话，在if判断当中就不能往这个位置走，不会进入递归。所以凡是能进入GetMazePath函数的，其位置的值一定是1

另一种写法

要求的是体力消耗最小的路径，所以我们定义一个变量记录每条通路的体力值，然后比较，满足条件再更新

#include <bits/stdc++.h>

using namespace std;

vector<pair<int, int>> gpath;//迷宫
int max_life = -1; //记录最大体力值
/*
g:记录最终答案  
visited:记录位置是否考察过(记得要恢复现场) 
x和y:当前位置的坐标 
life：剩余体力值path：
path：当前通路上的坐标集合
*/
void dfs(vector<vector<int>> &g, vector<vector<int>> &visited, int x, int y, int life, vector<pair<int, int>> &path) {
    //越界 || 当前位置已经考察过了 || 体力值<0 就返回
    if (x < 0 || x >= g.size() || y < 0 || y >= g[0].size() || g[x][y] == 0 ||visited[x][y] || life < 0) {
        return;
    }
    path.push_back(make_pair(x, y));//保存当前坐标
    
    if (x == 0 && y == g[0].size() - 1)  //迷宫出口
    {
        if (life > max_life)  //当前通路的体力值剩余更多
        {
            gpath = path;
            max_life = life;
        }
        path.pop_back();//在当前通路上的坐标集合中弹出当前坐标，然后继续回溯找
        return;
    }
    
    visited[x][y] = 1;//表示当前位置已经考察过了
    //向四个位置进行搜索
    dfs(g, visited, x - 1, y, life - 3, path);//上
    dfs(g, visited, x + 1, y, life, path);//下
    dfs(g, visited, x, y - 1, life - 1, path);//左
    dfs(g, visited, x, y + 1, life - 1, path);//右
    
    //在当前通路上的坐标集合中弹出当前坐标，然后继续回溯找，并且恢复现场
    path.pop_back();
    visited[x][y] = 0;//恢复现场，没考察过
}

void show_path(vector<pair<int, int>> &path) {
    for (int i = 0; i < path.size(); ++i) {
        cout << '[' << path[i].first << ',' << path[i].second << ']';
        if (i < path.size() - 1) {
            cout << ',';
        }
    }
}

int main() {
    int n, m, life;
    cin >> n >> m >> life;
    
    vector<vector<int>> grids(n, vector<int>(m));
    vector<pair<int, int>> path;
    vector<vector<int>> visited(n, vector<int>(m, 0));
    
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            cin >> grids[i][j];
        }
    }
    dfs(grids, visited, 0, 0, life, path);
    
    if (!gpath.empty()) {
        show_path(gpath);
    } else {
        cout << "Can not escape!" << endl;
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1023740.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java返回日期格式问题

Java返回日期格式问题

Java返回日期格式问题 解决方式&#xff1a; 方式一&#xff1a;在属性上加入注解&#xff0c;对日期进行格式化&#xff0c;每个都要加&#xff0c;比较繁琐。方式二&#xff1a;在WebMvcConfiguration中扩展Spring MVC的消息转换器&#xff0c;统一对日期类型进行格式化处理…
阅读更多...
【第四阶段】kotlin语言的构造函数学习

【第四阶段】kotlin语言的构造函数学习

1.主构造函数 package Kotlin.Stage4 //主构造函数&#xff0c;规范来说&#xff0c;都是增加_xxx的形式&#xff0c;临时的输入类型&#xff0c;不能直接用。需要接收下来&#xff0c;成为变量才能用。 class TestBase(_name:String,_sex:Char,_age:Int,_info:String){ //主…
阅读更多...
浮点数运算精度的问题

浮点数运算精度的问题

每日鸡汤&#xff1a;每个你想要学习的瞬间都是未来的你像自己求救 经典面试题&#xff0c;浮点数运算精度的问题&#xff0c;以前一直没有遇到过&#xff0c;今天可算是遇到了&#xff0c;问题是这样的 有一个需求就是一个商品价值164元&#xff0c;然后有一个8折的优惠券&…
阅读更多...
想要成为一名优秀的测试工程师，必须要遵守这8个测试原则

想要成为一名优秀的测试工程师，必须要遵守这8个测试原则

测试原则是一个测试人员时刻要铭记在心的&#xff0c;甚至要形成一种本能&#xff0c;指导测试工作。 原则1&#xff1a;测试找不出所有的Bug 软件的复杂性仅次于生命体&#xff0c;甚至现在很多软件都已经有了人工智能的属性。对于这样精妙的系统&#xff0c;一小点异常都有可…
阅读更多...
CRM和数字营销什么关系？

CRM和数字营销什么关系？

crm系统是客户管理系统&#xff0c;主要是用来维护和管理客户关系&#xff1b;数字营销是一种营销策略&#xff0c;用来推广产品和服务。 接下来&#xff0c;将为大家带来crm系统和数字营销关系的深度解析&#xff0c;全文干货&#xff01; 一、crm是什么&#xff1f; crm系…
阅读更多...
c++中关于Thread Affinity(线程亲和性)示例源码

c++中关于Thread Affinity(线程亲和性)示例源码

win10下&#xff0c;可以在任务管理器里面设置某个进程的线程亲和性,如下图: 然后选择相关的cpu&#xff0c;如下图&#xff1a; 这么做可以使得相关的线程在某些密集型计算任务中只会运行在某些指定的cpu上&#xff0c;以便提高性能。 以下是windwos上c程序中应用Thread Affi…
阅读更多...
接口自动化测试框架postman tests常用方法

接口自动化测试框架postman tests常用方法

postman常用方法集合&#xff1a; 1.设置环境变量 postman.setEnvironmentVariable("key", "value"); pm.environment.set("key", "value");//postman 5.0以上版本设置环境变量的方法 2.设置全局变量 postman.setGlobalVariable(&…
阅读更多...
numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）

numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）

嗨喽&#xff0c;大家好呀~这里是爱看美女的茜茜呐 &#x1f447; &#x1f447; &#x1f447; 更多精彩机密、教程&#xff0c;尽在下方&#xff0c;赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备好了&#xff0c;直接在文末名片自取就可 点乘和矩阵乘…
阅读更多...
JavaScript中的基础知识挑战

JavaScript中的基础知识挑战

让我们进一步改进史蒂文的小费计算器&#xff0c;这次使用的是循环&#xff01; 创建一个包含所有10个测试账单值的数组 “账单”。为小费和总数创建空数组&#xff08;‘小费’和’总数’&#xff09;。使用我们之前写的’calcTip’函数&#xff08;不需要重复&#xff09;来…
阅读更多...
企业内部安全与风控管理图解

企业内部安全与风控管理图解

企业内部安全说外部安全&#xff0c;企业领导者都非常关注&#xff0c;由于各方面原因&#xff0c;。。。力不从心&#xff0c;妥协&#xff01; 方向&#xff1a; 1、制度 结合企业实情&#xff0c;编制企业安全管理制度 2、硬件 处理常规硬件外观&#xff0c;加壳与锁定、…
阅读更多...
Mybatis工作流程及原理详解

Mybatis工作流程及原理详解

一、概述 1.何为mybatis&#xff1f; MyBatis 是一款优秀的持久层框架&#xff0c;它支持定制化 SQL、存储过程以及高级映射。MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。MyBatis 可以使用简单的 XML 或注解来配置和映射原生信息&#xff0c;将接口和 J…
阅读更多...
计算存储是不是智算时代的杀手锏？

计算存储是不是智算时代的杀手锏？

想象一下&#xff0c;在一个繁忙的数据中心里&#xff0c;有一家大型互联网公司叫做“数据中心的故事”。这家公司一直在使用传统的CPU架构来处理海量数据。但是随着数据量的不断增长&#xff0c;CPU架构遇到了很多问题和瓶颈&#xff0c;这让“数据中心的故事”感到非常苦恼。…
阅读更多...
第一章：最新版零基础学习 PYTHON 教程（第四节 - Python 3 基础知识）

第一章：最新版零基础学习 PYTHON 教程（第四节 - Python 3 基础知识）

Python 3 是一种流行的高级编程语言&#xff0c;用于各种应用程序。以下是您应该了解的一些 Python 3 基础知识&#xff1a; 变量&#xff1a;在 Python 3 中&#xff0c;变量是通过将值分配给名称来创建的。例如&#xff0c;x 5 创建一个名为 x 的变量&#xff0c;并为其分配…
阅读更多...
数据包络分析——SBM模型

数据包络分析——SBM模型

写在前面&#xff1a; 博主本人大学期间参加数学建模竞赛十多余次&#xff0c;获奖等级均在二等奖以上。为了让更多学生在数学建模这条路上少走弯路&#xff0c;故将数学建模常用数学模型算法汇聚于此专栏&#xff0c;希望能够对要参加数学建模比赛的同学们有所帮助。 目录 1. …
阅读更多...
康耐德视觉检测系统可以在元器件生产中发挥什么作用？

康耐德视觉检测系统可以在元器件生产中发挥什么作用？

电子元器件作为电子信息产业链的上游产品&#xff0c;是开发通信、计算机及网络、数字音视频等系统和终端产品的基础&#xff0c;电子元部件工作是否可靠决定了电子设备运行是否正常。电子元器件的外观缺陷检测是一个非常关键的部分&#xff0c;因为这类产品一般都比较小。质量…
阅读更多...
MyBatis 工具学习笔记（基础）

MyBatis 工具学习笔记（基础）

Whats this 是一款优秀的持久层框架&#xff0c;用于简化 JDBC 开发是 Apache 的一个开源项目 Java EE 三层架构&#xff1a;表现层、业务层、持久层&#xff08;存储层&#xff09; &#xff08;持久层&#xff1a;负责将数据保存到数据库的那一层代码&#xff09; ORM&…
阅读更多...
BUUCTF：[MRCTF2020]套娃

BUUCTF：[MRCTF2020]套娃

查看源码发现 PHP非法参数名传参问题&#xff0c;详细请参考我的这篇文章&#xff1a;谈一谈PHP中关于非法参数名传参问题 正则这里绕过使用%0a换行符绕过&#xff0c;payload: /?b.u.p.t23333%0a 得到下一步信息&#xff1a;secrettw.php 注释中的是JsFuck&#xff0c;用这…
阅读更多...
Lostash同步Mysql数据到ElasticSearch（二）logstash脚本配置和常见坑点

Lostash同步Mysql数据到ElasticSearch（二）logstash脚本配置和常见坑点

1. logstash脚本编写&#xff08;采用单文件对应单表实例&#xff09; 新建脚本文件夹 cd /usr/local/logstash mkdir sql & cd sql vim 表名称.conf #如: znyw_data_gkb_logstash.conf 建立文件夹&#xff0c;保存资源文件更新Id mkdir -p /data/logstash/data/last_r…
阅读更多...
VBA技术资料MF58：VBA_测试点是否在多边形中

VBA技术资料MF58：VBA_测试点是否在多边形中

【分享成果&#xff0c;随喜正能量】人一辈子&#xff0c;只能靠长期去做某件事情来成就自己&#xff0c;而不是靠某一个人来成就自己。关于这点&#xff0c;你要么及早领悟&#xff0c;要么等待时光给出教训&#xff0c;逼你领悟。 我给VBA的定义&#xff1a;VBA是个人小型自…
阅读更多...
数据结构 第一章作业 绪论 西安石油大学

数据结构 第一章作业 绪论 西安石油大学

绪论第1章 1&#xff0e;简述下列概念&#xff1a;数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。 答案&#xff1a; 数据&#xff1a;是客观事物的符号表示&#xff0c;指所有能输入到计算机中并被计算机程序处理的符号的总称。如数学计…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023