前言

1、平衡二叉树
2、二叉树的所有路径
3、路径总和||
4、路径总和
5、求根节点到叶节点数字之和

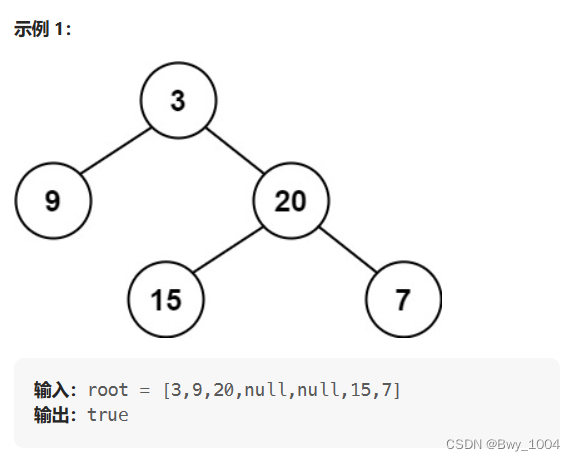
一、平衡二叉树（力扣110）

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
在这里插入图片描述
递归

class Solution {
    /**
    当发现任何一个结点的高度差超过1时，就不是平衡二叉树
     */
    public boolean isBalanced(TreeNode root) {
        int res = getHeight(root);
        if(res==-1)return false;
        else return true;
    }
    public int getHeight(TreeNode node){
        if(node==null) return 0;
        int leftDepth=getHeight(node.left);
        if(leftDepth==-1) return -1;
        int rightDepth=getHeight(node.right);
        if(rightDepth==-1) return -1;

        if(Math.abs(leftDepth-rightDepth)>1) return -1;
        else return 1+Math.max(leftDepth,rightDepth);
    }
}

二、二叉树的所有路径（力扣257）

给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。
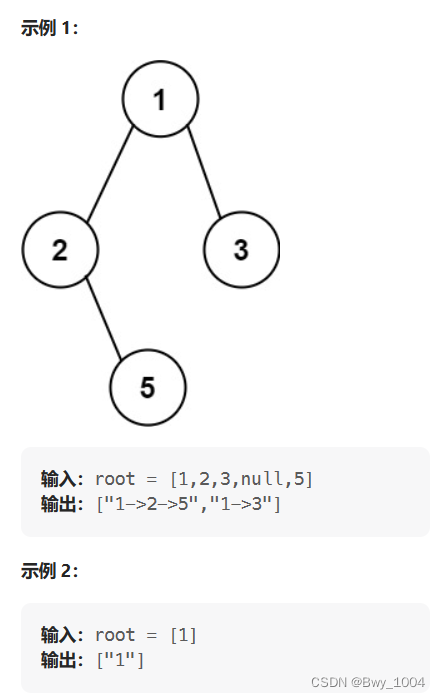
在这里插入图片描述

1、递归法

一图胜千言
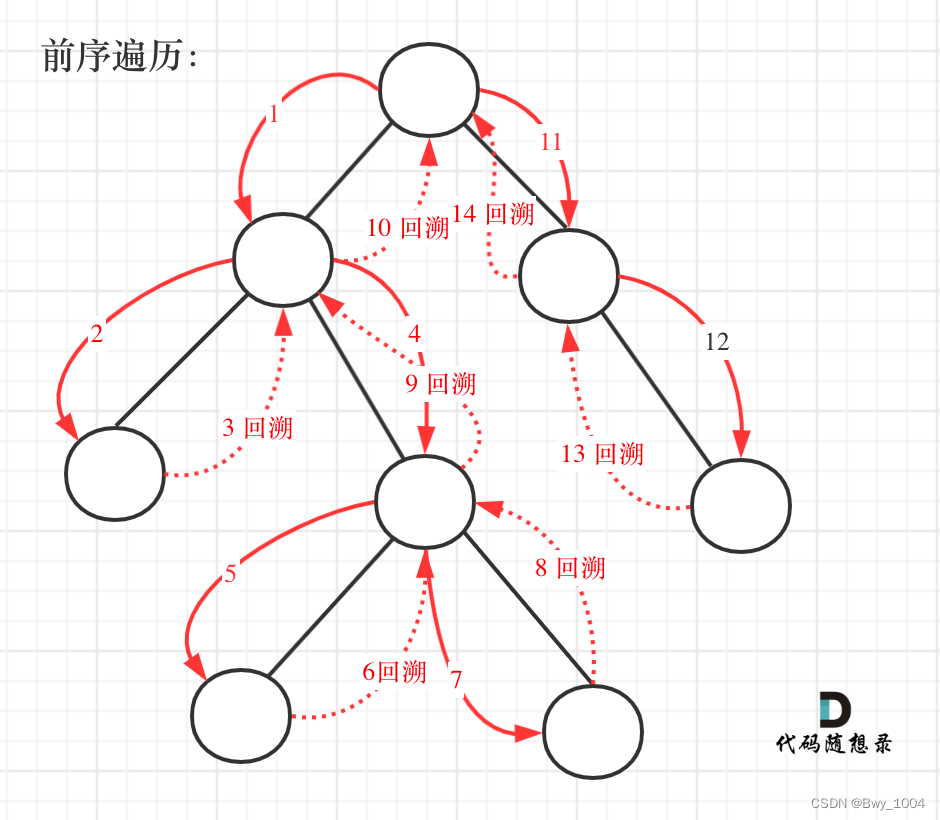
在这里插入图片描述

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        //递归法
        List<String> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        List<Integer> paths = new ArrayList<>();
        traversal(root,paths,res);
        return res;
    }
    public void traversal(TreeNode root,List<Integer> paths,List<String> res){
        //添加结点 （最后叶子节点还没上车）
        paths.add(root.val);
        if(root.left==null && root.right==null){ //叶子节点
            StringBuilder sb = new StringBuilder();
            for(int i = 0;i<paths.size()-1;i++){
                sb.append(paths.get(i)).append("->"); //这条路径遍历结束
            }
            sb.append(paths.get(paths.size()-1));
            res.add(sb.toString());//收为结果集
            return ;
        }
        if(root.left!=null){
            traversal(root.left,paths,res);
            paths.remove(paths.size()-1); //回溯
        }
        if(root.right!=null){
            traversal(root.right,paths,res);
            paths.remove(paths.size()-1); //回溯
        }
    }
}

2、迭代法

非递归的方式，我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        //迭代法 前序遍历 根左右
        List<String> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        Stack<Object> stack = new Stack<>();
        stack.push(root);
        stack.push(root.val+"");
        while(!stack.isEmpty()){
            String path = (String)stack.pop();
            TreeNode node = (TreeNode)stack.pop();
            if(node.left==null&&node.right==null){
                res.add(path);
            }

            if(node.right!=null){
                stack.push(node.right);
                stack.push(path+"->"+node.right.val);
            }
            if(node.left!=null){
                stack.push(node.left);
                stack.push(path+"->"+node.left.val);
            }
        }
        return res;
    }
}

在这里插入图片描述

三、路径总和 II（力扣113）

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。
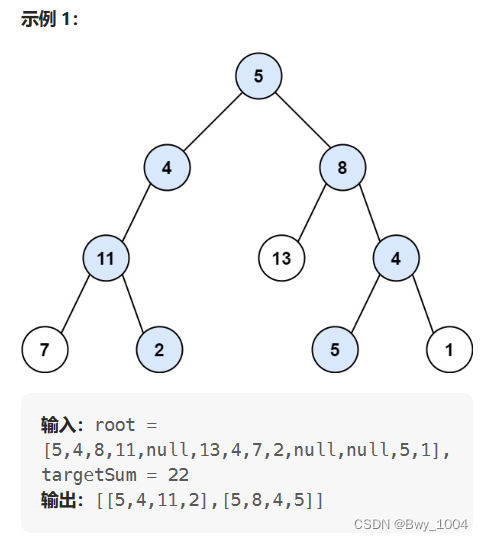
在这里插入图片描述
思路：
与求二叉树的所有路径这道题目类似

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        //递归法
        List<List<Integer>> res = new ArrayList<>();
        if(root==null){
            return res;
        } 
        List<Integer> paths = new ArrayList<>();
        traversal(root,paths,res,targetSum);
        return res;
    }
    public void traversal(TreeNode root,List<Integer> paths,List<List<Integer>> res,Integer targetSum){
        paths.add(root.val);
        if(root.left==null && root.right==null){
            int sum=0;
            List<Integer> item = new ArrayList<>();
            //叶子节点 收集结果
            for(int i=0;i<paths.size();i++){
                sum +=paths.get(i);
                item.add(paths.get(i));
            }
            if(sum==targetSum){
                res.add(item);
            }
            return ;
        }
        if(root.left!=null){
            traversal(root.left,paths,res,targetSum);
            paths.remove(paths.size() - 1);// 回溯
        }
        if(root.right!=null){
            traversal(root.right,paths,res,targetSum);
            paths.remove(paths.size() - 1);// 回溯
        }
    }
}

在这里插入图片描述

四、路径总和（力扣112）

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
在这里插入图片描述
思路：
比第三题更简单一些

class Solution {
    int res = 0;
    public boolean hasPathSum(TreeNode root, int targetSum) {

        if(root==null){
            return false;
        }
        List<Integer> paths = new ArrayList<>();
        traversal(root,paths,targetSum);
        return res>0 ? true : false;
    }
    public void traversal(TreeNode root,List<Integer> paths,int targetSum){
        paths.add(root.val);
        if(root.left==null&&root.right==null){
            int sum = 0;
            //到了叶子结点 收集结果
            for(int i = 0;i<paths.size();i++){
                sum += paths.get(i);
            }
            if(sum==targetSum) res++;
        }
        if(root.left!=null){
            traversal(root.left,paths,targetSum);
            paths.remove(paths.size()-1); //回溯
        }
        if(root.right!=null){
            traversal(root.right,paths,targetSum);
            paths.remove(paths.size()-1); //回溯
        }
    }
}

在这里插入图片描述

五、求根节点到叶节点数字之和（力扣129）

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的所有数字之和。
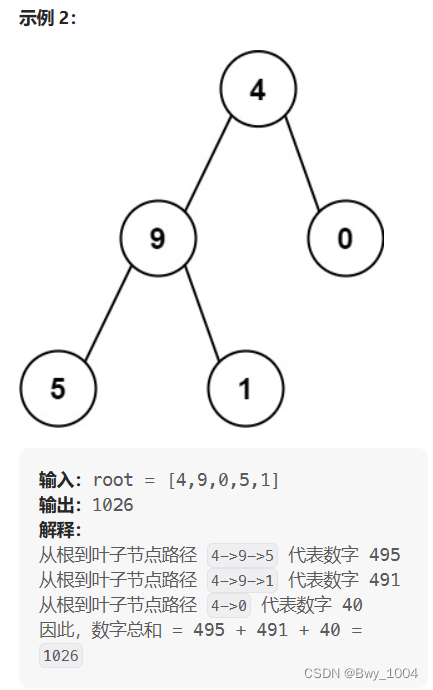
在这里插入图片描述
思路：
需要注意的点就是整条路径上的值求和这个函数功能实现

class Solution {
    List<Integer> paths = new ArrayList<>();
    int res = 0;
    public int sumNumbers(TreeNode root) {
        if(root==null) return 0;
        paths.add(root.val);
        traversal(root);
        return res;


    }
    public void traversal(TreeNode root){
        if(root.left==null && root.right==null){
            res += listToInt(paths);
            return ;
        }
        if(root.left!=null){
            paths.add(root.left.val);
            traversal(root.left);
            paths.remove(paths.size()-1);//回溯
        }
        if(root.right!=null){
            paths.add(root.right.val);
            traversal(root.right);
            paths.remove(paths.size()-1);//回溯
        }
        return ;
    }
    public int listToInt(List<Integer> path){
        int sum = 0;
        for(Integer num:path){
            sum = sum*10+num;
        }
        return sum;
    }
}