快乐数

寻找快乐数

编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为：
对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true ；不是，则返回 false 。

各位数字上的平方之和再相加，最后如果得到了数字1，则这个数字就是快乐数，否则就不是。

快乐数具有以下的特性：

数字满足条件，每位的数字平方后相加，最后的结果是1
最后结果无法等于1，会进入循环。

数字有没有可能会无限大且没有循环？
答：不可能。
例如数字： 2147483648，把他每一位拆分计算后：它肯定就会变成一个三位的数字，因此它不可能无限大下去，它一定会有一个循环或者最后结果为1.

方法一：
利用哈希集和统计计算的每一次的结果，如果陷入了循环，则哈希集合将显示为已经存在，因此此时就可以退出循环，即最后的结果为false；如果结果为1，则结束循环，返回true。

class Solution {
public:
    int getnum(int n)
    {
        int sum=0;
        while (n)
        {
            sum+=(n%10) * (n%10);
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int> s;
        while (n!=1 && !s.count(n))
        {
            s.insert(n);
            n=getnum(n);
        }
        return n==1;
    }
};

方法二：
利用快慢指针，又叫龟兔赛跑法。

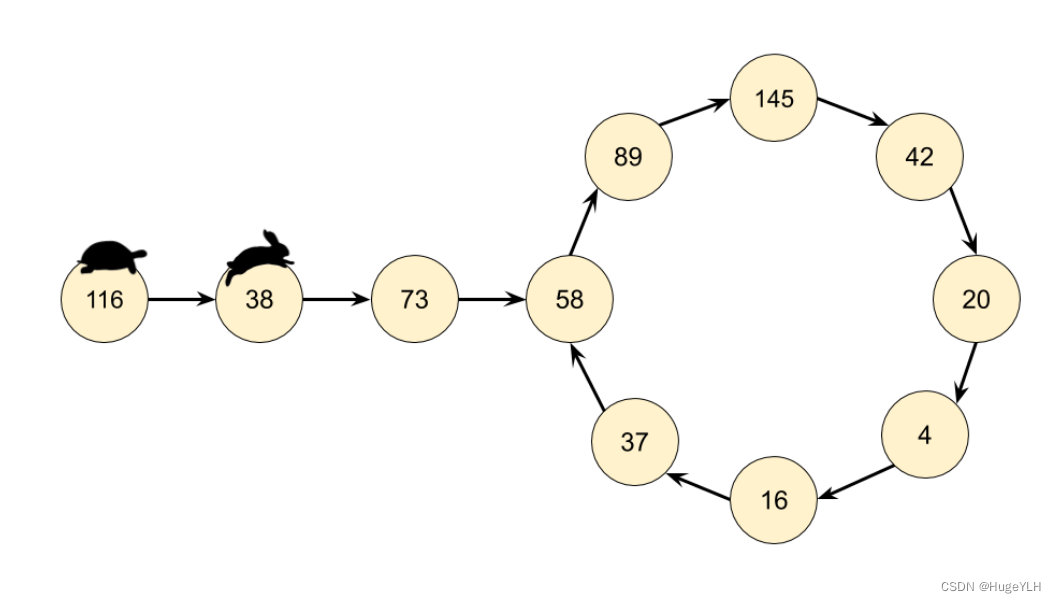
在这里插入图片描述

一个快指针，一个慢指针。
快指针每次走两步，慢指针一次走一步，当他们最后陷入循环的时候，快指针总是能追上慢指针。
快指针自开始后必须每次都快于慢指针两步
快指针为1，则结果为1，返回true
快指针如果进入了循环，则它一定会等于慢指针，因此当他们相等的时候，循环结束，返回false。

class Solution {
public:
    int getnum(int n)
    {
        int sum=0;
        while (n)
        {
            sum+=(n%10) * (n%10);
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow=n;
        int fast=getnum(n);
        while (fast!=1 && fast!=slow)
        {
            slow=getnum(slow);
            fast=getnum(getnum(fast));
        }
        return fast==1;
    }
};

环形链表

给你一个链表的头节点 head ，判断链表中是否有环。
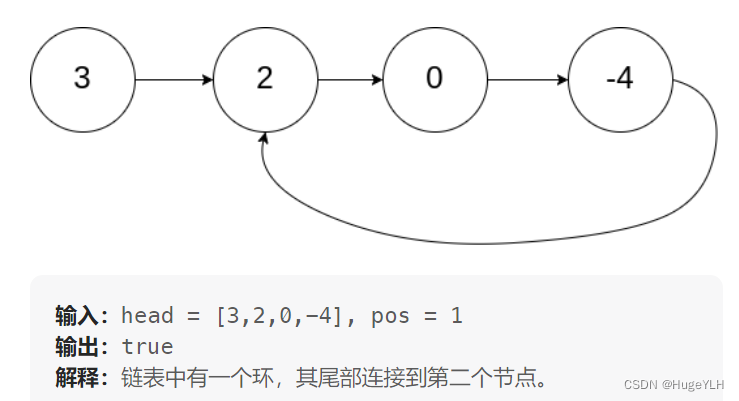
在这里插入图片描述
对于循环链表，我们也采用这种循环检测的算法，即双指针或者哈希集合的方式：

首先来哈希集和：

利用哈希集合来存储每一个节点，如果在之后遍历到的节点的存在于哈希集合中，则结束循环，此链表是环形的。
如果一直遍历到了空节点，则不是环形的。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> s;
        ListNode* p=head;
        while (p!=nullptr && !s.count(p))
        {
            s.insert(p);
            p=p->next;
        }
        return p!=nullptr;
    }
};

方法二：
快慢指针法：

快指针每次走两步，慢指针每次走一步，快指针必须领先于慢指针两步。
快指针在某时刻碰见了慢指针，则是环形的，否则如果快指针到了nullptr，则不是环形的。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (!head || !head->next)
        {
            return false;
        }
        ListNode* pfast=head->next;
        ListNode* pslow=head;
        while (pfast!=nullptr && pfast!=pslow)
        {
            pslow=pslow->next;
            pfast=pfast->next;
            if (pfast!=nullptr)
            {
                pfast=pfast->next;
            }
        }
        return pfast!=nullptr;
    }
};

环形链表II

我们利用双指针或者哈希集合能够很轻松的检测到是否有循环发生，以及何时退出循环，但是我们该如何返回刚进入循环时的第一个节点呢？

使用哈希集和可以很轻松的解决这个问题

哈希集和存储每一个节点
遍历到了已存在于哈希集和中的节点，则它就是循环的入口节点，直接返回就好

我们如果使用双指针，该如何获得链表得入口节点呢？？

这还不简单，当快指针等于慢指针得时候，定义一个临时得节点，然后让他走到快指针的位置，返回这个位置，不就是这个入口节点吗？

大家仔细想一想，快慢指针的相遇不一定是在入口节点发生的，有可能在循环的圈内，因此返回快指针的位置是完全错误的。。

我们首先来整理一下思路：
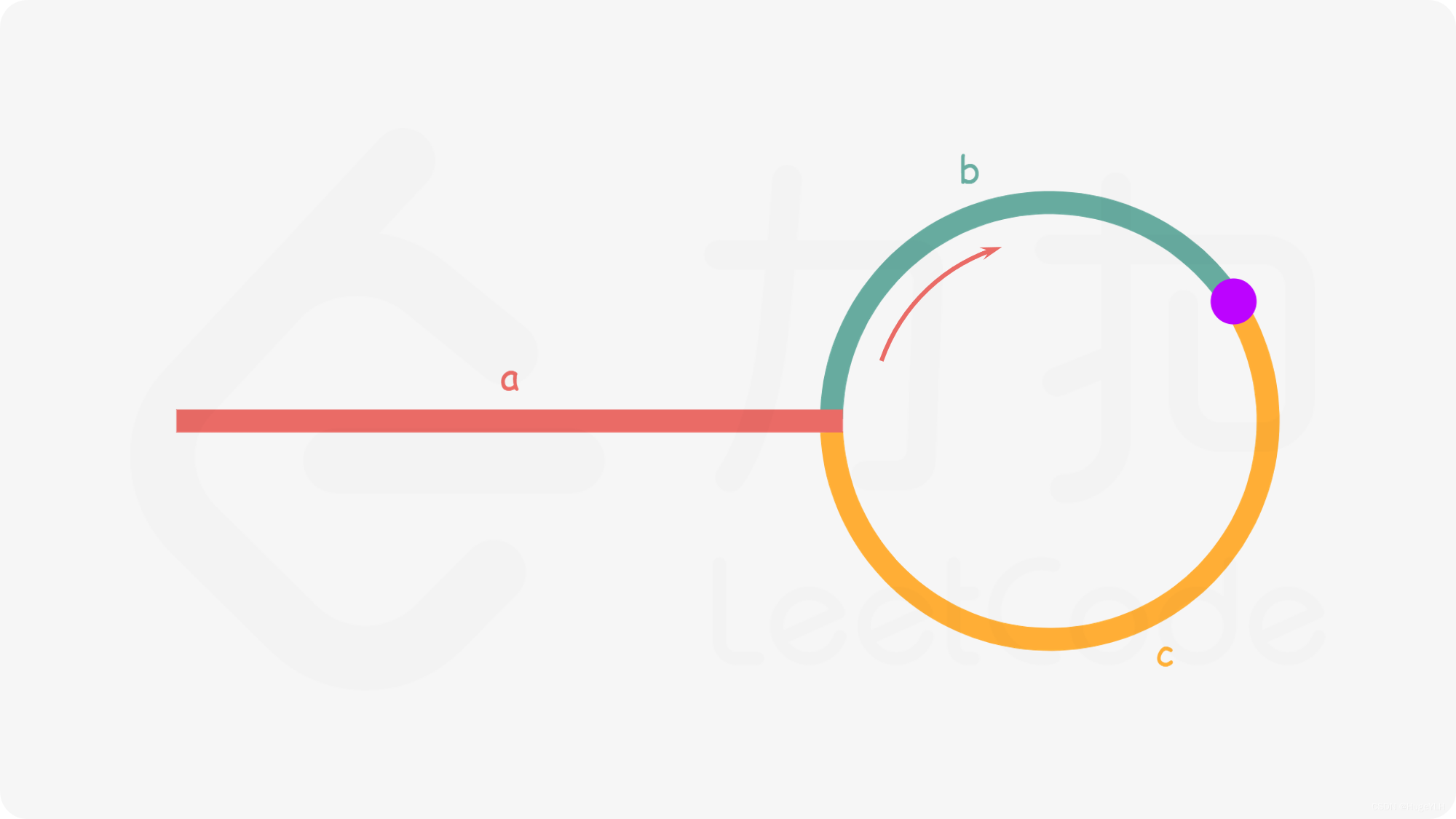
在这里插入图片描述

假设快指针和慢指针在图中圈内的紫色位置相遇。
快指针走过的路程：a + n (b + c) + b
任意时刻，快指针走的路程一定是慢指针的两倍，快指针走的路程: 2(a + b)
因此： a + n (b + c) + b = 2(a + b)
得到距离公式：a=c+(n−1)(b+c)

a=c+(n−1)(b+ c 这个公式是什么意思？？
我们把它翻译成人话：

从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。

因此当一个临时指针和慢指针同时每次走一步，slow从相遇点开始走，pTemp从链表头开始走，最后他们会同时在入口节点处相遇：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* pfast=head;
        ListNode* pslow=head;
        while (pfast!=nullptr)
        {
            pslow=pslow->next;
            if (pfast->next==nullptr)
            {
                return nullptr;
            }
            pfast=pfast->next->next;
            if (pfast==pslow)
            {
                ListNode* pTemp=head;
                while (pTemp!=pslow)
                {
                    pTemp=pTemp->next;
                    pslow=pslow->next;
                }
                return pTemp;
            }
        }
        return nullptr;
    }
};