下表1给出了近两个世纪美国人口统计表(单位:百万),建立数学模型并检验,最后用它预报2010年美国的人口。
| 年 | 1790 | 1800 | 1810 | 1820 | 1830 | 1840 | 1850 | 1860 |
| 人口 | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 |
| 年 | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 | |
| 人口 | 38.6 | 50.2 | 62.9 | 76.0 | 92.0 | 106.5 | 123.2 | |
| 年 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 | |
| 人口 | 131.7 | 150.7 | 179.3 | 204.0 | 226.5 | 251.4 | 281.4 |
1、指数增长模型(Malthus人口模型)
托马斯·罗伯特·马尔萨斯牧师(Thomas Robert Malthus,1766年2月13日-1834年12月23日)。英国教士、人口学家、经济学家。以其人口理论闻名于世。 在《人口论》(1798)中指出:人口按几何级数增长而生活资源只能按算术级数增长,所以不可避免地要导致饥馑、战争和疾病;呼吁采取果断措施,遏制人口出生率。其理论对李嘉图产生过影响 。
【模型假设】
- 人口增长率为常数
- 单位时间内人口的绝对增长与当前人口数量成正比
- 人口总数随时间连续变化
【符号说明】

【模型建立】
t时刻人口总量为x(t),对一个地区或国家来说,x(t)数量很大,视为一个可微函数。
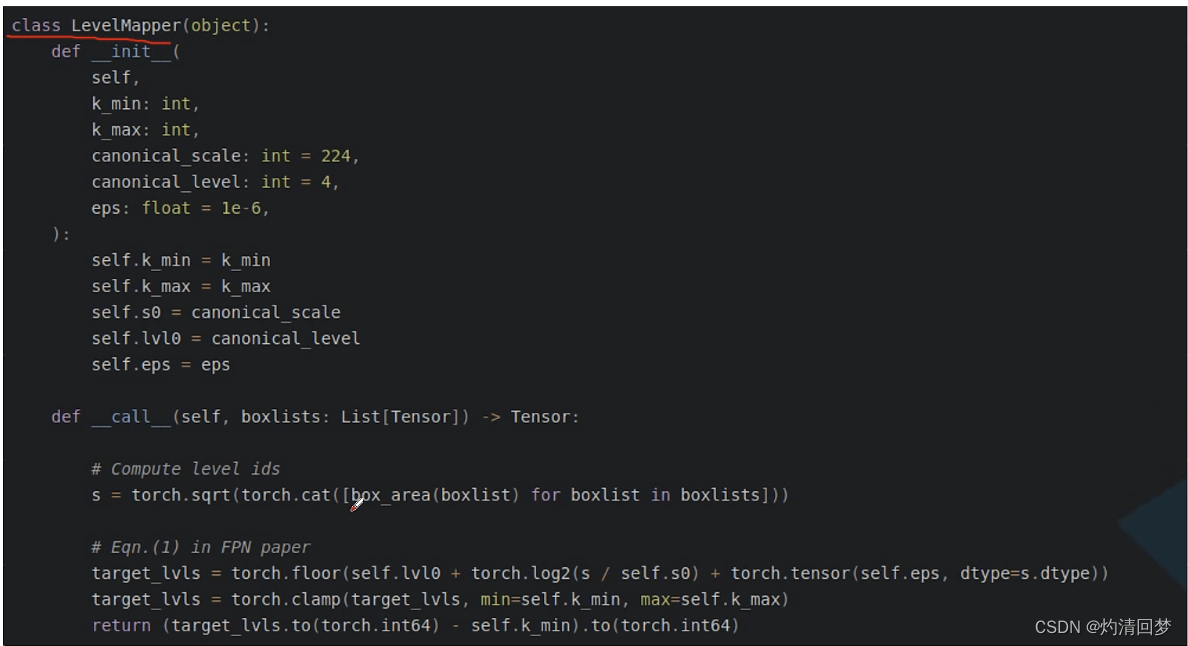
记初始时刻t=0时,人口总数为x0。根据假设(2),从t到t+Δt时间内,人口的增量正比于x(t)与Δt的乘积,即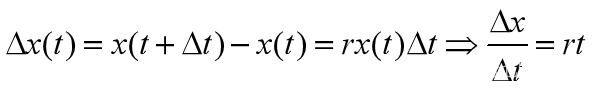
令Δt→0,得到x(t)的微分方程 【2.1】
【2.1】
变量分离容易求出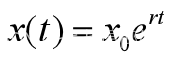 【2.2】
【2.2】
【2.2】称为指数增长模型,也称Malthus人口模型。
【参数估计】
为了更好利用表1的数据和线性拟合参数,对【2】两边取对数,有
设y=lnx,a=lnx0,则有y=a+rt【3】
这类模型的目的是为了预报预测,预测准不准确不是模型本身可以完全决定的,需要用实际数据检验。所以,在数据拟合时,一般采用前2/3的数据来拟合参数(自找导师监督学习),用后1/3的数据来检验模型的可用性。如果数据本身较少,也说明可获取的信息太少,模型的可信度本来就低。
用前12个数据,用matlab软件做直线拟合
clear
A=xlsread('d:\Arenkou.xlsx');
A=A';
t=A(:,1);x=A(:,2);
t1=t(1:12);y=log(x(1:12));
[b,bt,r,rt,st]=regress(y,[ones(length(y),1),t1]);
x0=exp(b(1));r=b(2);
得到预报公式为:
![]() 【4】
【4】
图2是前12个年份的理论值(线)与实际值(*)的对比。可以看出,这个模型基本上能够描述19世界以前美国人口增长。 这和假设(1),即人口增长率是常数基本吻合。
图2 指数增长模型拟合图 (1790-1900)
图3是全部年份的理论值(线)与实际值(*)的对比。从图可以看出,进入20世纪后,美国人口明增长变慢了,模型不再适应。 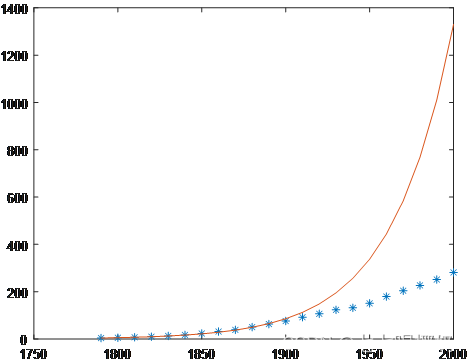
图3 指数增长模型拟合图(1790-2000)
【误差原因分析】
利用差商的形式来定义增长率,即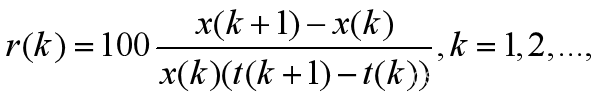 【5】
【5】
将表1中数据代入【5】,得到r(k),并绘制如图4。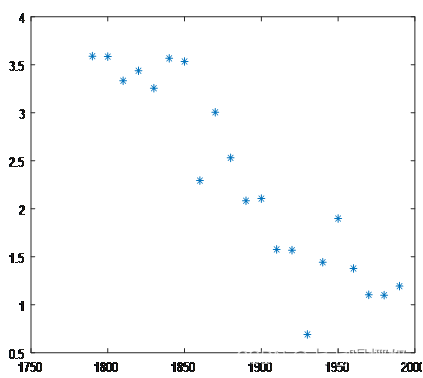
图4 时间-增长率散点图
由图4可以看出,虽然增长率是摆动的,但随着人口增长,增长率有明显的下降趋势。也可以看到,1930年左右增长率特别小(29年经济大萧条所致)。
【模型的优缺点】
1、优点
- 模型简单,易于理解和计算
- 从第一张图可以看出,Malthus人口模型在短期内拟合较好,短期预测误差不是很大
2、缺点
- 从第二张图可以看出,Malthus模型不能做中长期的预测,误差较大
- 从
看,这根本不可能,说明模型假设存在致命的缺陷。
3、修正方案
把增长率是常数修改为增长率随人口增加而降低。