1.概念
2.例题和matlab代码求解

一、概念

1.插值

（1）定义：插值是数学和统计学中的一种技术，用于估算在已知数据点之间的未知数据点的值。插值的目标是通过已知数据点之间的某种函数或方法来估计中间位置的数值。插值通常用于数据分析、图形绘制、数值模拟和其他领域。

（2）常见插值方法

1）线性插值： 是通过已知数据点之间的直线来估算中间位置的值。这意味着在两个相邻的数据点之间，估计值按照线性关系进行插值。

2）多项式插值： 使用多项式函数来逼近已知数据点。最常见的多项式插值方法是Lagrange插值和Newton插值。

3）样条插值： 将数据分段拟合成多项式，通常是低次数的多项式，以确保在相邻区间内的平滑连接。这有助于避免插值函数的过度振荡。

4）三角函数插值： 使用三角函数（如三角多项式或三角样条）来逼近已知数据点。这在周期性数据的插值中特别有用。

5）立方样条插值： 是一种非常流行的方法，它使用三次多项式在相邻数据点之间进行插值，并确保在数据点处有连续的一阶和二阶导数。这使得插值函数在插值区间内非常平滑。

补：

1.拉格朗日多项式插值是一种常用的插值方法，用于估算一组已知数据点之间的未知数据点的值。这个方法使用一个拉格朗日多项式，来逼近数据点。该多项式在每个已知数据点上都经过并且在其他点上为零。这样的多项式可以表示为：

优点是它对数据点的拟合非常精确，它会经过每个数据点。
缺点是随着数据点数量的增加，计算和插值多项式的复杂度会增加。此外，拉格朗日插值在极端情况下可能会导致插值多项式的振荡。

编写一个名为 lagrange.m 的 M 文件

function y=lagrange(x0,y0,x); 
n=length(x0);m=length(x); 
for i=1:m 
 z=x(i); 
 s=0.0; 
 for k=1:n 
 p=1.0; 
 for j=1:n 
 if j~=k 
 p=p*(z-x0(j))/(x0(k)-x0(j)); 
 end 
 end 
 s=p*y0(k)+s; 
 end 
 y(i)=s; 
end

2.牛顿插值用于估算一组已知数据点之间的未知数据点的值。这个方法使用一个牛顿多项式，来逼近数据点。该多项式在每个已知数据点上都经过，并且通过递推方式添加新的数据点来构建多项式。

牛顿插值的优点之一是它可以在添加新的数据点时轻松更新插值多项式，而不需要重新计算整个多项式。

基本步骤

牛顿插值方法通常比拉格朗日插值更有效率，因为它的计算可以逐步进行，而不需要计算大量的基函数。但与其他插值方法一样，牛顿插值的精确性也受到数据点的选择和密度的影响。

3.分段线性插值它将数据点分成若干段，并在每个段内使用线性插值来逼近数据点。这种方法通常用于处理数据在不同区间内具有不同趋势或变化的情况。分段线性插值的目标是在每个段内获得一个近似线性的插值函数，以更好地描述数据。

Matlab 中有现成的一维插值函数 interp1

 
y=interp1(x0,y0,x,'method') 

method 指定插值的方法，默认为线性插值。其值可为：
'nearest' 最近项插值
'linear' 线性插值
'spline' 逐段 3 次样条插值
'cubic' 保凹凸性 3 次插值。
所有的插值方法要求 x0 是单调的。
当 x0 为等距时可以用快速插值法，使用快速插值法的格为'*nearest'、'*linear'、'*spline'、'*cubic'。

4.Hermite 插值
如果对插值函数，不仅要求它在节点处与函数同值，而且要求它与函数有相同的一阶、二阶甚至更高阶的导数值，这就是 Hermite 插值问题。

用 Matlab 实现 Hermite 插值

function y=hermite(x0,y0,y1,x); 
n=length(x0);m=length(x); 
for k=1:m 
 yy=0.0; 
 for i=1:n 
 h=1.0; 
 a=0.0; 
 for j=1:n 
 if j~=i 
 h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; 
 a=1/(x0(i)-x0(j))+a; 
 end 
 end 
 yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i)); 
 end 
 y(k)=yy; 
end 

5.样条插值
许多工程技术中提出的计算问题对插值函数的光滑性有较高要求，如飞机的机翼外形，内燃机的进、排气门的凸轮曲线，都要求曲线具有较高的光滑程度，不仅要连续，而且要有连续的曲率，这就导致了样条插值的产生。

Matlab 中三次样条插值也有现成的函数

y=interp1(x0,y0,x,'spline')；

y=spline(x0,y0,x)；

pp=csape(x0,y0,conds)，y=ppval(pp,x)
其中 x0,y0 是已知数据点，x 是插值点，y 是插值点的函数值

对于三次样条插值，我们提倡使用函数 csape，csape 的返回值是 pp 形式，要求插值点的函数值，必须调用函数 ppval。

pp=csape(x0,y0)：使用默认的边界条件，即 Lagrange 边界条件。
pp=csape(x0,y0,conds)中的 conds 指定插值的边界条件，其值可为：
'complete' 边界为一阶导数，即默认的边界条件
'not-a-knot' 非扭结条件 
'periodic' 周期条件
'second' 边界为二阶导数，二阶导数的值[0, 0]。
'variational' 设置边界的二阶导数值为[0,0]。

对于一些特殊的边界条件，可以通过 conds 的一个1×2 矩阵来表示，conds 元素的取值为 1，2。此时，使用命令

pp=csape(x0,y0_ext,conds) 
其中 y0_ext=[left, y0, right]，这里 left 表示左边界的取值，right 表示右边界的取值。conds(i)=j 的含义是给定端点i 的 j 阶导数，即 conds 的第一个元素表示左边界的条件，第二个元素表示右边界的条件，conds=[2,1]表示左边界是二阶导数，右边界是一阶导数，对应的值由 left 和 right 给出。

详细情况请使用帮助 help csape。

2.拟合

（1）定义：拟合（Fitting）是一种数学和统计方法，用于找到一个数学模型或函数，可以最好地描述或逼近一组观测数据点。拟合的目标是找到一个函数或模型，使其与实际观测值之间的差距最小化，从而能够用来预测、分析或解释数据。

（2）常见的拟合方法

1）线性拟合： 当数据似乎遵循线性关系时，可以使用线性回归来进行拟合。线性回归寻找一条直线，使得该直线与数据点之间的残差平方和最小化。

2）多项式拟合： 多项式拟合使用多项式函数来逼近数据。可以选择不同次数的多项式来获得更高阶或更低阶的拟合。

3）非线性拟合： 当数据与非线性模型更匹配时，可以使用非线性拟合方法，例如非线性回归。这些方法尝试找到一个非线性函数，以最好地拟合数据。

4）指数拟合： 用于模拟数据遵循指数函数的情况，通常用于描述增长或衰减过程。

5）对数拟合： 适用于数据与对数函数之间的关系，通常用于分析指数增长或对数周期性数据。

6）曲线拟合： 是一种通用方法，可以拟合各种不同形状的曲线，例如正弦曲线、高斯曲线等。

7）统计拟合： 在统计学中，拟合可以使用最大似然估计或贝叶斯方法来拟合参数化模型，以最好地描述观测数据的分布。

8）核心拟合： 在机器学习和模式识别中，核心方法（如支持向量机）可用于拟合数据并生成分类或回归模型。

补：

1.线性最小二乘法（Linear Least Squares Method）是一种常用的统计和数学方法，用于拟合一个线性模型，以最小化观测数据点与模型预测值之间的残差平方和。这个方法通常用于回归分析，其中目标是找到一个线性模型，以最好地描述因变量和自变量之间的关系。

二、例题

1 机床加工
待加工零件的外形根据工艺要求由一组数据(x, y) 给出（在平面情况下），用程控铣床加工时每一刀只能沿 x 方向和 y 方向走非常小的一步，这就需要从已知数据得到加工所要求的步长很小的(x, y) 坐标。表 1 中给出的 x, y 数据位于机翼断面的下轮廓线上，假设需要得到 x 坐标每改变0.1 时的 y 坐标。试完成加工所需数据，画出曲线，并求出 x = 0 处的曲线斜率和13 ≤ x ≤ 15 范围内 y 的最小值。

要求用 Lagrange、分段线性和三次样条三种插值方法计算。

matlab代码需要用到之前写好的函数调用

clc,clear 
x0=[0 3 5 7 9 11 12 13 14 15]; 
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6]; 
x=0:0.1:15; 
y1=lagrange(x0,y0,x); %调用前面编写的Lagrange插值函数
y2=interp1(x0,y0,x); 
y3=interp1(x0,y0,x,'spline'); 
pp1=csape(x0,y0); y4=ppval(pp1,x); 
pp2=csape(x0,y0,'second'); y5=ppval(pp2,x); 
fprintf('比较一下不同插值方法和边界条件的结果:\n') 
fprintf('x y1 y2 y3 y4 y5\n') 
xianshi=[x',y1',y2',y3',y4',y5']; 
fprintf('%f\t%f\t%f\t%f\t%f\t%f\n',xianshi') 
subplot(2,2,1), plot(x0,y0,'+',x,y1), title('Lagrange') 
subplot(2,2,2), plot(x0,y0,'+',x,y2), title('Piecewise linear') 
subplot(2,2,3), plot(x0,y0,'+',x,y3), title('Spline1') 
subplot(2,2,4), plot(x0,y0,'+',x,y4), title('Spline2') 
dyx0=ppval(fnder(pp1),x0(1)) %求x=0处的导数
ytemp=y3(131:151); 
index=find(ytemp==min(ytemp)); 
xymin=[x(130+index),ytemp(index)]

例2 在一丘陵地带测量高程，x 和 y 方向每隔100米测一个点，得高程如2表，试插
值一曲面，确定合适的模型，并由此找出最高点和该点的高程。

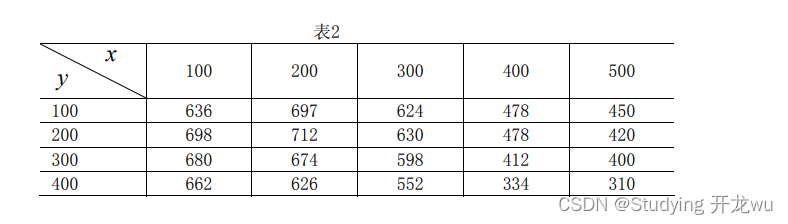
clear,clc 
x=100:100:500; 
y=100:100:400; 
z=[636 697 624 478 450 
 698 712 630 478 420 
680 674 598 412 400 
 662 626 552 334 310]; 
pp=csape({x,y},z') 
xi=100:10:500;yi=100:10:400 
cz1=fnval(pp,{xi,yi}) 
cz2=interp2(x,y,z,xi,yi','spline') 
[i,j]=find(cz1==max(max(cz1))) 
x=xi(i),y=yi(j),zmax=cz1(i,j)

例 3 在某海域测得一些点（x,y）处的水深 z 由下表给出，在矩形区域（75,200）
×(-50,150) 内画出海底曲面的图形。

x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5]; 
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5]; 
z=-[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
xi=75:1:200; 
yi=-50:1:150; 
zi=griddata(x,y,z,xi,yi','cubic') 
subplot(1,2,1), plot(x,y,'*') 
subplot(1,2,2), mesh(xi,yi,zi) 

例4 用最小二乘法求一个形如 y = a + bx^2 的经验公式，使它与表 4 所示的数据
拟合

x=[19 25 31 38 44]'; 
y=[19.0 32.3 49.0 73.3 97.8]'; 
r=[ones(5,1),x.^2]; 
ab=r\y 
x0=19:0.1:44; 
y0=ab(1)+ab(2)*x0.^2; 
plot(x,y,'o',x0,y0,'r') 

例 5 某乡镇企业 1990-1996 年的生产利润如表 5,试预测 1997 年和 1998 年的利润。

编写程序如下：

x0=[1990 1991 1992 1993 1994 1995 1996]; 
y0=[70 122 144 152 174 196 202]; 
a=polyfit(x0,y0,1) 
y97=polyval(a,1997) 
y98=polyval(a,1998) 

求得 a1 = 20，a0 = −4.0705×10 ，
1997 年的生产利润 y97=233.4286，1998 年的生产利润 y98=253.9286。